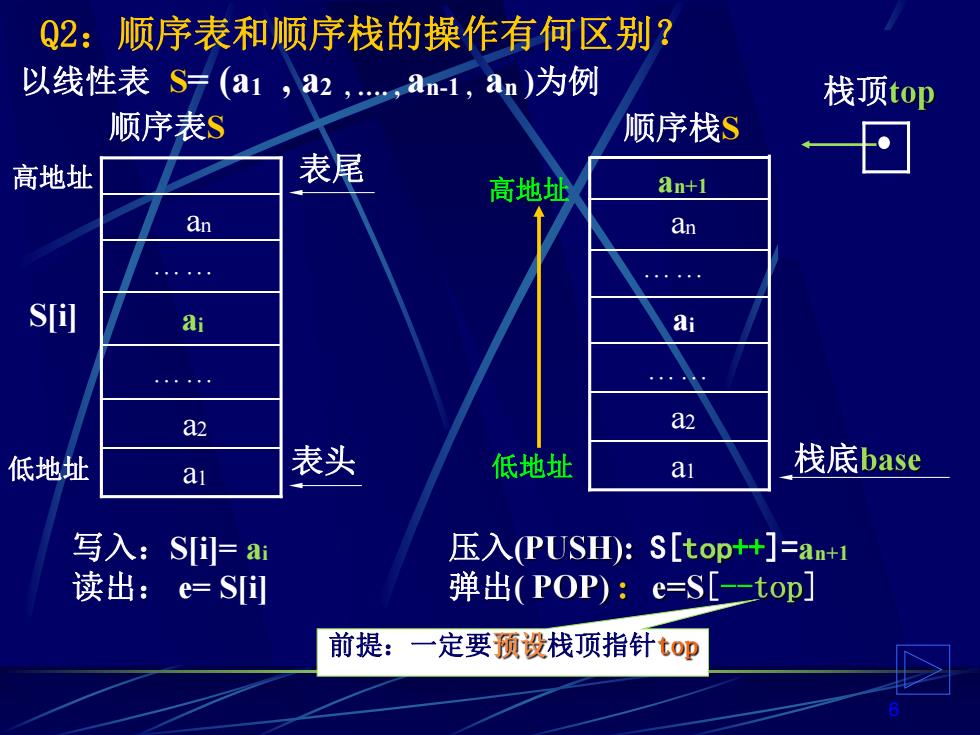
Q2:顺序表和顺序栈的操作有何区别? 以线性表S(a,a2,an-1,an)为例 栈顶top 顺序表S 顺序栈S 高地址 表尾 高地址 an+1 an an · S ai ai 。., a2 a2 低地址 a 表头 低地址 ai 栈底base 写入:S=ai 压入PUSD:S[topt+]=an+1 读出:e=S] 弹出(POP):e=S[-二top] 前提:一定要预设栈顶指针top
6 a1 a2 . an 顺序栈S ai . Q2:顺序表和顺序栈的操作有何区别? 表头 表尾 低地址 高地址 写入:S[i]= ai 读出: e= S[i] 压入( S[ ++]=an+1 弹出( [- ] 低地址 高地址 S[i] a1 a2 ai an . 顺序表S . an+1 以线性表 S= (a1 , a2 , . , an-1 , an )为例 栈底 栈顶 前提:一定要 栈顶指针 栈顶
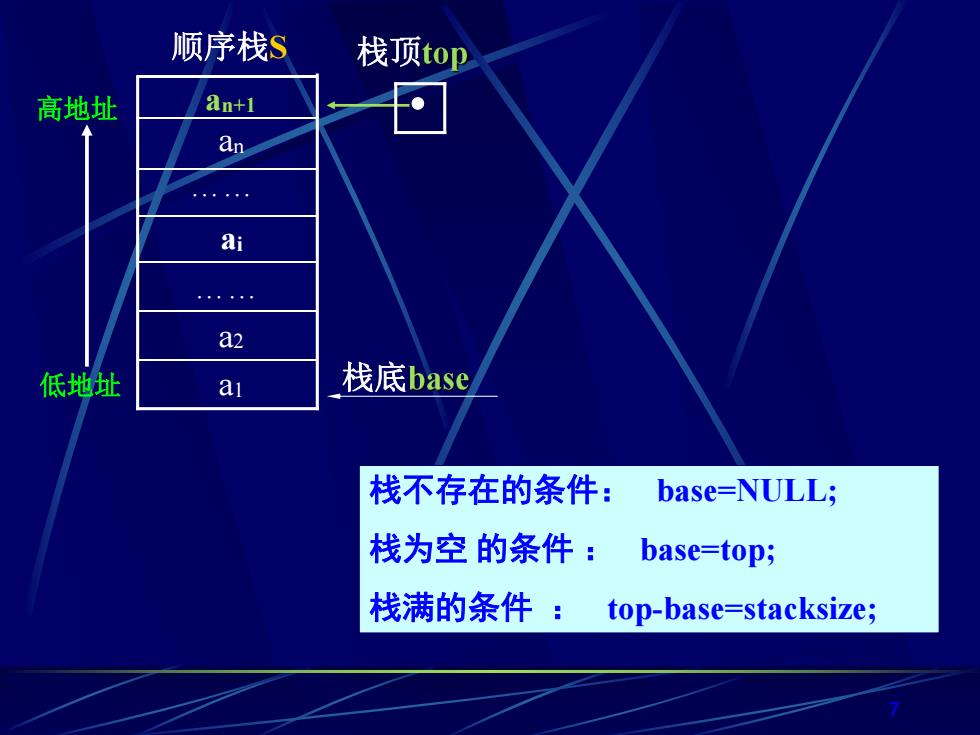
顺序栈S 栈顶top 高地址 an+1 an ai a2 低地址 ai 栈底base 栈不存在的条件: base=NULL; 栈为空的条件:base=top; 栈满的条件:top-base=stacksize;
7 栈不存在的条件: base=NULL; 栈为空 的条件 : base=top; 栈满的条件 : top-base=stacksize; a1 a2 . an 顺序栈S ai . 低地址 高地址 an+1 栈底 栈顶

Q3:什么叫“向上生成”的栈?“向下生成”又是何 意? 若入栈动作使地址向高端增长,称为“向上生成”的栈; 若入栈动作使地址向低端增长,称为《向下生成”的栈; 对于向上生成的堆栈: 入栈口诀:堆栈指针top“先压后加”:S[top+]=ant1 出栈口诀:堆栈指针top“先减后弹”:e=S[top]
8 若入栈动作使地址向高端增长,称为“向上生成”的栈; 若入栈动作使地址向低端增长,称为“向下生成”的栈; 对于向上生成的堆栈: 入栈口诀:堆栈指针top “先压后加” : S[top++]=an+1 出栈口诀:堆栈指针top “先减后弹” : e=S[-top] Q3:什么叫“向上生成”的栈? “向下生成”又是何 意?

Q4:为什么要设计堆栈?它有什么独特用途? 调用函数或子程序非它莫属; 2. 递归运算的有力工具; 3.用于保护现场和恢复现场: 4.简化了程序设计的问题。 下面用4个例子来帮助理解堆栈:
9 Q4:为什么要设计堆栈?它有什么独特用途? 1. 调用函数或子程序非它莫属; 2. 递归运算的有力工具; 3. 用于保护现场和恢复现场; 4. 简化了程序设计的问题。 下面用4个例子来帮助理解堆栈:
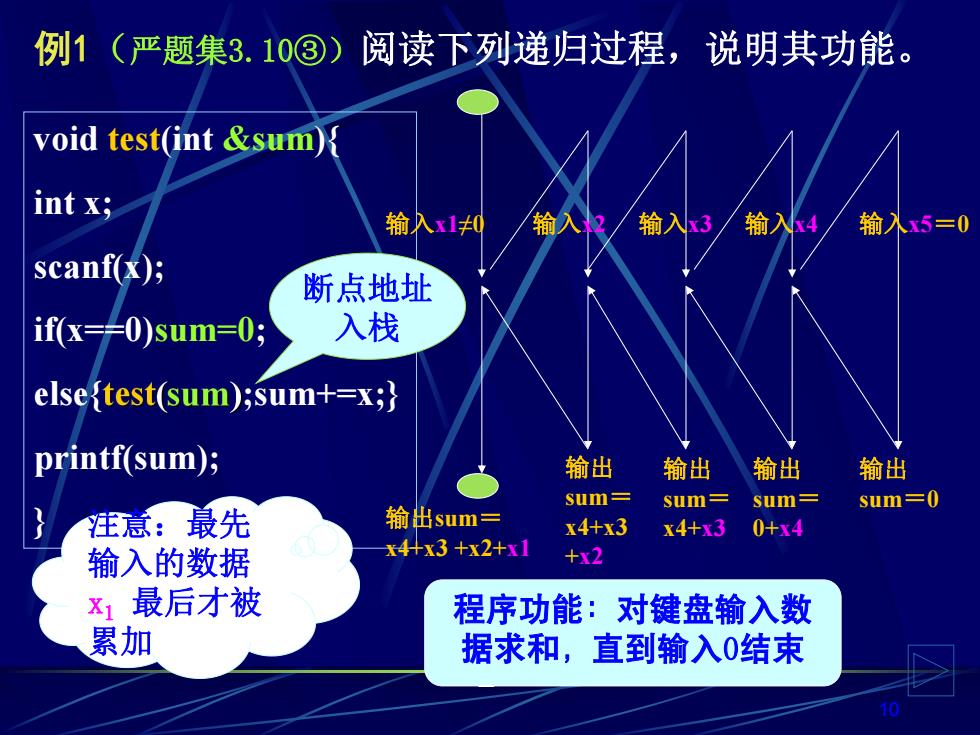
例1(严题集3.10③)阅读下列递归过程,说明其功能。 void test(int &sum) int x; 输入x10 输入权/输入3/输入4 输入x5=0 scanf(x); 断点地址 if(x=≠0)sum=0; 入栈 elseftest(sum);sum+=x;} printf(sum); 输出 输出 输出 输出 sum= 输出sum三 sum= sum= sum=0 注意:最先 x4+x3 x4+x30+x4 输入的数据 x4+x3+x2+x1 +x2 x1最后才被 程序功能:对键盘输入数 累加 据求和,直到输入0结束
10 void test(int &sum){ int x; scanf(x); if(x==0)sum=0; else{ ;sum+=x;} printf(sum); } 断点地址 入栈 例1(严题集3.10③)阅读下列递归过程,说明其功能。 输入x1≠0 输入x2 输入x3 输入x4 输入x5=0 输出 sum=0 输出 sum= 0+x4 输出 sum= x4+x3 输出 sum= x4+x3 +x2 输出sum= x4+x3 +x2+x1 注意:最先 输入的数据 x1 最后才被 累加 程序功能:对键盘输入数 据求和,直到输入0结束