
第10章内邰排序 10.1概述 10.2插入排序 10.3交换排序 10.4选择排序 10.5归并排序 10.6基数排序 附:各种内部排序方法的比较
1 10.1 概述 10.2 插入排序 10.3 交换排序 10.4 选择排序 10.5 归并排序 10.6 基数排序 第10章 内部排序 附:各种内部排序方法的比较

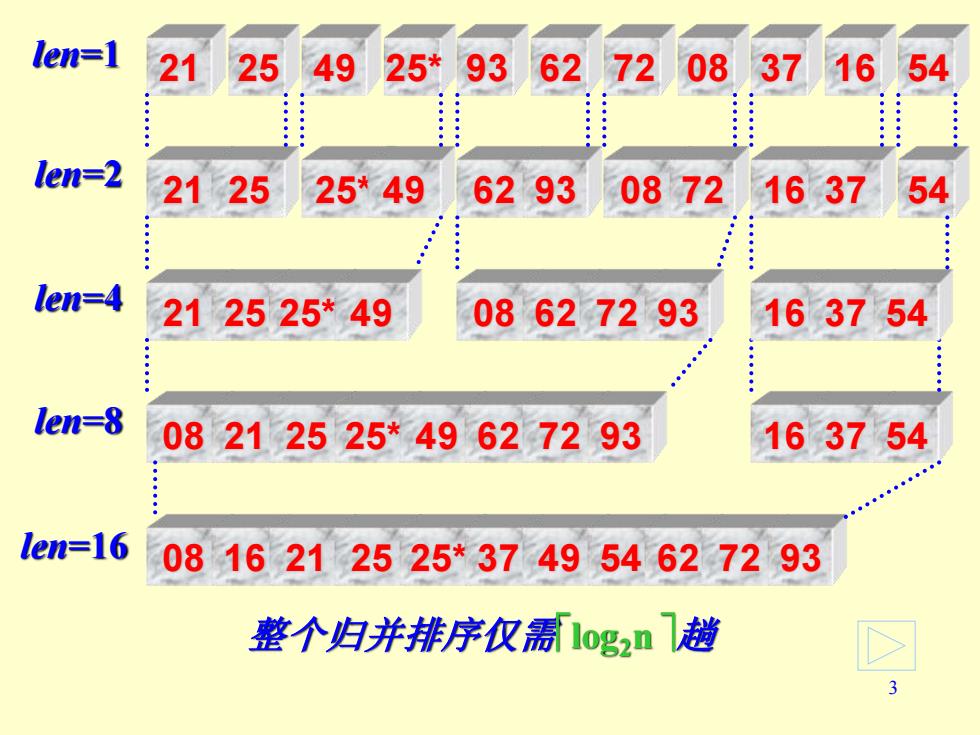
10.5归并排序 归并排序的基本思想是:将两个(或以上)的有序 表组成新的有序表。 更实际的意义:可以把一个长度为n的无序序列看成是n个 长度为1的有序子序列,首先做两两归并,得到「n/21个 长度为2的有序子序列:再做两两归并,.,如此重复, 直到最后得到一个长度为的有序序列。 例:关键字序列T=(21,25,49,25*,93,62, 72,08,37,16,54),请给出归并排序的具体实 现过程
2 10.5 归并排序 归并排序的基本思想是:将两个(或以上)的有序 表组成新的有序表。 更实际的意义:可以把一个长度为n 的无序序列看成是 n 个 长度为 1 的有序子序列 ,首先做两两归并,得到 n / 2 个 长度为 2 的有序子序列 ;再做两两归并,.,如此重复, 直到最后得到一个长度为 n 的有序序列。 例:关键字序列T= (21,25,49,25* ,93,62, 72,08,37,16,54),请给出归并排序的具体实 现过程
len=1 21 2549 25*93 62 72 08 37 16 54 len=2 2125 25*49 6293 0872 1637 len=4 212525*49 08627293 163754 len=8 08212525*49627293 163754 len=16 0816212525*374954627293 整个归并排序仅需10g2n1趟
3 21 25 49 25* 93 62 72 08 37 16 54 21 25 25* 49 62 93 08 72 16 37 54 16 37 54 21 25 25* 49 08 62 72 93 08 21 25 25* 49 62 72 93 08 16 21 25 25* 37 49 54 62 72 93 len=1 len=2 len=4 len=8 len=16 16 37 54 整个归并排序仅需log2n 趟

一趟归并排序算法:(两路有序并为一路) 参见救材P283 void Merge (SR,&TR,i,m,n) ∥将有序的SR[i.m和SRm+1.归并为有序的TR[i.n for(k=i,j=m+1;i<=m &&j<=n;++k){ if (SR[i]<=SR[j])TR[k]=SR[i++]; else TR[k=SR+;∥将两个SR记录由小到大并入TR }∥for f(=m)TRk.n=SRi.m;∥将剩余的SR[i.m复制到TR if(G=n)TRk.=SRj.n;∥将剩余的SRj.复制到TR }∥Merge 这就是能提高排 序速度的原因
4 一趟归并排序算法: (两路有序并为一路) 参见教材P283 void Merge (SR,&TR,i, m, n) { // 将有序的SR[i.m]和SR[m+1.n]归并为有序的TR[i.n] for(k=i , j=m+1; i<=m && j<=n; ++k ) { if ( SR[i]<= SR[j] )TR[k]=SR[i++]; else TR[k]=SR[j++]; // 将两个SR记录由小到大并入TR } // for if (i<=m) TR[k.n]=SR[i.m]; // 将剩余的SR[i.m]复制到TR if (j<=n) TR[k.n]=SR[j.n]; // 将剩余的SR[j.n]复制到TR } // Merge 这就是能提高排 序速度的原因

递归形式的两路归并完整排序算法: :参见材P284 void MSort(SR[],&TR1】,s,){∠初次调用时为(L,L,l,length) /将无序的SRs.归并排序为TR1s. if(s=t)TR1s=SRs;∥当len=1时返▣ else m=(s+t)/2;∥将SR[s.t平分为SR[s.m和SR[m+1.) MSot(SR,&TR2,S,m);∥将SR一分为二,2分为4. /∥递归地将SRs.m归并为有序的TR2[s.m MSort (SR &TR2,m+1,t); ∥递归地将SR[m+1.归并为有序的TR2[m+1.) Merge(TR2,TR1,s,m,t); /将TR2[s.m和TR2m+1.t归并到TR1[s.t //if }I∥MSort 简言之,先由“长”无序变成“短”有序 再从“短”有序归并为“长”有序
5 if ( s==t )TR1[s]=SR[s]; // 当len=1时返回 else { } //if } // MSort m=(s+t)/2; // 将SR [s.t]平分为SR [s.m]和SR [m+1.t] MSort (SR,&TR2,s, m); // 将SR 一分为二, 2分为4. // 递归地将SR [s.m]归并为有序的TR2[s.m] MSort (SR,&TR2,m+1, t ); // 递归地将SR [m+1.t]归并为有序的TR2[m+1.t] Merge(TR2, TR1, s, m, t ); // 将TR2 [s.m]和TR2 [m+1.t]归并到TR1 [s.t] void MSort (SR[ ],&TR1[ ],s, t) { // 将无序的SR[s.t]归并排序为TR1[s.t] 递归形式的两路归并完整排序算法: 参见教材P284 简言之,先由“长”无序变成“短”有序, 再从“短”有序归并为“长”有序。 初次调用时为(L, L, 1, length)