
基本理论 二、原子吸收光谱的特性一吸收线的轮廓 自然宽度(Natural Width) 激发态原子寿命(105nm) 多普勒变宽(Doppler Broadening) 一原子的无序运动(热变宽) 劳伦兹变宽(Lorentz Broadening) 一原子与其他原子或分子之间的相互碰撞 12
12 自然宽度(Natural Width Natural Width) —— 激发态原子寿命(10 —— -5 nm) 多普勒变宽(Doppler Broadening Doppler Broadening) —— 原子的无序运动(热变宽) —— 劳伦兹变宽 (Lorentz Lorentz Broadening Broadening) —— 原子与其他原子或分子之间的相互碰撞 二、原子吸收光谱的特性 二、原子吸收光谱的特性 --吸收线的轮廓 基本理论
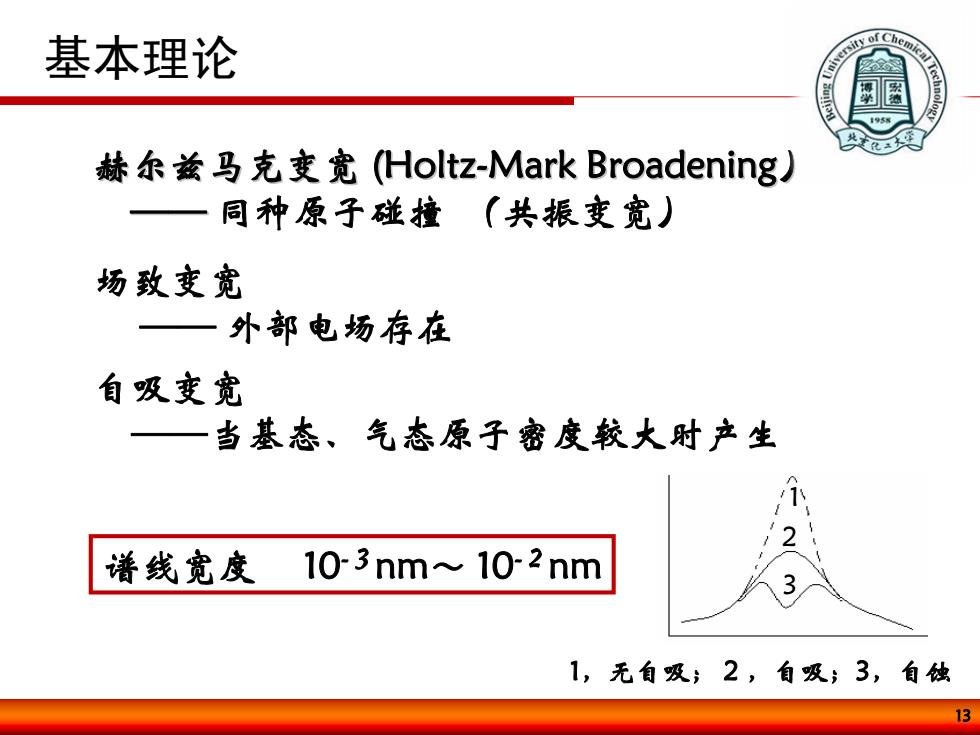
基本理论 sity of C 9 赫尔兹马克变宽(Holtz-Mark Broadening.) 一同种原子碰撞(共振变宽) 场致变宽 一外部电场存在 自吸变宽 一当基态、气态原子密度较大时产生 谱线宽度103nm~102nm 3 1,无自吸;2,自吸;3,自烛 13
13 赫尔兹马克变宽 赫尔兹马克变宽 (Holtz-Mark Broadening Mark Broadening) —— 同种原子碰撞 (共振变宽) —— 场致变宽 —— 外部电场存在 谱线宽度 10-3nm~ 10-2nm 基本理论 自吸变宽 ——当基态、气态原子密度较大时产生 1 2 3 1,无自吸; 2 ,自吸;3,自蚀

基本理论 y of Che 图 化因 三、原子吸收值与原子浓度之间的关集 朗伯一比耳定律 积分吸收 多峰值吸收
14 三、原子吸收值与原子浓度之间的关系 三、原子吸收值与原子浓度之间的关系 基本理论 朗伯—比耳定律 积分吸收 峰值吸收
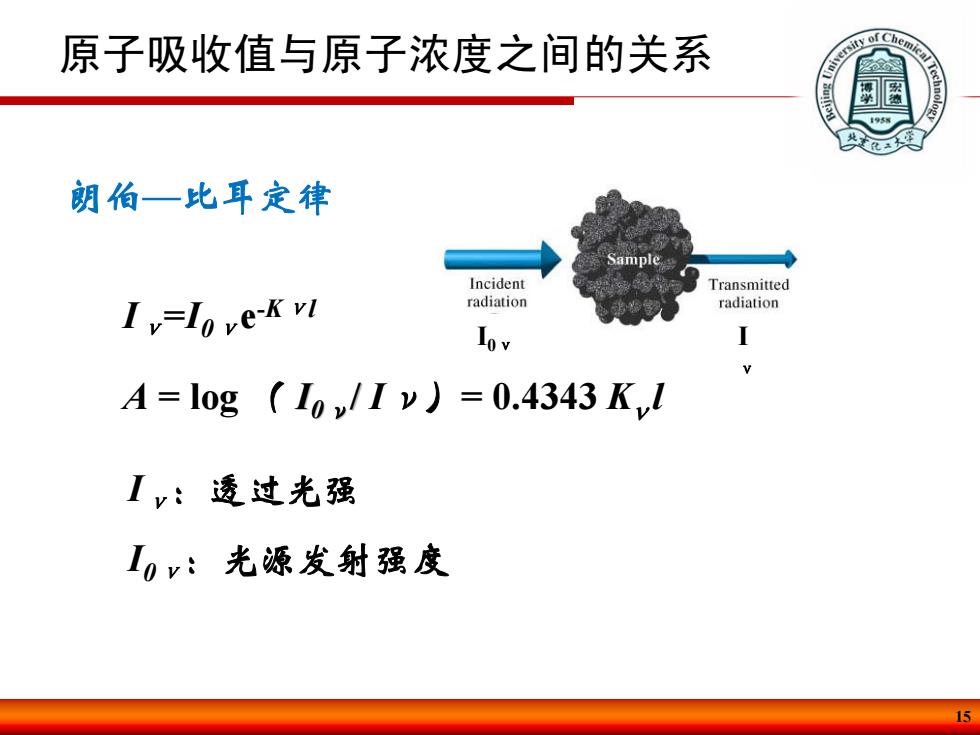
原子吸收值与原子浓度之间的关系 sity of C 朗伯—比耳定律 Incident Transmitted Iv=loveK vi radiation radiation Iov A=log (I,/Iv)=0.4343 K,I Iy:透过光强 I,v:光源发射强度
15 原子吸收值与原子浓度之间的关系 朗伯 —比耳定律 I ν =I0 ν e -K ν l A = log ( I0 ν/ I ν )= 0.4343 Kνl I ν:透过光强 I0 ν:光源发射强度 I 0 ν I ν

原子吸收值与原子浓度之间的关系 y of Ce 图 积分吸收 e。电子电荷m-电子质量 C-光速f-振子强度 八o单位体积原子蒸气中基态原子数 ∫Kd=(πe2lmc)fNov NovN总 K ∫Kdv=KN 6
16 原子吸收值与原子浓度之间的关系 积分吸收 e - 电子电荷 m –电子质量 c – 光速 f – 振子强度 N0ν - 单位体积原子蒸气中基态原子数 ∫ Kνd ν=( π e 2 /mc ) ƒN0 ν N0 ν=N总 ∫ Kνd ν = KN