
failure is: failure is: For failure by the transverse tensile stress, For failure by the longitudinal compressive stress, calculations are now as follows: t话话。5(0) EXAMPLE 4.2 failure is: 1P-44.3M2a So the corresponding off-axis shear stress required to produce this mode of 025270008941m0-27000945·54m45-79:50-4482Pa 10-1443M29 So the corresponding off-axis shear stress required to produce this mode of G1-279080800-27000845.8m45--70-850--1448.vea Criterion,along with the strength data for T300/5208 from table 4.1,the cipal material axes.Employing equation(2.31)and the Maximum Stress produces longitudinal compression and transverse tension along the prin- Solution.From figure 4.5(b),it is seen that a negative off-axis shear stress Repeat example 4.1 if the off-axis shear stress in example 4.1 is negative,as shown 101248M1a of the off-axis shear stress required to produce failure is: So transverse compression is the governing mode of failure,and the value Tn2 =Tx(cos20-sin20)=txy (cos245-sin2 45")=0 There is no shear stress along the principal material axes,since Txy =248MPa So the corresponding off-axis shear stress required to produce this mode of Principles of Composite Material Mechanics satisfied: strain relationships in equation (2 241rith. shear strain Y2. failure stress. now only skewed parallelogram,as shown in figure 4.2 and figure 4.3.The shape of the parallelogram can be deduced by combining the lamina stress- similar to that of the Maximum Stress Criterion in o1-02 space.In 01-02 space,however,the Maximum Strain Criterion failure surface is a surface for the Maximum Strain Criterion in e1-E2 space is a rectangle Due to the similarity of equation(4.5)and equation(4.2),the failure failure along the principal material axes is independent of the sign of the (4.1).As with the Maximum Stress Criterion,it is assumed that shear where the numerical values of e)and e)are assumed to be positive and the ultimate strains are all engineering strains as defined by equation -et)<e<e) according to this criterion,the following set of inequalities must be rion predicts failure when any principal material axis strain component exceeds the corresponding ultimate strain.In order to avoid failure discussed in elementary mechanics of materials courses [251.This crite- Theory (or Saint Venant's Theory)for isotropic materials,which is also In 1967,Waddoups [29]proposed the Maximum Strain Criterion for orthotropic laminae as an extension of the Maximum Normal Strain 4.2.2 Maximum Strain Criterion negative produces a completely different mode of failure and a much lower So simply changing the sign of the off-axis shear stress from positive to T-44329 So transverse tension is now the governing mode of failure,and the corre- sponding value of the off-axis shear stress required to produce failure is t5-t0o0820-51m200-78C0s:430-8m2450-0 Again there is no shear stress along the principal material axes,since Strength of a Continuous Fiber-Reinforced Lamina 三

simple. 1 direction is and maximum strain criteria in that they include terms to account for theories for isotropic materials,but they differ from the maximum stress The so-called quadratic interaction criteria also evolved from early failure 4.2.3 Quadratic Interaction Criteria for orthotropic materials because the resulting equations are relatively data have led to similar conclusions [28],but both criteria are still used biaxial failure data for graphite/epoxy in figure 4.3.Off-axis uniaxial test dicted failure surface does not show good agreement with experimental account for possible interaction between stress components,and the pre- Maximum Stress Criterion,the Maximum Strain Criterion does not same for the maximum stress and maximum strain criteria.As with the are satisfied.Only for isotropic materials are the intercepts always the to stress space unless certain mathematical constraints on the properties tions develop as a result of an ambiguous conversion from strain space tradicts experimental evidence [5,8].According to Wu [5],such contradic- the measured tensile and compressive longitudinal strengths,which con- Criterion parallelogram intercept the horizontal axis at stresses less than rials,the lines defining the top and bottom of the Maximum Strain of the Maximum Stress Criterion rectangle in stress space.For some mate- Maximum Strain Criterion parallelogram may not be the same as those nitudes of the lamina strengths and stiffnesses,the intercepts of the ing two sides.It should be noted,however,that depending on the mag- strains in the negative 1 and 2 directions yields equations for the remain- ogram shown in figure 4.2,and similar consideration of the limiting va These lines form the right and top sides,respectively,of the parallel- which is the equation for a straight line having intercept(0,s))and slope 21801483 positive 2 direction yields the equation: 1/v12(fig.4.2).A similar development using the limiting strain along the which is the equation of a straight line having intercept(sL(),0)and slope 9/ V12 9 equation(4.1).For example,the limiting strain associated with the positive Principles of Composite Material Mechanics 多 S assumed to be the same.Solving equation(4.10)and equation(4.11)simul- taneously for A,B,and C,we find that tions,respectively.The yield strengths in tension and compression are where Y2 and Y3 are the uniaxial yield strengths along the 2 and 3 direc- along the 2 and 3 directions give the equations where Yi is the yield strength along 1 direction.Similarly,uniaxial tests to zero equation(4.9)reduces to: uniaxial test along the 1 direction with o1=Yi and all other stresses equal (4.9)must be <1,and failure is predicted if the left-hand side is 21.For a or shear loading.In order to avoid failure,the left-hand side of equation where A,B,C,D,E,and F are determined from yield strengths in uniaxial A(62-G3)2+B(03-G1)2+C(01-02)2+2Dt+2Et3+2Fti=1 (4.9) the Hill Criterion in o02,and o3 space is described by the equation: three-dimensional state of stress along the principal axes of anisotropy (the 123 axes)in such a material,the failure surface (or yield surface)for could be modified to include the effects of induced anisotropic behavior in initially isotropic metals during large plastic deformations.For a general quadratic interaction criteria for predicting the onset of yielding in iso- tropic metals [25].In 1948,Hill [30]suggested that the von Mises Criterion in any mechanics of materials book,the maximum distortional energy criterion or von Mises Criterion(circa early 1900s)is the most widely used the equations for plane stress lead to elliptical failure surfaces.As shown interaction between the stress components,and the quadratic forms of Strength of a Continuous Fiber-Reinforced Lamina 412 (410

stress space. 40080n6s: the prediction of yielding in ductile metals,the equations are based on Since the von Mises and Hill Criteria are phenomenological theories for interaction criteria based on the von Mises model,there is another problem. In addition to the previously mentioned limitations of the quadratic 2,and oa,as suggested by Hoffman [33] compression is to include terms that are linear in the normal stresses ou One way to account for different strengths in tension and well for the graphite/epoxy material except for the fourth quadrant of [25,32].As shown in figure 4.3,the procedure seems to work reasonably Mises and Hill Criteria,it has been successfully used for some composites is inconsistent with the assumptions used in formulating the original von for the case of graphite/epoxy in figure 4.3.Although such a procedure resulting failure surface is no longer symmetric about the origin,as shown negative,the values of sL()and s)would be used in equation (4.14).The for each quadrant of stress space.For example,if o is positive and o2 is strengths are different by simply using the appropriate value of st and sr The Tsai-Hill equation can be used when tensile and compressive because of the assumption of equal strengths in tension and compression. figure 4.2.The ellipse shown in figure 4.2 is symmetric about the origin The.failure surface generated by this equation is an ellipse,as shown in equation(4.14)is <1,and failure is predicted if the left-hand side is 2L As with the Hill equation,failure is avoided if the left-hand side of for the Tsai-Hill failure surface: 9 三、+元⊙ equation(4.9),equation(4.12),and equation(4.13)reduce to the equation effective lamina strengths,then Y1=sL Y2=Y3 =sp and Y12=sLp and and if Hill's anisotropic yield strengths are replaced by the corresponding the reinforcement direction,if plane stress is assumed (03=31=723=0), axes of the transversely isotropic lamina,with the 1 direction being along Criterion.If the 123 directions are assumed to be the principal material and Tsai [32];the resulting equation is often referred to as the Tsai-Hill tropic,transversely isotropic lamina was suggested by Azzi and Tsai [31] The extension of the Hill Criterion to prediction of failure in an ortho- 12,23,and 31 planes,respectively. where Yi2,Y2s,and Ys are the yield strengths in shear associated with the Similarly,for pure shear tests along the 23,31,and 12 planes,equation Principles of Composite Material Mechanics (4·13 am neous solution of the two equations resulting from equation(4.16)yields: of the uniaxial and shear strengths using the same approach that was used with the Hill Criterion.For example,for the tension and compression tests with uniaxial stresses 01=s()and o1=sL,respectively,simulta- of F,all the strength tensors in equation(4.16)can be expressed in terms strengths in tension and compression.In addition,the term 2F120102 takes into account interaction between the normal stresses.With the exception stress 0.remains.However,the linear terms in the normal stresses o1=ou and 02=022 are retained because they take into account the different because the shear strength along the principal material axes is not affected by the sign of the shear stress.Thus,only a quadratic term in the shear where the linear terms in the shear stress 0o=t12 have been dropped Fi+F202+F660+F01+F202+2F20102=1 For the case of plane stress with 03=0a3=0,0=T23=0,and os=T1=0, equation (4.15)becomes (4.15)must be <1,and failure is predicted when the left-hand side is 21. experimentally determined strength tensors of the second and fourth rank,respectively.In order to avoid failure,the left-hand side of equation where the contracted notation i,j=1,2,...,6 is used,and Fi and Fi are described by the tensor polynomial: Foi+Fojoj=1 been suggested earlier by Gol'denblat and Kopnov [35].In the Tsai-Wu general quadratic interaction criteria,the failure surface in stress space is of a tensor polynomial failure theory for anisotropic materials that had quadratic interaction criterion,which will be discussed next. In 1971,Tsai and Wu [34]proposed an improved and simplified version However,all of these theories turn out to be special cases of a more general of its linear terms,could predict failure for the hydrostatic state of stress. can produce shear strains and failure.Hoffman's equation [33],by virtue hydrostatic state of stress o1=02=03,and 2=23=T1=0.Due to shear coupling,however,a hydrostatic state of stress in an anisotropic material ing,and the Hill Criterion predicts that failure will never occur under a cause the slip and dislocation movements that are associated with yield- Experimental evidence suggests that a hydrostatic state of stress does not principal stress differences and the corresponding shear stresses and strains that drive slip and dislocation movement in metallic crystals. Strength of a Continuous Fiber-Reinforced Lamina (413 416 (415
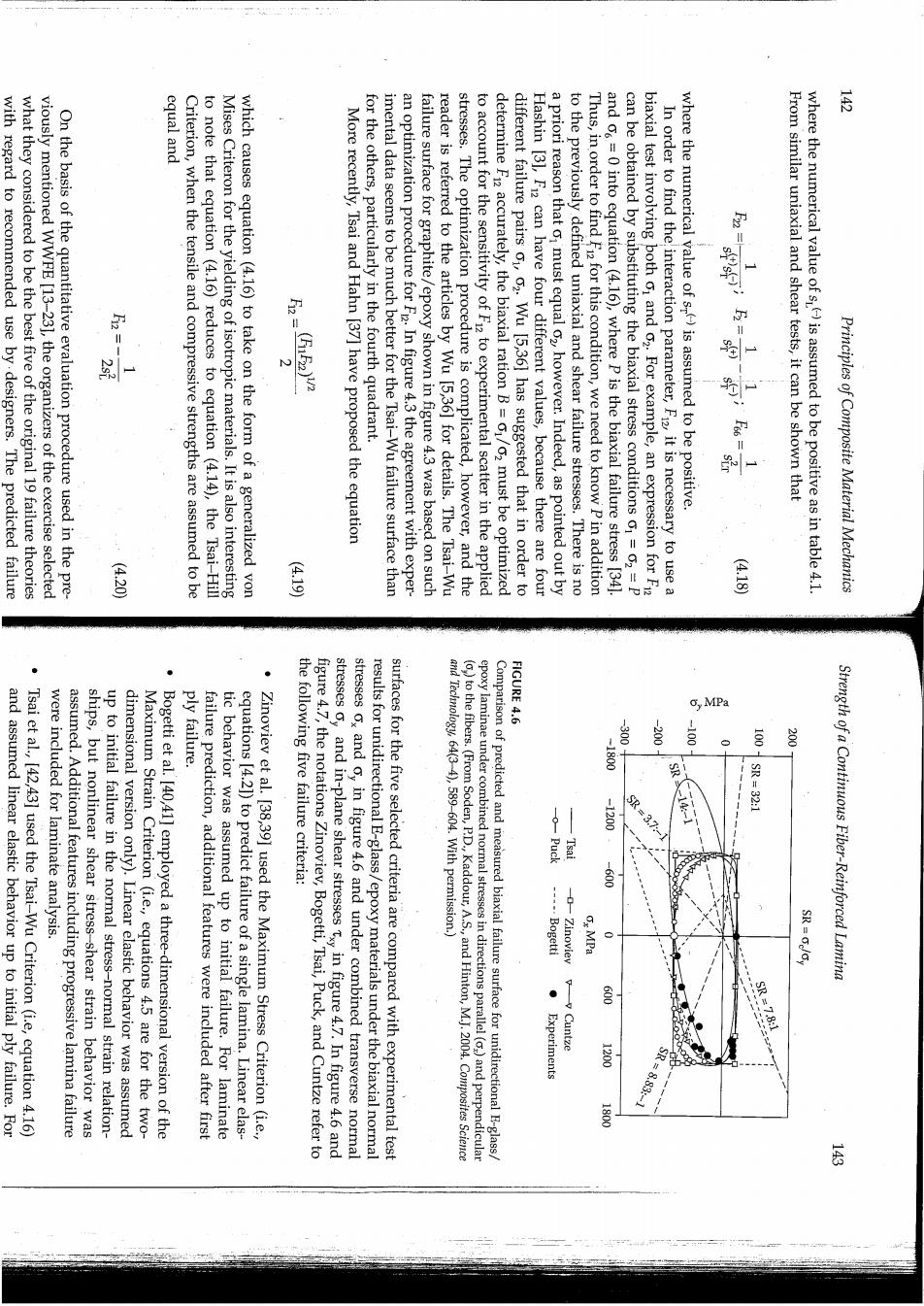
equal and with regard to recommended use by.designers.The predicted failure what they considered to be the best five of the original 19 failure theories viously mentioned WWFE [13-23],the organizers of the exercise selected On the basis of the quantitative evaluation procedure used in the pre- Criterion,when the tensile and compressive strengths are assumed to be to note that equation (4.16)reduces to equation (4.14),the Tsai-Hill Mises Criteron for the yielding of isotropic materials.It is also interesting which causes equation (4.16)to take on the form of a generalized von More recently,Tsai and Hahn [37]have proposed the equation for the others,particularly in the fourth quadrant. imental data seems to be much better for the Tsai-Wu failure surface than an optimization procedure for FR In figure 4.3 the agreement with exper- failure surface for graphite/epoxy shown in figure 4.3 was based on such reader is referred to the articles by Wu [5,36]for details.The Tsai-Wu stresses.The optimization procedure is complicated,however,and the to account for the sensitivity of F1z to experimental scatter in the applied determine F2 accurately,the biaxial ration B=01/02 must be optimized different failure pairs o1,02.Wu [5,361 has suggested that in order to Hashin [31,F12 can have four different values,because there are four a priori reason that o1 must equal oz,however.Indeed,as pointed out by to the previously defined uniaxial and shear failure stresses.There is no Thus,in order to find F for this condition,we need to know P in addition and o=0 into equation(4.16),where p is the biaxial failure stress [34] can be obtained by substituting the biaxial stress conditions o1=02=p biaxial test involving both o1 and c2.For example,an expression for F In order to find theinteraction parameter,Fi2,it is necessary to use a where the numerical value of s)is assumed to be positive. From similar uniaxial and shear tests,it can be shown that where the numerical value of s)is assumed to be positive as in table 4.1. Principles of Composite Material Mechanics (420 (6.19 (418 · ply failure. stresses oy FIGURE 4.6 o,MPa -200 -100 兰 1800 and assumed linear elastic behavior up to initial ply failure.For Tsai et al.,[42,43]used the Tsai-Wu Criterion(i.e,equation 4.16) assumed.Additional features including progressive lamina failure were included for laminate analysis. ships,but nonlinear shear stress-shear strain behavior was up to initial failure in the normal stress-normal strain relation- dimensional version only).Linear elastic behavior was assumed Maximum Strain Criterion (i.e.,equations 4.5 are for the two- Bogetti et al.[40,41]employed a three-dimensional version of the failure prediction,additional features were included after first tic behavior was assumed up to initial failure.For laminate equations [4.21)to predict failure of a single lamina.Linear elas- Zinoviev et al.[38,39]used the Maximum Stress Criterion (i.e., the following five failure criteria: figure 4.7,the notations Zinoviev,Bogetti,Tsai,Puck,and Cuntze refer to and in-plane shear stresses txy in figure 4.7.In figure 4.6 and stresses ox and oy in figure 4.6 and under combined transverse normal results for unidirectional E-glass/epoxy materials under the biaxial normal surfaces for the five selected criteria are compared with experimental test and Technology,64(3-4),589-604.With permission.) epoxy laminae under combined normal stresses in directions parallel()and perpendicular ()to the fibers.(From Soden,P.D.,Kaddour,A.S.,and Hinton,M.J.2004.Composites Science Comparison of predicted and measured biaxial failure surface for unidirectional E-glass SR=32:1 -0 -200 3.7 -600 ---Bogetti Strength of a Continuous Fiber-Reinforced Lamina Ox MPa Experiments Cuntze g88

was added. FIGURE 4.7 should be selected for the purpose of lamina design. Txy MPa that produces the innermost portion of the failure surface in that quadrant such a way that,for a given quadrant of the failure surface,the theory mended that the combined theories of Tsai,Puck,and Cuntze be used in in several regions of both figure 4.6 and figure 4.7.Finally,it was recom- predictions of Zinoviev and Bogetti were observed to be unconservative sion-compression of figure 4.6,but fared better overall in figure 4.7.The data.The Puck predictions appeared to be unconservative in the ten- compression quadrant of figure 4.6 where there is a lack of experimental were believed to be potentially unconservative in the compression- ment with available experimental data [19].However,the Tsai predictions that the predictions of Tsai,Puck,and Cuntze gave the best overall agree- From figure 4.6 and figure 4.7,the organizers of the WWFE observed beyond the scope of this book. similar three-dimensional progressive failure theories,which are Puck and Schurmann [44,45]and Cuntze et al.[46,47]employed laminate failure prediction,a progressive failure analysis feature Technology,64(34),589-604.With permission.) fibers ()(From Soden,P.D.,Kaddour,A.S.,and Hinton,M.J.2004.Composites Sciencend laminae under combined in-plane shear stress (and normal stress perpendicular to the Comparison of predicted and measured failure surfaces for unidirectional E-glass/epoxy 罗 营 S L:8S'I- Tsai 100 Cuntze ,MTkx 电e Bogetti SR 1:2.】 Principles of Composite Material Mechanics P:1.62MPa. found as follows: theories EXAMPLE 4.3 be presented. (110312 (b)For the Tsai-Hill Criterion,equation(4.14)yields Thus,the transverse tensile failure governs,and failure occurs first at 0=6.0p=Sur=82.7 MPa;therefore,p=13.78 MPa 2=17.0p =s=27.6 MPa;therefore,p=1.62 MPa 1=20.5p=sL()=1103 MPa;therefore,p=53.8 MPa (a)For the Maximum Stress Criterion,the three possible values of p at failure are 2.3,1=20.5p,2=17.0p,and 12=6.0p (all in MPa).Note that both normal stresses are positive,so that the tensile strengths should be used in the failure Solution.The first step in the application of both theories is to determine the stresses along the principal material axes.From the results of example internal pressure p,which would cause failure of the vessel according to (a)the Maximum Stress Criterion and (b)the Tsai-Hill Criterion. The filament wound pressure vessel described in example 2.3 is fabricated from E-glass/epoxy having the lamina strengths listed in table 4.1.Determine the several micromechanical models for predicting composite strength will micromechanical behavior of fiber and matrix materials.In the next section, on the macromechanical behavior of the composite without regard for the systematic experimental verification of the various theories for a variety of stress conditions.Finally,the theories discussed in this section are based Although considerable progress has been made,there is still a need for the particular case of failure in laminated tubes under internal pressure loading,the cubic criterion is more accurate than the quadratic criterion. include cubic terms.Obviously,the evaluation of the strength parameters in such an equation is a formidable task.It was shown,however,that in failure modes should be modeled separately by a quadratic criterion. Tennyson et al.[48]have extended the tensor polynomial criterion to and its contributing stresses should be identified,and that each of these ites continues to be the subject of numerous publications.For example, Hashin [3,4]has suggested that for a given composite,each failure mode The development of improved multiaxial strength criteria for compos- Strength of a Continuous Fiber-Reinforced Lamina 器