
Problems with Lexical Semantics Polysemy:词通常有multitude of meanings和不同 用法。Vector Space Model不能区分同一个词的不 同含义,即ambiguity.. sime(d,q)<cos((d,q) Synonymy:不同的terms可能具有identical or a similar meaning.Vector Space Model.里不能表达词 之间的associations.. simrue(d,q)>cos((d,g) CCF-ADL at Zhengzhou University, June25-27,2010 12
Problems with Lexical Semantics • Polysemy: 词通常有multitude of meanings 和不同 用法。Vector Space Model不能区分同一个词的不 同含义,即ambiguity. • Synonymy: 不同的terms可能具有identical or a similar meaning. Vector Space Model里不能表达词 之间的associations. CCF-ADL at Zhengzhou University, June 25-27, 2010 12

Issues in the VSM ·terms.之间的独立性假设 -有些terms更可能在一起出现 ·同义词,相关词汇,拼写错误,etc. -根据上下文,termsi可能有不同的含义 ·term-document?矩阵维度很高 对每篇文档/每个词, 真的有那么多 重要的特征? CCF-ADL at Zhengzhou University, 13 June25-27,2010
Issues in the VSM • terms之间的独立性假设 – 有些terms更可能在一起出现 • 同义词,相关词汇,拼写错误,etc. – 根据上下文,terms可能有不同的含义 • term-document矩阵维度很高 对每篇文档/每个词, 真的有那么多 重要的特征? CCF-ADL at Zhengzhou University, June 25-27, 2010 13

Singular Value Decomposition DT Wid T rxr rxd txd t×r ■》 对term-document矩阵作奇异值分解Singular Value Decomposition ·r,矩阵的rank ■∑,singular values的对角阵(按降序排列) /D,T,具有正交的单位长度列向量(TT=l,DD'=) WWT的特征值 WW和WWT的特征向量 CCF-ADL at Zhengzhou University 14 June25-27,2010
Singular Value Decomposition ◼ 对term-document矩阵作奇异值分解 Singular Value Decomposition ◼ r, 矩阵的rank ◼ , singular values的对角阵(按降序排列) ◼ D, T, 具有正交的单位长度列向量(TT’=I, DD’=I) t d t r Wtd = T r r DT r d WWT的特征值 WTW和WWT的特征向量 CCF-ADL at Zhengzhou University, June 25-27, 2010 14
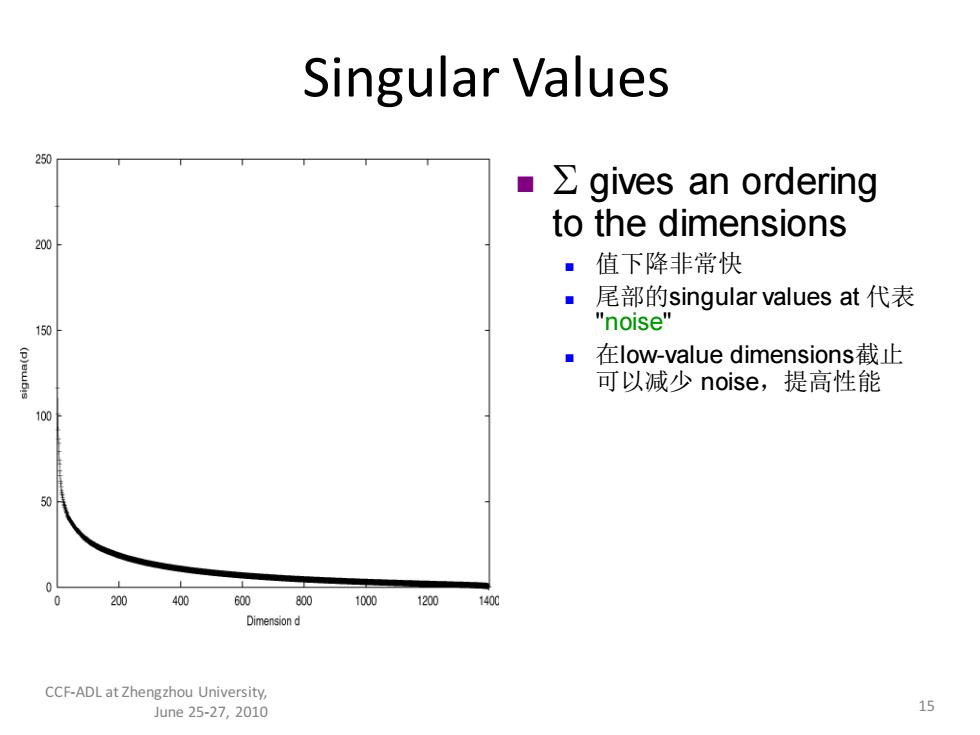
Singular Values ■ Σgives an ordering to the dimensions 200 ·值下降非常快 ■尾部的singular values at代表 "noise" ■在Iow-value dimensions截止 可以减少noise,提高性能 200 400 600 800 1000 1200 1400 Dimensiond CCF-ADL at Zhengzhou University, June25-27,2010 15
Singular Values ◼ gives an ordering to the dimensions ◼ 值下降非常快 ◼ 尾部的singular values at 代表 "noise" ◼ 在low-value dimensions截止 可以减少 noise,提高性能 15 CCF-ADL at Zhengzhou University, June 25-27, 2010
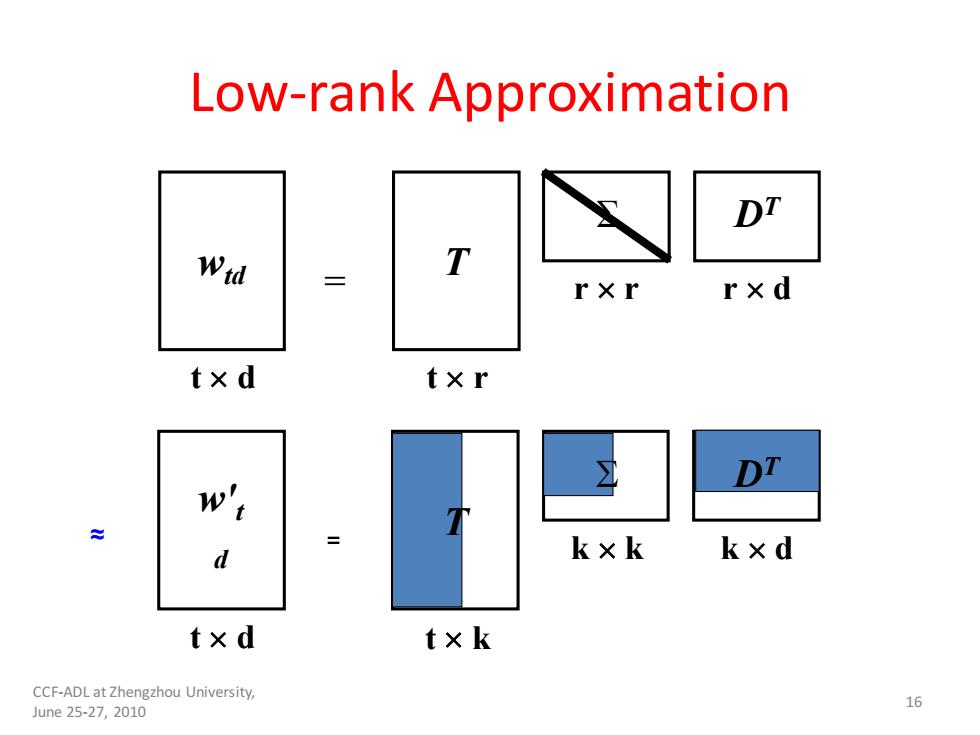
Low-rank Approximation DT Wid T rxd txd t×r DT d k×k k×d txd t×k CCF-ADL at Zhengzhou University, June25-27,2010 16
Low-rank Approximation t d t r wtd = T r r DT r d t d t k w't d = k k k d T DT ≈ CCF-ADL at Zhengzhou University, June 25-27, 2010 16