密钥协商 9 Diffie-Hellman密钥交换协议 端到端协议
密钥协商 Diffie-Hellman密钥交换协议 端到端协议

Diffie-.Hellman密钥交换协议 。Diffie-.Hellman密钥交换协议 ■它是由Diffie和Hellman在1976年提出的,它是一个典型的密钥协 商协议。通信双方利用该协议可以安全的建立一个共享密钥。 ·公开参数 ■设p是一个大素数,g∈Zn是一个本原元
Diffie-Hellman密钥交换协议 Diffie-Hellman密钥交换协议 它是由Diffie和Hellman在1976年提出的,它是一个典型的密钥协 商协议。通信双方利用该协议可以安全的建立一个共享密钥。 公开参数 设p是一个大素数,𝒈 ∈ 𝒁𝒑是一个本原元

Diffie-.Hellman密钥交换协议 ·协议过程 ■A随机选取a(2≤S-2),计算yg“modp,并将y4发送给B。 ■B随机选取b(2≤b-2),计算yB=gb mod p,并将yB发送给A。 ■A计算kyB“m0dp。 ■B计算ky b mod p. ■这样用户A和B就建立了一个共享密钥k=gab mod p,接下来他们就 可以使用对称密码体制以k为密钥进行保密通信了
Diffie-Hellman密钥交换协议 协议过程 A随机选取a(2≤a≤p-2),计算yA≡g a mod p,并将yA发送给B。 B随机选取b(2≤b≤p-2),计算yB≡g b mod p,并将yB发送给A。 A计算k≡yB a mod p。 B计算k≡yA b mod p。 这样用户A和B就建立了一个共享密钥k≡ g ab mod p,接下来他们就 可以使用对称密码体制以k为密钥进行保密通信了

Diffie-.Hellman密钥交换协议 ·例子 ■假设p=19,g=13,A和B分别选取随机数=3和b=5。A计算 y=133m0d19=12 ■并将y4发送给B。B计算 yB=135m0d19=14 ■并将yB发送给A。然后,A,B分别计算 k∈143mod19=8(A计算),k=125m0d19=8(B计算) ■这样A和B就获得了共享密钥=8
Diffie-Hellman密钥交换协议 例子 假设p=19, g=13, A和B分别选取随机数a=3和b=5。A计算 yA≡133 mod 19≡12 并将yA发送给B。B计算 yB≡135 mod 19≡14 并将yB发送给A。然后,A,B分别计算 k≡143 mod 19≡8(A计算),k≡125 mod 19≡8(B计算) 这样A和B就获得了共享密钥k=8
Diffie-Hellman密钥交换协议 。中间人攻击 a',b' A=ga mod p A'=ga'mod p A:a B:b B'=g5'mod p B-g5 mod p 敌手 K=gab'mod p K2=ga'b mod p ■敌手在A和B之间,截莸A和B传送的消息并替换成自己的消息。当 协议结束时,A与敌手建立了一个共享密钥K,B与敌手建立了一 个共享密钥K20 缺乏认证性
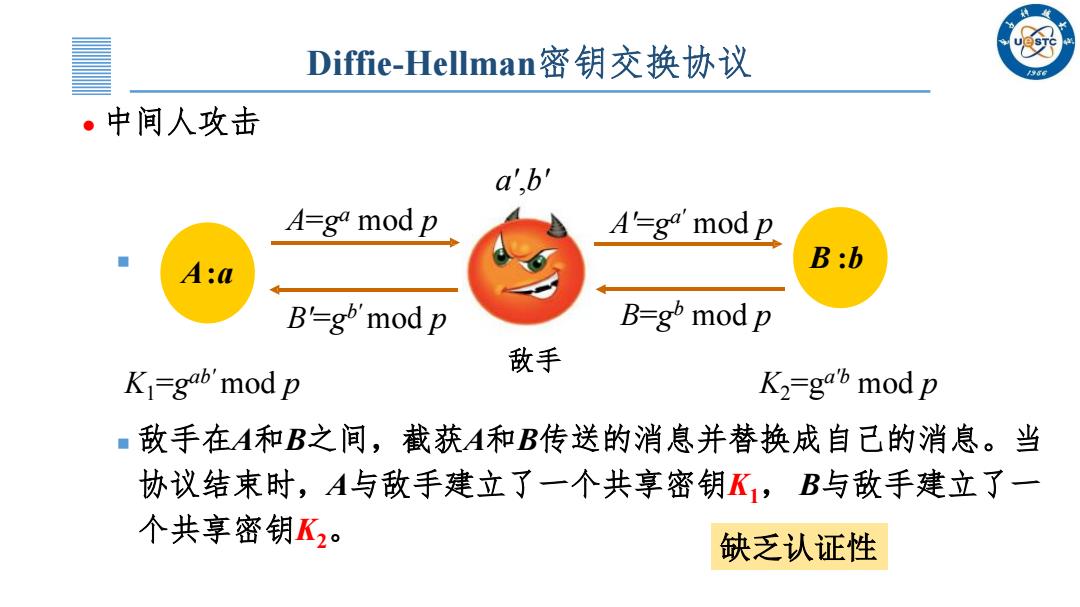
Diffie-Hellman密钥交换协议 中间人攻击 敌手在A和B之间,截获A和B传送的消息并替换成自己的消息。当 协议结束时,A与敌手建立了一个共享密钥K1, B与敌手建立了一 个共享密钥K2。 A=g a mod p B=g b mod p a',b' A'=g a' mod p B'=g b' mod p A:a B :b K1 =g ab' mod p K2 =g a'b mod p 敌手 缺乏认证性