
初期以来,每年都有许多国家级和省级鉴定的计量经济应用成果诞生。特别是在 一些省级以上的重点经济课题中,经济学硕士学位的论文中,如果没有模型技术 的应用,给人的印象总感分量不足。这些足以说明模型技术的应用在我国备受重 视。这里要强调说明的是,回归分析方法是模型技术中最基本的内容。 回归分析的理论和方法研究近200年来也得到不断发展,统计学中的许多重 要方法都与回归分析有着密切的联系。如时间序列分析、判别分析、主成分分 析、因子分析、典型相关分析等。这些都极大地丰富了统计学方法的宝库。 回归分析方法自身的完善和发展至今是统计学家研究的热点课题。例如自变 量的选择、稳健回归、回归诊断、投影寻踪、非参数回归模型等近年仍有大量研 究文献出现。 在回归模型中,当自变量代表时问、因变量不独立并且构成平稳序列时,这 种回归模型的研究就是统计学中的另一个重要分支 一时间序列分析。它提供了 一系列动态数据的处理方法,帮助人们科学地研究分析所获得的动态数据,从而 建立描述动态数据的统计模型,以达到预测、控制的目的。 在前面的回归模型(1.7)式中,因变量y和自变量x都是一维时,称它为一 元回归模型:当x是多维,y是一维时,则它为多元回归模型;若x是多维,y 也是多维的,则称它为多重回归模型。特别是当因变量观察矩阵Y的请行向量 假定是独立的,而列向量假定是相关的,就称为半相依回归方程系统。 对于满足基本假设的回归模型,它的理论已经成熟,但对于违背基本假设的 回归模型的参数估计问题近些年仍有较多研究。 在实际问题的研究应用中,人们发现经典的最小二乘估计的结果并不总是令 人满意的,统计学家们从多方面进行努力试图克服经典方法的不足。例如,为了 克服设计矩阵的病态性,提出了以岭估计为代表的多种有偏估计。Stein于1955 年证明了当维数p大于2时,正态均值向量最小二乘估计的不可容性,即能够 找到另一个估计在某种意义上一致优于最小二乘估计,从此之后人们提出了许多 新的估计,其中主要有岭估计、压缩估计、主成分估计、Stein估计,以及特征 根估计、偏最小二乘法。这些估计的共同点是有偏的,即它们的均值并不等于待 估参数,于是人们把这些估计称为有偏估计。当设计矩阵X呈病态时,这些估 计都改进了最小二乘估计。 为了解决自变量个数较多的大型回归模型的自变量的选择问题,人们提出了 许多关于回归自变量选择的准测和算法;为了克服最小二乘估计对异常值的敏感 性,人们提出了各种稳健回归;为了研究模型假设条件的合理性及样本数据对统 计推断影响的大小,产生了回归诊断;为了研究回归模型(1.7)中未知参数非线 16 PDF created with pdfFactory Pro trial version www.pdffactory.com
PDF created with pdfFactory Pro trial version www.pdffactory.com

性的问题,提出了许多非线性回归,这其中有利用数学规划理论提出的非线性回 归参数估计方法、样条回归方法、微分几何方法等:为了分析和处理高维数据。 特别是高维非正态数据,产生了投影寻踪回归、切片回归等。参见参考文献 [41]、[45]。 近年来,新的研究方法不断出现,如非参数统计、自助法、刀切法、经验贝 叶斯估计等方法都对回归分析起着渗透和促进作用。 由此看来,回归模型技术随着它本身的不断完善和发展以及应用领域的不断 扩大,必将在统计学中占有更重要的位置,也必将为人类社会的发展起着它独到 的作用。 思考与练习 1.变量间统川关系和函数关系的区别是什么? 2.回归分析与相关分析的区别与联系是什么? 3.回归模型中随机误差项ε的意义是什么? 4.线性回归模型的基本假设是什么? 5.回归变量的设置理论根据是什么?在回归变量设置时应注意哪些问题? 6.收集、整理数据包括哪些内容? 7.构造回归理论模型的基本根据是什么? 8.为什么要对回归模型进行检验? 9.回归模型有哪几个方面的应用? 10,为什么强调运用回归分析研究经济问题要定性分析和定量分析相结合? PDF created with pdfFactory Pro trial version www.pdffactory.com
PDF created with pdfFactory Pro trial version www.pdffactory.com

第2章 线常南年球带金艺据南品的 一元线性回归 一元线性回归是描述两个变量之间统计关系的最简单的回归模型。一元线性 回归虽然简单,但通过一元线性回归模型的建立过程,我们可以了解回归分析方 法的基本统计思想以及它在实际问题研究中的应用原理。本章将详细讨论一元线 性回归的建模思想、最小二乘估计及其性质、回归方程的有关检验、预测和控制 的理论及应用。 2.1一元线性回归模型 一、一元线性回归横型的实际背景 在实际问题的研究中,经常需要研究某一现象与影响它的某一最主要因素的 关系。如影响粮食产量的因素非常多,但在众多因素中,施肥量是一个最重要的 因素,我们往往器要研究施肥量这一因素与粮食产量之间的关系;在消费问题的 研究中,影响消费的因素很多,但我们可以只研究国民收入与消费额之间的关 系,因为国民收入是影响消费的最主要因索;保险公司在研究火灾损失的规律 时,把火灾发生地与最近的消防站的距离作为一个最主要因素,研究火灾损失与 18 PDF created with pdfFactory Pro trial version ww.pdffactory.com
PDF created with pdfFactory Pro trial version www.pdffactory.com
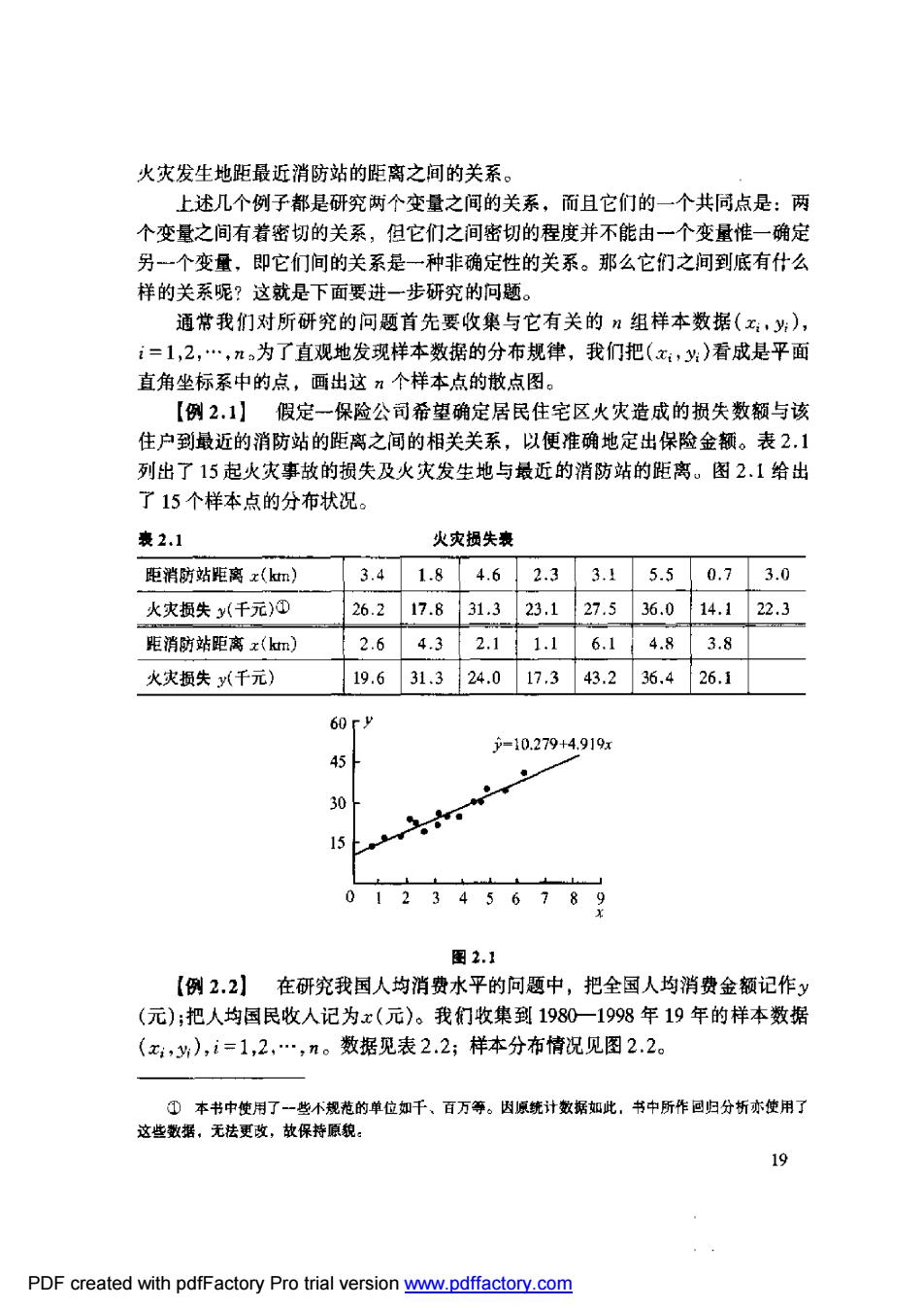
火灾发生地距最近消防站的距离之间的关系。 上述几个例子都是研究两个变量之间的关系,而且它们的一个共同点是:两 个变量之间有着密切的关系,但它们之间密切的程度并不能由一个变量惟一确定 另一个变量,即它们间的关系是一种非确定性的关系。那么它们之间到底有什么 样的关系呢?这就是下面要进一步研究的问题。 通常我们对所研究的问题首先要收巢与它有关的n组样本数据(x,y), i=1,2,…,为了直观地发现样本数据的分布规律,我们把(,”)看成是平面 直角坐标系中的点,画出这”个样本点的散点图。 【例2.1】假定一保险公司希望确定居民住宅区火灾造成的损失数额与该 住户到最近的消防站的距离之间的相关关系,以便准确地定出保险金额。表2.1 列出了15起火灾事故的损失及火灾发生地与最近的消防站的距离。图2.1给出 了15个样本点的分布状况。 表2.1 火灾损失表 距消防站距离x(km) 3.41.84.62.33.15.50.73.0 火灾损失y(千元)① 26.217.831.323.127.536.014.123 距消防站距离x(km) 2.64.32.11.16.14.83.8 火灾损失y千元) 19.631.324.017.343.236.426.1 60 户=10.279+4.919x 45 w. 0123456789 图2.1 【例2,2】在研究我国人均消费水平的问题中,把全国人均消费金额记作y (元):把人均国民收人记为x(元)。我们收集到19801998年19年的样本数据 (x,y),i=1,2,…,n。数据见表2.2;样本分布情况见图2.2。 ①本书中使用了一些规花的单位如千、百万等。因原统计数据如此,书中所作回归分析亦使用了 这些数据,无法更改,故保持原貌。 19 PDF created with pdfFactory Pro trial version www.pdffactory.com
PDF created with pdfFactory Pro trial version www.pdffactory.com

表2.2 人均国民收入表 年份人均国民收人(元人均消费金额(元)年份人均国民收人(元)人均消费金额(元) 460 234.7 1990 1634 797.08 259.20 199 1879 890.66 1982 525 280.5 1992 2287 1063.39 198 580 305.97 1993 2939 1323.22 1984 692 347,15 1994 3923 1736.32 1985 B53 433.5 1995 4854 2224.59 1986 956 481,36 19g6 5576 2627.06 1987 1104 545.40 10g7 6053 2819.36 1988 1355 687.51 1998 6392 2958.18 1989 1512 756.27 4000r八元) 3000 2000 00( 0 2000 40006000x800 图2.2 从图2.1和图2.2我们看到,上面两个例子的样本数据点(x,y)大致都分 别落在一条直线附近。这说明变量x与y之间具有明显的线性关系。从图上还 看到,这些样本点又不都在一条直线上,这表明变量x与y的关系并没有确切 到给定x就可以惟一确定y的程度。事实上,对y产生影响的因素还有许多,如 人均消费金额不仅受人均国民收人的影响,还与上年的消费水平、银行利率、商 品价格指数等有关,这些对y的取值都有随机影响。把每个样本点与直线的偏 差就可看做是其他随机因素的影响。 二、一元钱性回归模型的数学形式 像上面两个例子都是只考虑两个变量间的关系,描述上述x与y间线性关 系的数学结构式可看作是上章中回归模型(1.7)式的特例,即当(1.7)式中p=1】 时的情况。亦即 y=0+月1x+c (2.1) (2.1)式将实际问题中变量y与x之间的关系用两个部分描述。一部分是由 20 PDF created with pdfFactory Pro trial version www.pdffactory.com
PDF created with pdfFactory Pro trial version www.pdffactory.com