
的问题中,其变量x与y之间的关系并不总是具有这种“回归”的含义,但借 用这种名词把研究变量x与y间统计关系的量化方法称为“回归”分析也算是 对高尔顿这个伟大的统计学家的纪念。 1.3回归分析的主要内容及其一般模型 一、回归分析研究的主要内容 回归分析研究的主要对象是客观事物变量间的统计关系,它是建立在对客观 事物进行大量试验和观察的基础上,用来寻找隐藏在那些看上去是不确定的现象 中的统计规律性的统计方法。回归分析方法是通过建立统计模型研究变量间相互 关系的密切程度、结构状态、模型预测的一种有效的工具。 回归分析方法在生产实践中的广泛应用是它发展和完善的根本动力。如果从 19世纪初(1809年)高斯(Gauss)提出最小二乘法算起,回归分析的历史已有190 多年。从经典的回归分析方法到近代的回归分析方法,它们所研究的内容已非常 丰高。如果按研究的方法来划分,回归分析研究的范围大致如下: ·元线性回归 线性回归子多元线性回归 多个因变量与多个自变量的回归 [讨论如何从数据推断回归模型基本假设的合理性 回归诊断 当基本假设不成立时如何对数据进行修正 判定回归方程拟合的效果 选择回归函数的形式 回归变量的选择 」自变量选择的准则 回归分析 逐步回归分析方法 岭回 参数估计方法的改进主成分回归 偏最小二乘法 一元非线性回归 非线性回归分段回归 多元非线性回归 含有定性变量的回归/自变量含定性变量的情况 !因变量是定性变量的情况 6 PDF created with pdfFactory Pro trial version www.pdffactory.com
PDF created with pdfFactory Pro trial version www.pdffactory.com

二、回归模型的一般形式 如果变量x1,x2,…,x,与随机变量y之间存在着相关关系,通常就意味 着每当x1,x2,…,xp取定值后,y便有相应的概率分布与之对应。随机变量 y与相关变量x,x,,xp之间的概率模型为 v=fx1,x2.…,xp)+e (1.6) 其中,随机变量y称为被解释变量(因变量);x1,x2,…,x称为解释变量 (自变量)。在计量经济学中,也称因变量为内生变量,自变量为外生变量: f代x1,x2,…,cp)为一般变量x1,x2,…,xb的确定性关系,e为随机误差。正 是因为随机误差项€的引人,才将变量之间的关系描述为一个随机方程,使得我 们可以借助随机数学方法研究y与x1,x2,…,x的关系。由于客观经济现象 是错综复杂的,一种经济现象很雅用有限个因素来准确说明,随机误差项可以概 括表示由于人们的认识以及其他客魂原因的局限而没有考虑的种种偶然因索。随 机误差项主要包括下列因素的影响: 1.由于人们认识的局限或时间、费用、数据质量等制约未引入回归模型但 又对回归被解释变量y有影响的因素: 2.样本数据的采集过程中变量观测值的观测误差的影响: 3.理论模型设定误差的影响: 4.其他随机因素的影啊。 模型(1.6)式清楚地表达了变量x1,x2,…,xe与随机变量y的相关关系, 它由两部分组成:一部分是确定性函数关系,由回归函数f代x1,x2,…,x)给出: 另一部分是随机误差项ε。由此可见模型(1.6)式准确地表达了相关关系那种既 有联系又不确定的特点。 当概率模型(1.6)式中回归函数为线性函数时,即有 y=+1x1t2x2t…+月p+e (1.7) 其中,风,月1,品2,,丹。为未知参数,常称它们为回归系数。线性回归模型 的“线性”是针对未知参数A(i=0,1,2,…,p)而言的。对于回归解释变量的线 性是非本质的,因为解释变量是非线性时,常可以通过变量的替换把它转化成线 性的。 如果{x1,x2,…,xp;y,),i=1,2,…,n是(1.7)式中变量(x1,x2,…,xp y)的一组观测值,则线性回归模型可表示为 y=%+B1x1+2.x21…'rp+e,i=1,2,…,n (1.8 为了估计模型参数的需要,古典线性回归模型通常应满足以下几个基本假设: PDF created with pdfFactory Pro trial version www.pdffactory.com
PDF created with pdfFactory Pro trial version www.pdffactory.com

1.解释变量t1,x2,…,t是非随机变量,观测值x1,x2,…,x是 常数。 2.等方差及不相关的假定条件为 E(e,)=0,i=1,2,…,n .=j1,2.,n) 10,≠j 这个条件称为高斯-马尔柯夫(Gauss-Markov)条件,简称G-M条件。在此条 件下,便可以得到关于回归系数的最小二乘估计及误差项方差。2估计的一些重 要性质,如回归系数的最小二乘估计是回归系数的最小方差线性无偏估计等。 3.正态分布的假定条件为 eN(0,c2),i=1,2,…,n 1,e2,…,9*相互独立 在此条件下便可得到关于回归系数的最小二乘估计及。2估计的进一步的结果, 如它们分别是回归系数及。的最小方差无偏估计等,并且可以作回归的显著性 检验及区间估计。 4.通常为了便于数学上的处理,还要求n>p,即样本容量的个数要多于解 释变量的个数。在整个回归分析中,线性回归的统计模型最为重要。一方面是因 为线性回归的应用最广泛;另一方面是只有在回归模型为线性的假定下,才能得到 比较深人和一般的结果;再就是有许多非线性的回归模型可以通过适当的转化变 为线性回归问题进行处理。因此,线性回归模型的理论和应用是本书研究的重点。 对线性回归模型我们通常要研究的问题有: 1.如何根据样本(x1,x2…,py),i=1,2,…,n求出风,月1,2…,月,及 方差。2的估计: 2.对回归方程及回归系数的种种假设进行检验; 3.如何根据回归方程进行预测和控制,以及如何进行实际问题的结构分析。 1.4建立实际问题回归模型的过程 在实际问题回归分析模型的建立和分析中有几个重要的阶段,为了给读者 个整体印象,我们以经济模型的建立为例,先用逻辑框图表示回归模型的建模过 程。见图1.3。 下面我们按逻辑框图顺序叙述每个阶段要做的工作以及应注意的问题 PDF created with pdfFactory Pro trial version www.pdffactory.com
PDF created with pdfFactory Pro trial version www.pdffactory.com
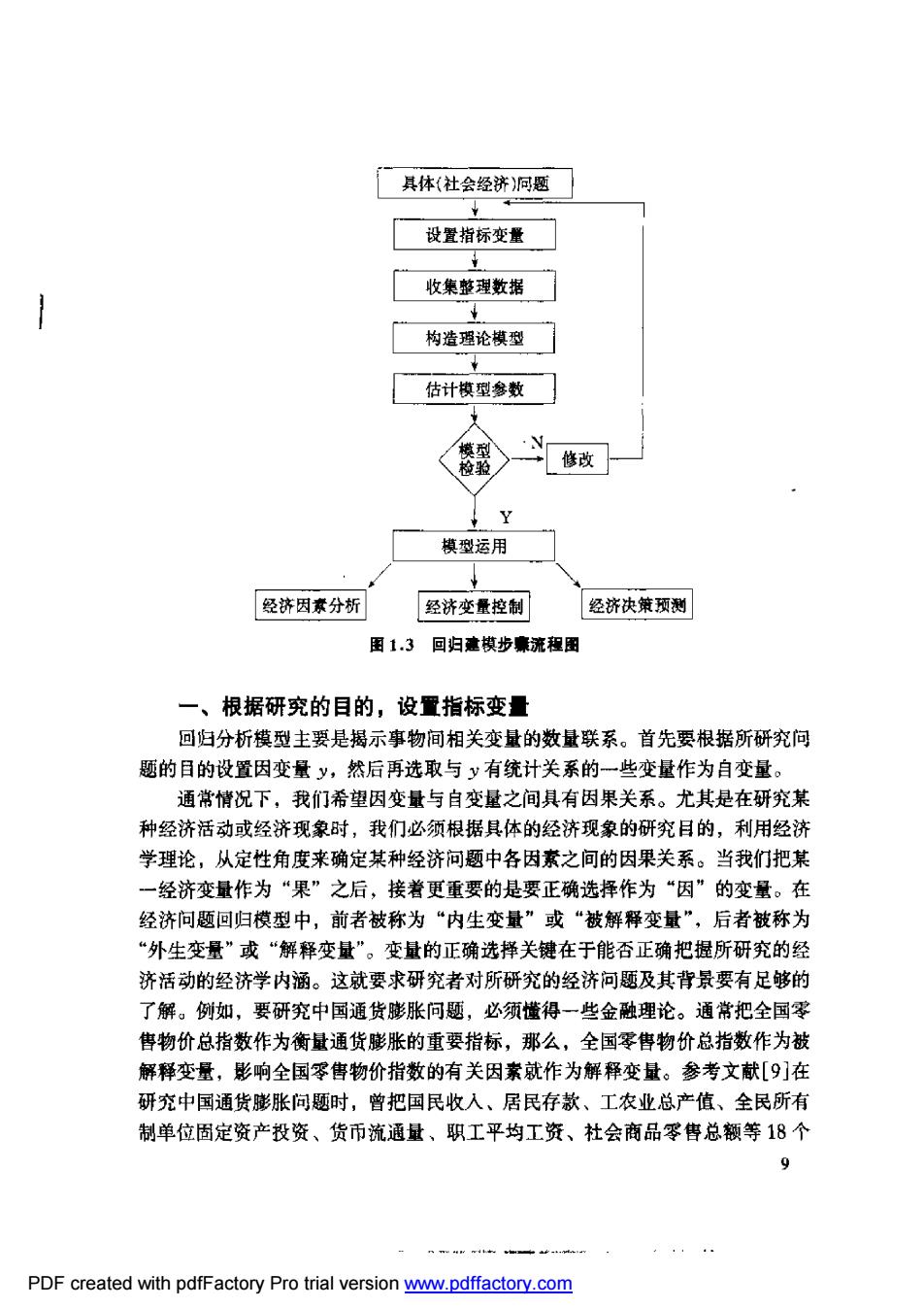
「具体(社会经济同题 设置指标变量 收集整理数据 1 构造理论模型 估计模型参数 模型运用 经济因素分析 经济变量控制 经济决策两测 图1.3回归意模步廉流租图 一、根据研究的目的,设置指标变量 回归分析模型主要是揭示事物间相关变量的数量联系。首先要根据所研究问 题的目的设置因变量y,然后再选取与y有统计关系的一些变量作为自变量: 通常情况下,我们希望因变量与自变量之间具有因果关系。尤其是在研究某 种经济活动或经济现象时,我们必须根据具体的经济现象的研究目的,利用经济 学理论,从定性角度来确定某种经济问题中各因素之间的因果关系。当我们把某 一经济变量作为“果”之后,接着更重要的是要正确选择作为“因”的变量。在 经济问题回归模型中,前者被称为“内生变量”或“被解释变量”,后者被称为 “外生变量”或“解释变量”。变量的正确选择关键在于能否正确把提所研究的经 济活动的经济学内涵。这就要求研究者对所研究的经济河恶及其背景要有足够的 了解。例如,要研究中国通货膨胀问题,必须懂得一些金融理论。通常把全国零 售物价总指数作为衡量通货膨胀的重要指标,那么,全国零售物价总指数作为被 解释变量,影响全国零售物价指数的有关因素就作为解释变量。参考文献[9]在 研究中国通货膨胀问题时,曾把国民收入、居民存款、工农业总产值、全民所有 制单位固定资产投资、货币流通量、职工平均工资、杜会商品零售总额等18个 PDF created with pdfFactory Pro trial version www.pdffactory.com
PDF created with pdfFactory Pro trial version www.pdffactory.com

指标确定为解释变量。参考文献[37]在研究中国储蓄被动机理中,曾把各项银行 存款作为被解释变量,把货币发行量、全国零售物价指数、股票价格指数、银行 利率、国债利率、居民收入等16个指标确定为解释变量。 对一个具体的经济问题,当研究目的确定之后,被解释变量容易确定,被解 释变量-般直接表达、刻画研究的目的。就像参考文献[9]、[37]中根据研究的问 题,直接将全国零售物价总指数和银行存款分别作为通货膨胀问题和储蓄问题的 被解释变量。而对被解释变量有影响的解释变量的确定就不太容易。一是由于我 们的认识有局限,可能并不知道对被解释变量有重要影响的因素。二是为了模型 参数估计的有效性,设置的解释变量之间应该是不相关的。我们很难确定哪些变 量是相关的,哪些不是相关的、因为在经济问题中很难找到影响同一结果的一些 因素它们之间是独立的。这就看我们如何在多个变量中确定儿个重要的、且不相 关的变量。三是我们从经济关系角度考虑非常重要的变量应该引进,但是在实际 中并没有这样的统计数据。这一点,在我国建立经济模型时经常会遇到。这时 可以考虑用相近的变量代替,或者由其他几个指标复合成·个新的指标。 在选择变量时要注意与一些专门领城的专家合作。研究金融模型,就要与 些金融专家和具体业务人员合作;研究粮食生产问题,就要与衣业部门的一些专 家合作。这样做可以帮助我们确定模型变量。 另外,不要认为一个回归模型所涉及到的解释变量越多越好。一个经济祺 型,如果把一些主要变量漏掉肯定会影响模型的应用效果,但如果细枝末节-起 进人模型也未必就好。当引人的变量太多时,可能选择了·些与问题无关的变 量,还可能由于一些变量的相关性很强,它们所反映的信息有较严重的重叠,这 就出现共线性问题。当变量太多时,计算工作量太大,计算误差积累也大,估计 出的模型参数精度自然不高。 总之,回归变量的确定是一个非常重要的问题,是建立回归模型最基本的工 作。这个工作一般一次并不能完全确定,通常要经过反复试算,最终找出最适合 的一些变量。这在今天计算机的帮助下,已变得不太困难了。 二、收集、整理统计数据 回归模型的建立是基于回归变量的样本统计数据。当确定好回归模型的变量 之后,就要对这些变量收集、整理统计数据。数据的收集是建立经济问题回归模 型的重要一环,是一项基础性工作,样本数据的质量如何,对回归模型的水平有 至关重要的影响。 常用的样本数据分为时间序列数据和横截面数据。 10 PDF created with pdfFactory Pro trial version www.pdffactory.com
PDF created with pdfFactory Pro trial version www.pdffactory.com