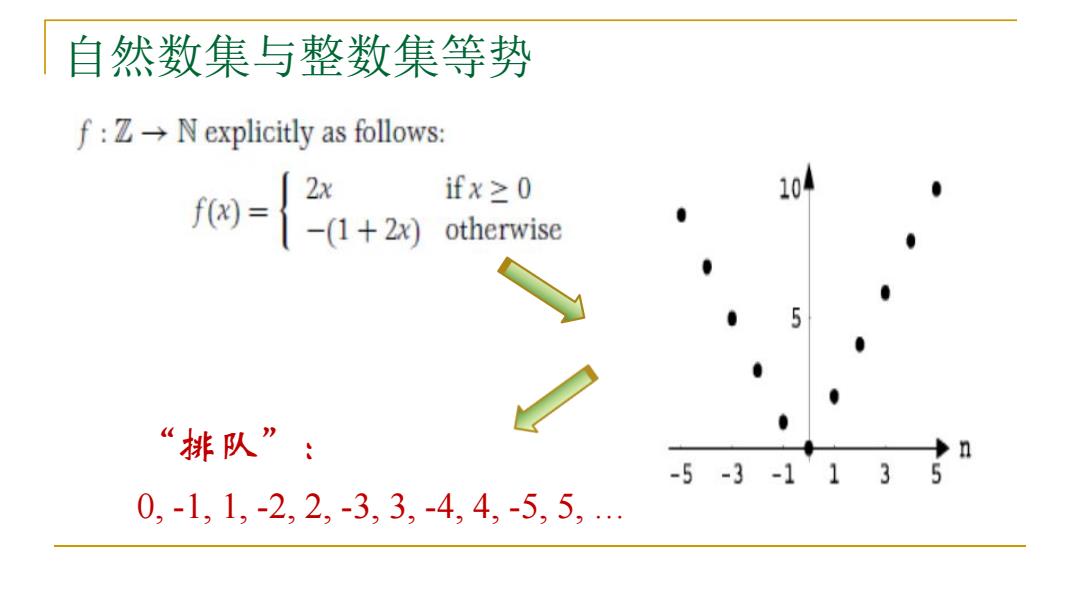
自然数集与整数集等势 f:ZN explicitly as follows: 0-+2对 ifx≥0 104 otherwise “排队”: n -5-3-1135 0,-1,1,-2,2,-3,3,-4,4,-5,5,…
自然数集与整数集等势 “排队” : 0, -1, 1, -2, 2, -3, 3, -4, 4, -5, 5, …

问题5: 6.a-3,-2,-1,0,12,3,9不 能算排好队了,为什么?

关于双射的证明(1) f:ZN explicitly as follows: 注意: 2x f=1 ifx≥0 不能遗漏了case3! -(1+2x)otherwise Proof that f is one-to-one. Letm,n∈Z and suppose that f(m)≠f(n). Case 1.Suppose that m0 and n z0.Then f(m)=2m and f(n)=2n.Thus 2ni =2n,and therefore m=n. Case 2.Suppose that m<0 and n 0.Then f(m)=-2m-1 and f(n)=-2n-1.Thus,-2m-1 =-2n-1,and therefore m =n. Case 3.S Suppose that one of the two,say m,is nonnegative,and the other is negative.Then f(m)=2m and f(n)=-2n-1. Thus 2m =-2n-1.But this means that an even number, 2m,is equal to an odd number,-2n-1,which is impossible. Therefore,if f(m)=f(n),only case 1 and case 2 can occur.In either of these cases,we have shown that m =n.Thus f is one-to- one. ■
关于双射的证明 (1) 注意: 不能遗漏了case 3!

关于双射的证明(2) f:ZN explicitly as follows: f-{2+2 2x ifx≥0 otherwise Proof that f maps Z onto N. Letk∈N.If k is even,then k=2 m for some m∈Z with m≥O. Thus,m eZ and f(m)=2m k.If k is odd,then k+1 is even. Hence m=(k+1)/(-2)∈Z.Since k≥1,we have m<0.Thus, f(m)=-2m-1 =-2((k +1)/(-2))-1 k.We conclude that for allk∈N,there exists m∈Z such that f(m)=k.Sincef:Z→Nis a well-defined function,f maps Z onto N. ■
关于双射的证明 (2)

无穷不仅仅是“很多很多 Not necessary It is possible to define comparisons 伽利略悖论: amongst infinite sets in a meaningful way! 整体与局部“一样大”】 23 4 5 67 8 Galileo Galilei 1625 36 49 64.. The ideas of less,equal,and greater apply to (what we would now call)finite sets,but not to infinite sets https://en.wikipedia.org/wiki/Galileo%27s paradox
无穷不仅仅是“很多很多” 伽利略悖论: 整体与局部“ 一样大”! https://en.wikipedia.org/wiki/Galileo%27s_paradox Galileo Galilei The ideas of less, equal, and greater apply to (what we would now call) finite sets, but not to infinite sets! Not necessary! It is possible to define comparisons amongst infinite sets in a meaningful way!