
计算机问题求解一论题2-12 堆与堆排序 2018年05月14日
计算机问题求解 – 论题2-12 - 堆与堆排序 2018年05月14日

堆性质 如果我们要定义堆 的ADT,在其数据 部分,我们应该给 出什么约束? ·树T满足偏序树性质当且仅当树中任一结点的键值不小于 (或不大于)其子结点(如果有)的键值。 树T满足几乎完全二叉性质 口最底一层可能不满,但必须从左到右填充
堆性质 ◼ 树T 满足偏序树性质 当且仅当 树中任一结点的键值不小于 (或不大于)其子结点(如果有)的键值。 ◼ 树T满足几乎完全二叉性质 ❑ 最底一层可能不满,但必须从左到右填充 如果我们要定义堆 的ADT,在其数据 部分,我们应该给 出什么约束?

间题1: 堆与我们上次讨论的队列与 栈最突出的差别是什么? 其特征与对象的内容相关, 一定是源于具体应用
其特征与对象的内容相关, 一定是源于具体应用
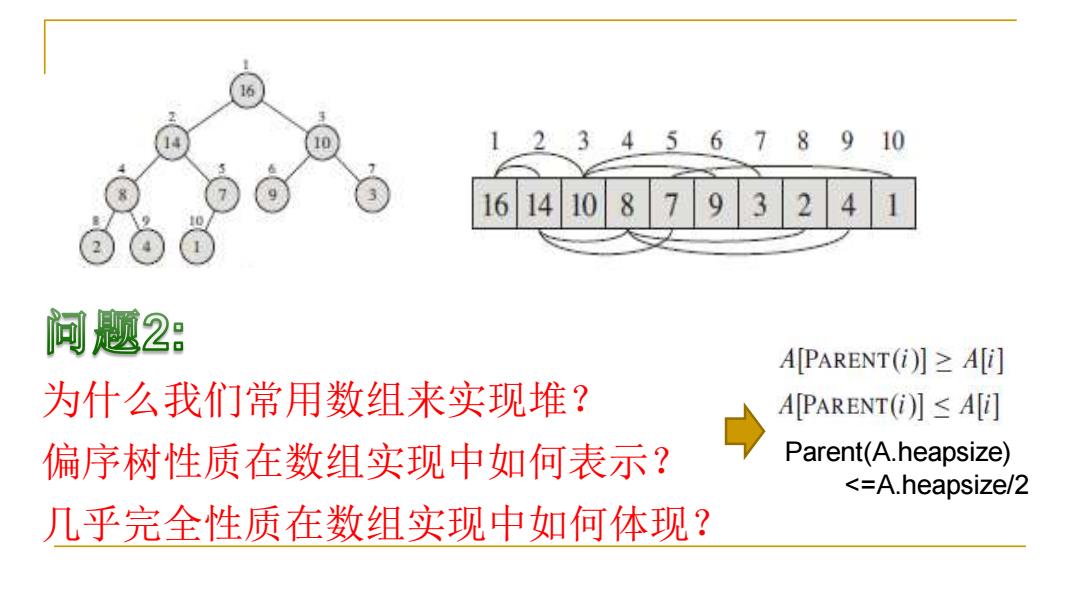
6 12345678910 1614108793241 问题2: A[PARENT(i)】≥A[] 为什么我们常用数组来实现堆? A[PARENT(i)】≤A[叮 偏序树性质在数组实现中如何表示? Parent(A.heapsize) <=A.heapsize/2 几乎完全性质在数组实现中如何体现?
为什么我们常用数组来实现堆? 偏序树性质在数组实现中如何表示? 几乎完全性质在数组实现中如何体现? Parent(A.heapsize) <=A.heapsize/2
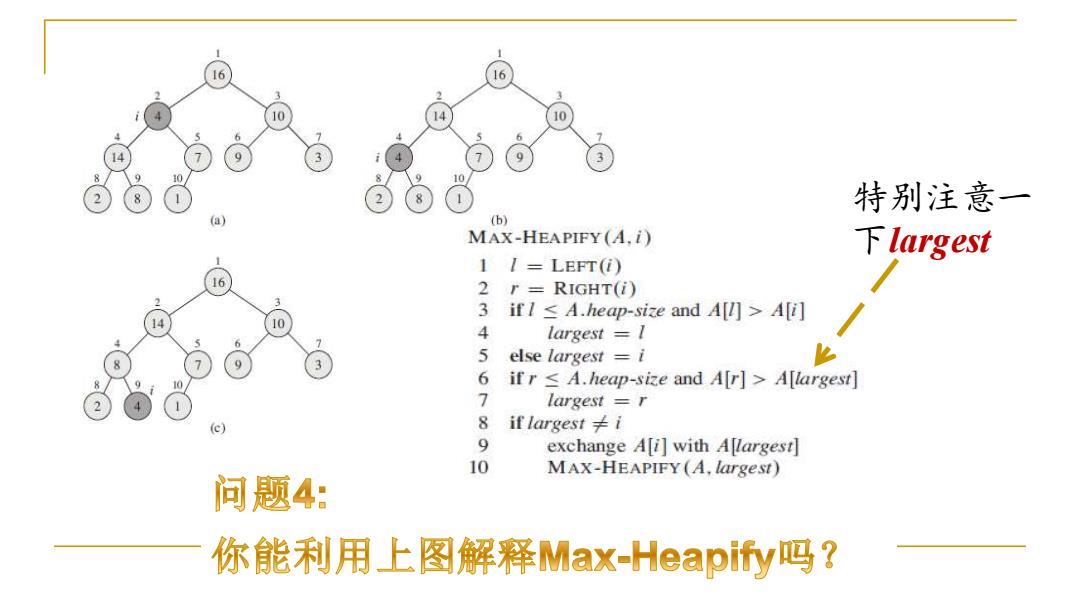
16 10 特别注意 (b) MAX-HEAPIFY(A.i) 下largest 1 /LEFT(i) 2 r=RIGHT(i) 3 if I A.heap-size and A[l]>A[i] 4 largest =I 5 else largest =i 6 if r A.heap-size and A[r]>A[largest] 7 largest =r 8 if largest≠i 9 exchange A[i]with A[largest] 10 MAX-HEAPIFY(A,largest) 问题4: 你能利用上图解释Max-Heapify!吗?
特别注意一 下largest