
第4章频率域滤波 139 这个表达式就是我们寻找的离散傅里叶变换D给定一个由f)的M个样本组成的集合{},式(4.44) 得出一个与输入样本集合离散傅里叶变换相对应的M个复数离散值的样本集合{F}。反之,给定 {F},我们可以用傅里叶反变换(DFT)复原样本集{f}: 五-空em.a=a2M- (4.45) 不难证明(见习题4.8),把式(4.45)的/n代入式(4.44)可得出F=Fn。类似地,把式(4.44)的F 代入式(4.45)得到f,=f。这意味着式(4.44)和式(4.45)组成了一个离散傅里叶变换对。此外,这 些恒等式指出,对于任何其值有限的样本集合,正、反傅里叶变换都是存在的。注意。这两个表达式 不明确地依赖于取样间隔△T,也不依赖于式(4.43)中的频率间隔。因此。离散傅里叶变换对适用于 任何均匀取样的有限离散样本集。 在前面的阐述中,我们使用m和来表示离散变量,因为对于推导来说历来都是这样做的。然 而,特别是在二维情况下,使用x和y表示图像坐标变量并使用“和v表示频率变量更为直观,在这 里,这些变量可理解为整数。这样,式(4.44)和式(4.45)就变为 ∑fx0e21MM=0.12,…,M- (4.46) f()-M eFwe2w.x=0.l2…,M-l1 (4.47) 为简便起见,我们在上式中使用函数表示代替了下标2。显然,F()=F且fx)=。从这一点出 发,我们用式(4.46)和式(4.47)表示一维DFT对。某些作者通过在式(4.46)中包含1/M项来代替我 们在式(4.47)中所示的方法。这不会影响两个公式形成一个傅里叶变换对的证明。 可以证明(见习题4.9),傅里叶正变换和反变换都是无限周期的,其周期为M,即 F(u)=F(u+kM) (4.4-8) f(x)=f(x+kM) (4.49 考虑到对连续函数取样的结果不 其中,k是整数 是的离函数是周期函 式(4.2-20)中的卷积的离散等价表示是 数正式方法是,记 DT中的取样结果反DT的 之fmh-ml (4.410) 果/对于DT对的存在来说必明 是周期的。 x=0,1.2.·,M-1。因为在前面的公式中的函数是周期的.所以它门的参积也是周期的。式(4.410)给H 了周期卷积的一个周期。由于这一原因,在这个公式中,其内在处理通常称为循环卷积,并且直接 导致DT和它的反变换的周期性。这与我们在342节中研究的卷积形成了对比,在该卷积中,位移 周期内额率从最低到最高的样本。这是为符号表示 两侧的样本因为后者要求使用负号。463节将时论对变换数序的过 2使用:表示连续空间变量及使用表示连续频率变量时。我们一直非常小心。从现在起。我将使用x和“来分别表示一维离4网 245
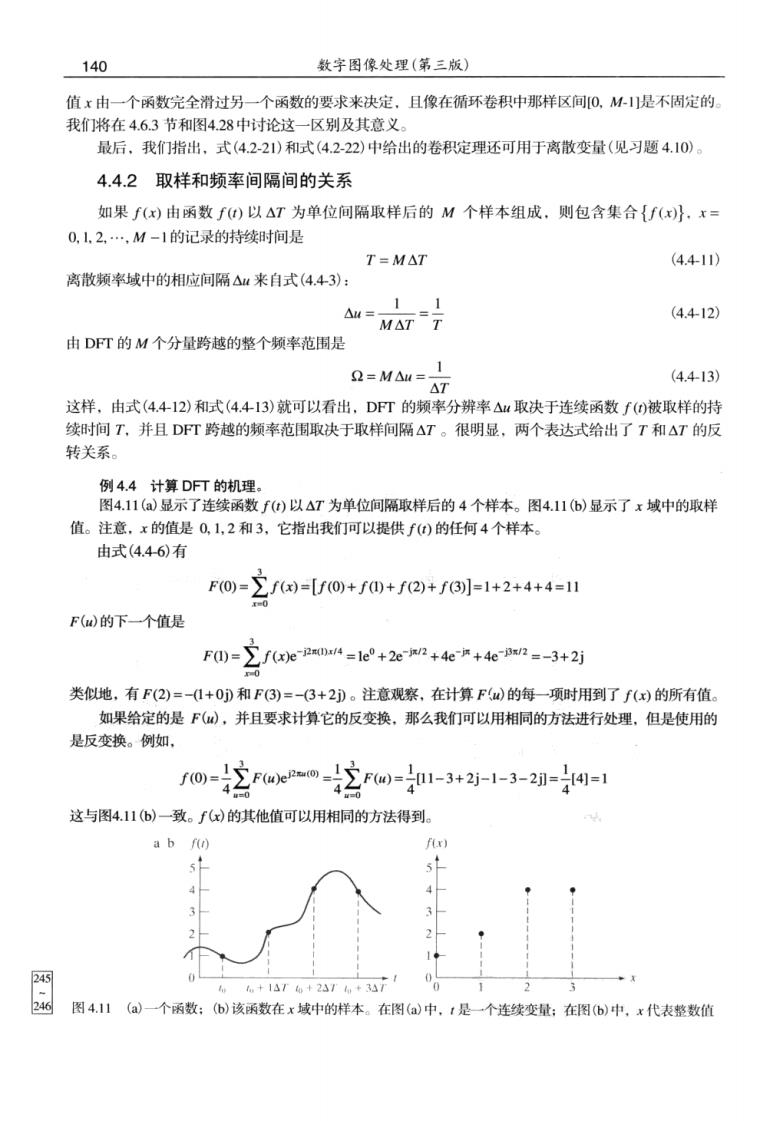
140 数字图像处理(第三版) 值x由一个函数完全滑过另一个函数的要求来决定.且像在循环卷积中那样区间0.M1]是不周定的 我们将在4.6.3节和图4.28中讨论这一区别及其意义 最后,我们指出、式(4.2-21)和式(4.2-22)中给出的卷积定理还可用于离散变量(见习题4.10)。 4.4.2取样和频率间隔间的关系 如果f(x)由函数f)以△T为单位间隔取样后的M个样本组成,则包含集合{f(x)}.x= 0.12,,M-1的记录的持续时间是 T=M△7 (4.4-11) 离散频率域中的相应间隔△u来自式(4.43): △= (4.4-12 由DFT的M个分量跨越的整个频率范围是 =Mau= (4.4-13) 这样,由式(4.412)和式(4.413)就可以看出,DFT的频率分辨率△4取决于连续函数f()被取样的持 续时间T,并且DT跨越的频率范围取决于取样间隔△T。很明显,两个表达式给出了T和△T的反 转关系。 例4.4计填D丁的机理 图4.11(a显示了连续函数f0)以△T为单位间隔取样后的4个样本。图4.11(6)显示了x域中的取样 值。注意,x的值是0,1,2和3,它指出我们可以提供f)的任何4个样本。 由式(446)有 F0-立f=/0+f0+f2)+f6例-1+2+4+4=Ⅱ F()的下一个值是 F0)=∑∫xe24=1e°+2ew2+4e+4ewn=-3+2j 0 类似地,有F(2)=-1+0)和F(3)=-(3+2D。注意观察,在计算F4)的每一项时用到了f(x)的所有值 如果给定的是F(),并且要求计算它的反变换,那么我们可以用相同的方法进行处理,但是使用的 是反变换。例如。 fo=2Fwe-2F)=-3+2j-1-3-2-- 这与图4.11(6)一致。∫x)的其他值可以用相同的方法得到。 a b fur) f(x 6+131+27+71 图A心一选做在技中的样本调中,是一个球变在锅中代表型

第4章频率域滤波 141 4.5两个变量的函数的扩展 在这一节,我们将把4.2节到4.4节介绍的概念扩展到两个变量。 4.5.1二维冲激及其取样特性 两个连续变量t和z的冲激6(,)被定义为如式(4.2-8)所示的形式: 0-合0 (4.5-1a) ∫∫广6,tk=l (4.5-1b) 如在一维情况那样,二维冲激在积分下呈现了取样特性: ∫∫f0.6e.zdk=f0.0 (4.5-2) 或者,更一般地,对位于坐标(。)处的冲激,有 ∫fu.60-62-o灿d=fho) (4.5-3) 如以前那样,我们看到,取样特性在冲激所在的位置产生函数∫么,的值 对于离散变量x和y,二维离散冲激定义为 6(x-y-) 6(xy)= 1,x=y=0 (45-4 0.其他 其取样特性为 r.nsc.n-1. (4.5-5) 式中,fx,是离散变量x和y的函数。对于一个 图4.12二维单位离散冲激。变量x和y是离散的.且 位于坐标(,%)外的冲激(见图4.12),其取样特 6的值在除坐标(x,y)外的任何位置都为0 性为 ∑∑fky8x-y-w)=f6o (45-6) 如以前那样,离散冲激的取样特性在该冲激所在的位置产生离散函数∫化,y的值。 4.5.2二维连续傅里叶变换对 令∫化,)是两个连续变量!和z的连续函数。则其一维连续傅里叶变换对由以下两个表达式给出: Fa,w=∫∫fu,zear*ed女 (4.5-7) f.)=F(u.v)eRdu dy 4.5-8

142 数字图像处理(第三版) 其中,4和v是频率变量。当涉及图像时,1和z解释为连续空间变量。就像一维情祝那样,变量山 和v的域定义了连续频率城。 例4.5得到一个简单函数的二维傅里叶变换。 图4.13显示了一个模仿例4.1中一维情况的二维函数。按照类似于例4.1中使用的过程给出结果 (4T)(Z) 其幅度(谱)由下面的表达式给出: r 图4.13)显示了关于原点的谱的一部分。正如一维的情祝那样,在谱中零的位置与T和Z的值成反 比。这样,T和Z越大,则谐将变得更“收缩”,反之亦然。 a b f.z) 12Z2: 图4.3()一个二维函数:(6)该二维函数的谱的一部分(未按比例画出) 该块沿:轴越长。则沿μ轴的谱更“紧凑”。请与图4.4比较 4.5.3二维取样和二维取样定理 类似于一维情况中的方式,二维取样可用取样函数(二维冲激串)建模: w小-2-ar-a (4.5-9) 其中,△T和△Z是连续函数f化,)沿1轴和z轴的样本 54Ay(,2) 间的间隔。式(4.5-9)描述了沿着两个轴无限扩展的周期 神中激的集合(见图4.14)。如图4.5中说明的一维情况那样 用s应化,z)乘f化,)可得到取样后的函数 如果由区间-4x,4m】和区间-V,V】建立 的矩形之外的傅里叶变换是零,则函数f心,)称为带限 函数;即 F(u,)=0.川≥H.且≥v (4.5-10) 图4.14二维冲激串 二维取样定理表明,如果取样间隔满足 且 AT<2Ho (4.5-11)

第4章频率域滤波 143 (4.5-12) 或者关于取样率的表达, >24 (4.5-13) 和 (4.5-14 △☑ 则连续带限函数f化,可以由其一组样本无误地恢复。另一种叙述方法是:我们说。如果一个二维带 限连续函数在山和v两个方向上由以大于该承数最高顺率两倍的取样率取样获得的样本表示,则没右 信息丢失。 图415显示了图4.6(6)和()的一维等效图示。个理想的一维盒状浅波器有图413(a)说明的形 式。图4.15()中的虚线部分说明了滤波器的位置,以便达到分离从其样本重建带限函数必要的变换 的单个周期,正如4.33节那样。由4.34节,我们知道,如果函数欠取样,则周期将会重叠,并且如 图4.15(6)所示,分离出单个周期是不可能的。在这样的条件下,将产生混淆。 ab 图4.15(a)过取样和6)欠取样带限函数的二维傅里叶变换 4.5.4图像中的混淆 在这一节,我们把混涌的概念扩展到图像,并讨论一些与图像取样和重取样有关的问题。 从一维混淆展开 正如在一维情况下那样,如果只在两个坐标方向上无限扩展,二维连续变量:和z的连续函数通 常可以被带限。限制一个函数时间的非常动作将引起在频率域无限扩展的有害的频率分量,正如4.3.4 节所解释的那样。因为我们不可能对一个函数无限地取样,所以,正像在取样后的一维函数中所存在 的那样,在数字图像中混淆总是存在的。在图像中,存在两种主要的混涌现象:空间混淆和阳时间混涌。 如4.3.4节讨论的那样,空间混淆是由欠取样造成的。时间混淆与图像序列中图像间的时间间隔有关。 时间混淆最常见的例子之一是“车轮”效应,即在序列图像(如电影)中具有轮辐的车轮出现倒转的现 象。这是由于序列中的顿率低于轮子转动的速度引起的。 在这一章,我们重点关注空间混淆。图像中空间混涌的主要表现形式是人为引入的缺陷,如线 24网 状特征中的锯齿、伪高光及原图像中不存在的模式的出现。下面的例子说明了图像中的混涌。 251