
第3章灰度变换与空间滤波 它的与众不同之处在于,是透过光线看阴影还是透过阴影看亮度」 一大卫·林赛 引言 术语空间域指图像平面本身,这类图像处理方法直接以图像中的像素操作为基础。这是相对于 变换域中的图像处理而言的,正如2.6.7节所介绍的和第4章将要详细讨论的那样,变换域的图像处 理首先把一幅图像变换到变换域,在变换域中进行处理,然后通过反变换把处理结果返回到空间域。 空间域处理主要分为灰度变换和空间滤波两类。正像本章您将了解到的那样,灰度变换在图像的单个 像素上操作,主要以对比度和阂值处理为目的。空间滤波涉及改善性能的操作,如通过图像中每一个 像素的邻域处理来锐化图像。接下来几节我们将讨论一些经典的灰度变换和空间滤波技术。我们还将 讨论模糊技术的某些细节,以便允许我们在灰度变换和空间滤波算法的公式化表示中并人不太精确的 以知识为基础的信息。 3.1背景知识 3.1.1灰度变换和空间滤波基础 本节讨论的所有图像处理技术都是在空间域进行的。由2.4.2节的讨论,我们知道空间域就是简 单的包含图像像素的平面。如2.6.7节定义的那样,与(第4章的主题)频率域相反,空间域技术直 接在图像像素上操作,例如,对于频率域来说,其操作在图像的傅里叶变换上执行,而不针对图像本 身。正如您将在阅读全书的过程中了解到的那样,某些图像处理任务在空间域中执行更容易或更有意 义,而另一些任务则更适合使用其他方法。通常,空间域技术在计算上更有效,且在执行上需要较少 的处理资源。 本章讨论的空间域处理可由下式表示: g(x,y=TLf(x,y川 (3.1-1) 其中f(x,y)是输入图像,g(x,y)是处理后的图像,T是在点(x,y)的 有时也使用其他形状的邻碱。如 邻域上定义的关于∫的一种算子。算子可应用于单幅图像(本章中我 圆的数 近似。 矩形邻域是到 们的主要关注点)或图像集合,例如,如2.6.3节中讨论的那样,为降 前为止最好的邻域,因为它们在 算机上实现起来更为容易

第3章灰度变换与空间滤波 63 低噪声而对图像序列执行逐像素的求和操作。图3.1显示了式(3.1)在单幅图像上的基本实现。所示 的点(化,)是图像中的一个任意位置,包含该点的小区域是点(xy)的邻,如2.65节解释的那样。 典型地,邻城是中心在(x,y)的矩形.其尺寸比图像小得多 图3.1中给出的处理由以下几北组成:邻域原点从一 原点 个像素向另一个像素移动。对邻域中的像素应用算子T】 并在该位置产生恰出。这样,对于任意指定的位置(x,v) c.y 输出图像g在这些坐标处的值就等于对∫中以(x,)为原 (化)的3×3邻城 点的邻域应用算子T的结果。例如,假设该邻城是大小为 3×3的正方形.算子T定义为“十算该邻域的平均灰度” 图像 考虑图像中的任意位置,譬如000,150)。假设该邻域的 空间域 原点位于其中心处,则在该位置的结果g100,150)是计算 100,150)和它的8个邻点的和,再除以9(即由邻域包 图3】空间域图像中关于点(化,y)的一个 围的像素灰度的平均值)。然后,邻域的原点移动到下 3×3邻域邻域在车图像中从个像个素 个位置,并重复前面的过程,产生下一个输出图像g的值 到另一个像素移动来生成一幅输出图像 典型地,该处理从输入图像的左上角开始以水平扫描的方式逐像素地处理,每次一行。当该邻域的 原点位于图像的边界上时,部分邻域将位于图像的外部。此时,不是在用T做指定的计算时忽略外侧 邻点,就是用0或其他指定的灰度值填充图像的边缘。被填充边界的厚度取决于邻域的大小。在3.4, 节中,我们将再回到这一问题 就像我们在3.4节中羊细计论的那样。则网则描术的时程称为空间滤波,其中,邻域与陌定义的操 作一起称为空间滤波器(也称为空间模核模板或窗口)。在邻域中执行的操作类型决定了滤波处 理的特性。 最小邻域的大小为1×1。在这种情祝下,8仅取决于点(x)处的∫值,而式(3.1)中的T则成 为一个形如下式的灰度(也称为灰度级或映射)变换函数: s=T(r) (3.1-2 其中,为表达方便,令r和s分别表示变量,即g和f在任意点(x,y)处的灰度。例如,如果T)有 如图3.2()所示的形式,对∫中每一个像素施以变换产生相应的8的像素的效果将比原始图像有更高 的对比度,即低于k的灰度级更暗,而高于k的灰度级更亮。这种技术有时称为对比度拉伸(见3.2.4 节),在该技术中,低于k的r值被变换函数压缩在一个较窄的范围s内。接近黑色:而高于k的,值 则与此相反。很明显,灰度值经映射得到了相应的值。。在如图3.26)所示的极限情况下,T) 产生了一幅两级(二饱图像。这种形式的映射称为闲值处理函数。有些相当简单但功能强大的处理方 法,可以使用灰度变换函数用公式加以表达。在这一章中,我们主要使用灰度变换函数来进行图像增 强。在第0章中,我们将使用灰度变换函数来进行图像分割。其结果仅取决于一个点处的灰度的方 法有时称为,点处理技术,与此相反,本节早些时候讨论的方法则称为邻域处理技术。 3.1.2关于本章中的例子 虽然灰度变换和空间滤波覆盖了相当宽的应用范围,但本章中的多数例子是图像增强应用。增 强处理是对图像进行加工,使其结果对于特定的应用比原始图像更合适的一种处理。“特定” 一词在 这里很重要,它一开始就确定增强技术是面向问题的。例如,对于增强X射线图像非常有用的方法, 可能并不是增强由电磁波谱中远红外波段拍摄的图像的最好方法。图像增强没有通用的“理论”。当2可 为视觉解释而处理幅图像时。观察者将是判定一种特定方法好与坏的最终栽判员。在处理机器感知园

64 数字图像处理(第三版) 时,一种给定的技术很易于量化。例如,在自动字符识别系统中,最合适的增强方法就是可得到最好 识别名的方法,这里不考虑一种方法较另一种方法的计算量的要求。 ab s=T() s■7() T()- T(n) 暗人亮 图32灰度变换函数:(对比度拉伸函数:6)闲值处理函数 然而,不管应用或使用过的方法,图像增强是视觉上最具吸引力的图像处理领域之一。理所当 然地,图像处理的初学者通常会寻找重要的且理解起来相对简单的增强应用。因此,使用图像增强的 例子来说明本章中论述的空间处理方法,不仅可以节省本书中处理图像增强的额外的章节,而且更重 要的是对初学者介绍空间域处理技术的细节的更有效方法。正如您将要看到的那样,随着本书的进程 本章叙述的基本内容可用于比图像增强宽得多的范围。 3.2 一些基本的灰度变换函数 灰度变换是所有图像处理技术中最简单的技术。?和5分别代表处理前后的像素值。如前一节指 出的那样,这些值与s=)表达式的形式有关,其中T是把像素值r映射到像素值s的一种变换。由 于我们处理的是数字量,所以变换函数的值通常存储在一个一维阵列中,且从到s的映射是通过查 找表实现的。对于8比特环境,包含T的值的一个查找表将有256条记录。 作为关于灰度变换的介绍,考虑图33,该图显示了图像增强常用的三类基本函数:线性函数(反 转和恒等变换)、对数函数(对数和反对数变换)和幂律函数(n次幂和n次根变换)。恒等函数是最一 般的情况,其输出灰度等于输人灰度的变换,在图3.3中包括它仅仅为了完整性考虑。 3.2.1图像反转 使用图3.3中所示的反转变换,可得到灰度级范围为0,L-的一幅图像的反转图像,该反转图 像由下式给出: s=L-1-r (3.2.1 使用这种方式反转一辐图像的灰度级,可得到等效的照片底片。这种类型的处理特别适用于增强嵌入 在一幅图像的暗区域中的白色或灰色细节,特别是当黑色面积在尺寸上占主导地位时。图3.4显示了 一个例子。原图像是一幅数字乳房X射线照片,其中显示有一小块病变。尽管事实上两幅图在视觉 内容上都一样,但应注意,在这种特殊情况下,分析乳房组织时使用反转图像会容易得多 3.2.2对数变换 图 图3.3中的对数变换的通用形式为 s=clog(+r) (3.2-2)
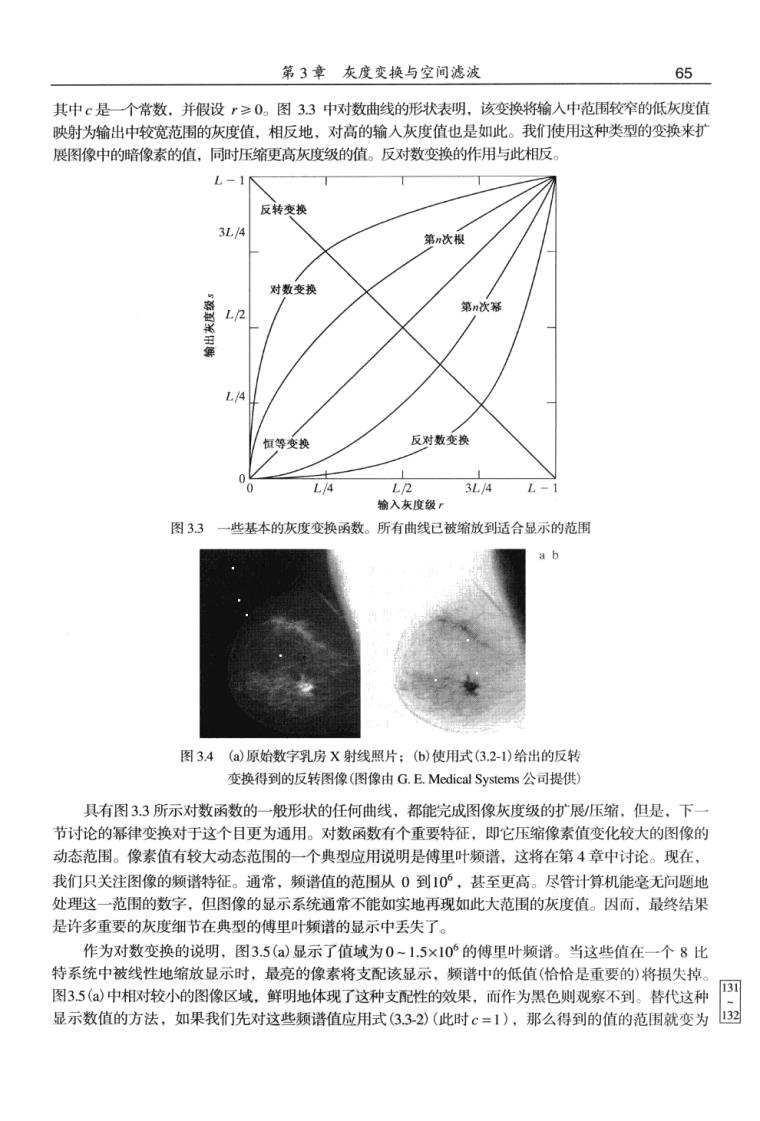
第3章灰度变换与空问滤波 65 其中是一个常数.并假设r≥0。图33中对数曲线的形状表明.该变换将输入中范围较窄的低灰度值 映射为输出中较宽范围的灰度值,相反地,对高的输入灰度值也是如此。我们使用这种类型的变换来剁 展图像中的暗像素的值,同时压缩更高灰度级的值。反对数变换的作用与此相版。 L-10 反转变换 3L/4 第n次根 对数变换 第次 反对数变换 3L4 L- 输入灰度级r 图33一些基本的灰度变换函数。所有曲线已被缩放到适合品示的范围 a b 图34(a原始数字乳房X射线照片:(6)使用式(3.2-1)给出的反转 变换得到的反转图像(图像由G.E.Medical Systems公司提供) 具有图3.3所示对数函数的一般形状的任何曲线,都能完成图像灰度级的扩展压缩,但是,下一 节讨论的幂律变换对于这个目更为通用。对数函数有个承要特征,即它压缩像素值变化较大的图像的 动态范围。像素值有较大动态范围的一个典型应用说明是傅里叶频谱,这将在第4章中讨论。现在。 我们只关注图像的矩礼特征。通常.额滤情的节围从0到10其至申高。尽管十值机能宴无问颗地 处理这一范围的数字,但图像的显示系统通常不能如实地再现如此大范围的灰度值。因而,最终结 是许多重要的灰度细节在典型的傅里叶频谱的显示中丢失了。 作为对数变换的说明,图3.5(a)显示了值域为0-1.5×10°的傅里叶频谱。当这些值在一个8比 特系统中被线性地缩放显示时,最亮的像素将支配该显示,频谱中的低值(恰恰是重要的)将损失掉。 图35(a)中相对较小的图像区域,鲜明地体现了这种支配性的效果,而作为黑色则观察不到。替代这种 显示数值的方法,如果我们先对这些频谱值应用式(3.32》(此时=1),那么得到的值的范围就变为 图
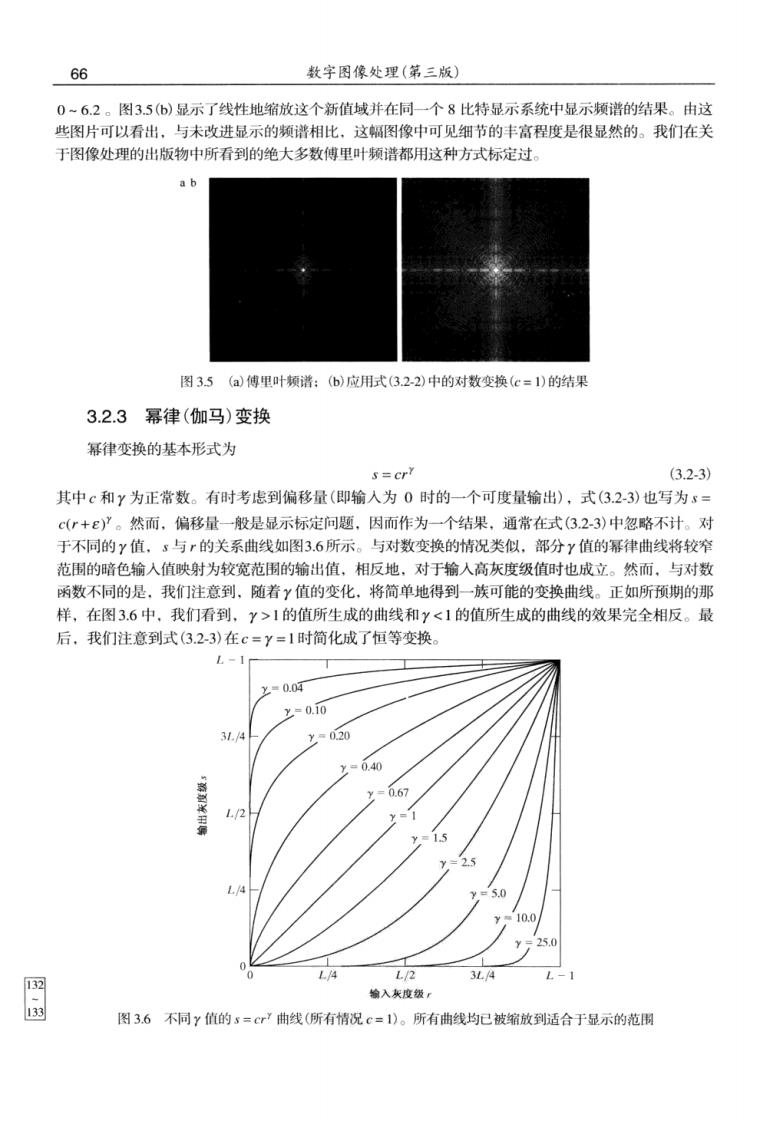
66 数字图像处理(第三版) 0一6.2。图35(6)显示了线性地缩放这个新值域并在同一个8比特显示系统中显示频谱的结果。由这 些图片可以看出,与未改进显示的频谱相比.这幅图像中可见细节的丰富程度是很显然的。我们在关 于图像处理的出版物中所看到的绝大多数傅里叶颜谱都用这种方式标定过。 ab 图35(a)傅里叶频谱:(b)应用式(3.2-2)中的对数变换(c=1)的结果 3.2.3幂律(加马)变换 幂律变换的基本形式为 s=cr (323) 其中c和y为正常数。有时考虑到偏移量(即输入为0时的一个可度量输出),式(3.23)也写为s c(r+ε了。然而,偏移量一般是显示标定问题,因而作为一个结果.通常在式3.2-3)中忽略不计。对 于不同的y值,s与r的关系曲线如图3.6所示 与对数变换的情祝类似,部分Y值的幂律曲线将较 范围的暗色输入值映射为较宽范围的输出值,相反地,对于输人高灰度级值时也成立。然而,与对数 函数不同的是,我们注意到.随着Y值的变化,将简单地得到一族可能的变换曲线。正如所预期的那 样,在图3.6中,我们看到,Y>1的值所生成的曲线和y<1的值所生成的曲线的效果完全相反。最 后,我们注意到式(3.23)在c=Y=1时简化成了恒等变换。 L-1 y=0.10 31. 040 667 15 2 入灰度级 图36不同y值的s='曲线(所有情况c=)。所有曲线均已被缩放到适合于显示的范围