(7) 为等压摩尔热容:其大小等于1ml的理想气体在等压过程中每单位温升中向外界吸收的 热量。 (2)Cpm和Cvm的关系 M dv 将(5)代入(7)可得 mPd7,由理想气体状态方程可得,在等压过程 ,代入上式可得 Cpm Crm+R (8) 引入g表示定压热容与定容热容的比值,即 1-Cvn 三、等温过程 1.在pV图上是一条双曲线。 0 图6-3等温线 实际例子:水锅中上升的气泡。 2.特点 (1)内能不变,原因是什么? (2)系统对外所作的功等于和热量系统从外界吸收的热量: Q=W, 具体计算:系统从状态A(pl,V1,T)等温变化到状态B(p2、V2、T)过程中,系统对 外所作的功为
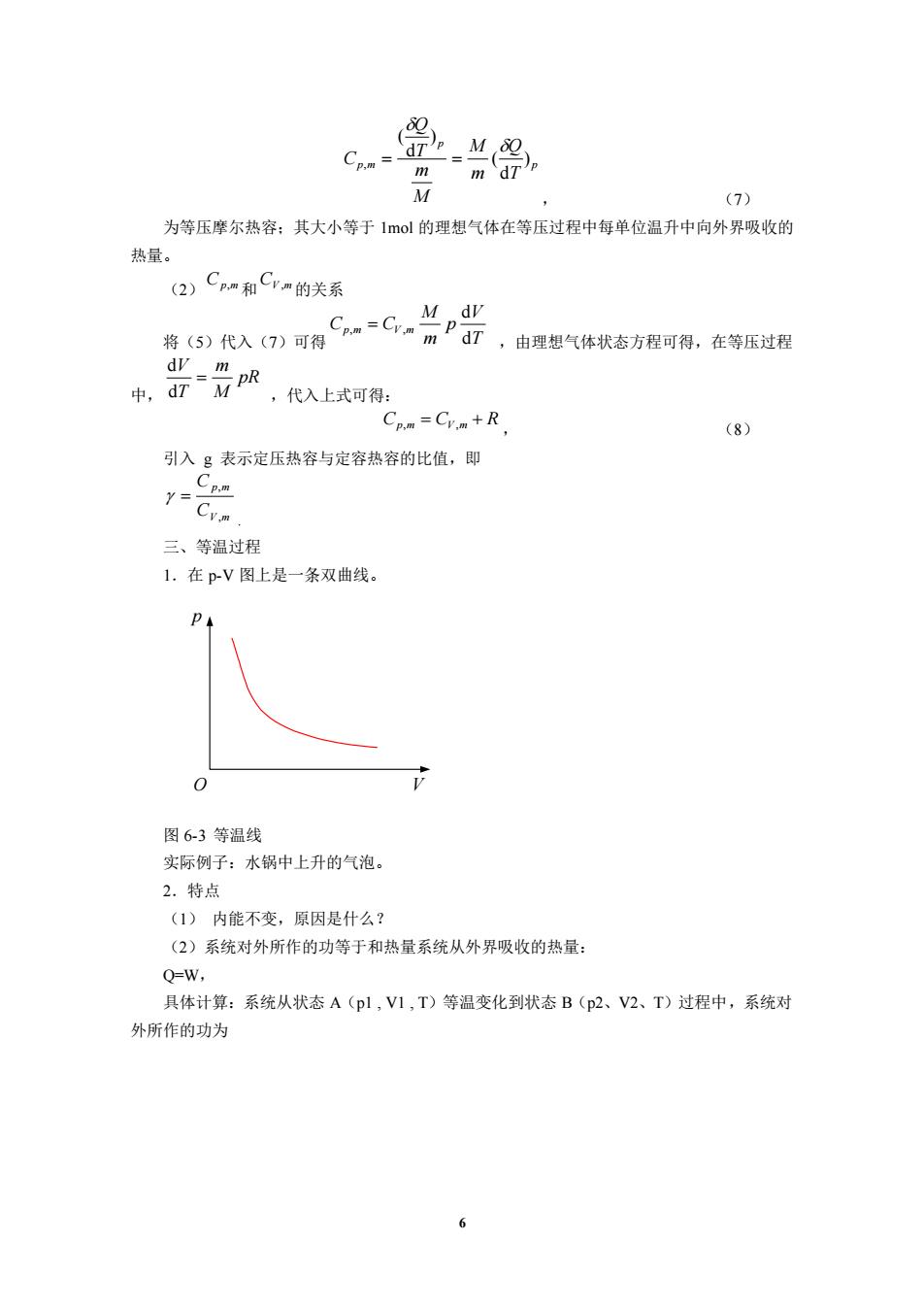
6 p p p m T Q m M M m T Q C ) d ( ) d ( , = = , (7) 为等压摩尔热容;其大小等于 1mol 的理想气体在等压过程中每单位温升中向外界吸收的 热量。 (2) Cp,m 和 CV ,m 的关系 将(5)代入(7)可得 T V p m M Cp m CV m d d , = , ,由理想气体状态方程可得,在等压过程 中, pR M m T V = d d ,代入上式可得: Cp,m = CV ,m + R , (8) 引入 g 表示定压热容与定容热容的比值,即 V m p m C C , , = . 三、等温过程 1.在 p-V 图上是一条双曲线。 p O V 图 6-3 等温线 实际例子:水锅中上升的气泡。 2.特点 (1) 内能不变,原因是什么? (2)系统对外所作的功等于和热量系统从外界吸收的热量: Q=W, 具体计算:系统从状态 A(p1 , V1 , T)等温变化到状态 B(p2、V2、T)过程中,系统对 外所作的功为
pd Ra M 1) PV=PV,. M (2) 四、绝热过程(dQ-0) 1.由第一定律推导功的表达式绝热过程:Q=0,△4=W,用物理语言表述:绝热过程 中系统内能的增加等于外界对系统所作的功。 2.内能的变化为 AE=MCav(T-T) 3) 将理想气体状态方程代入可得: AE-C(pV:-pY) (4) 注意上述讨论适合于静态和非静态绝热过程 3.准静态绝热过程 (1)准静态绝热过程的过程方程泊松公式 0 图64绝热过程 考虑一个无限小的准静态过程,气体对外界所作的元功为聊=PP,内能增量为 E-Cd ,注意到绝热过程0=0,因此由热力学第一定律得 C dT+-0 (5) 而理想气作态方我P一灯 ,可得 r+pr-是随7 (6)
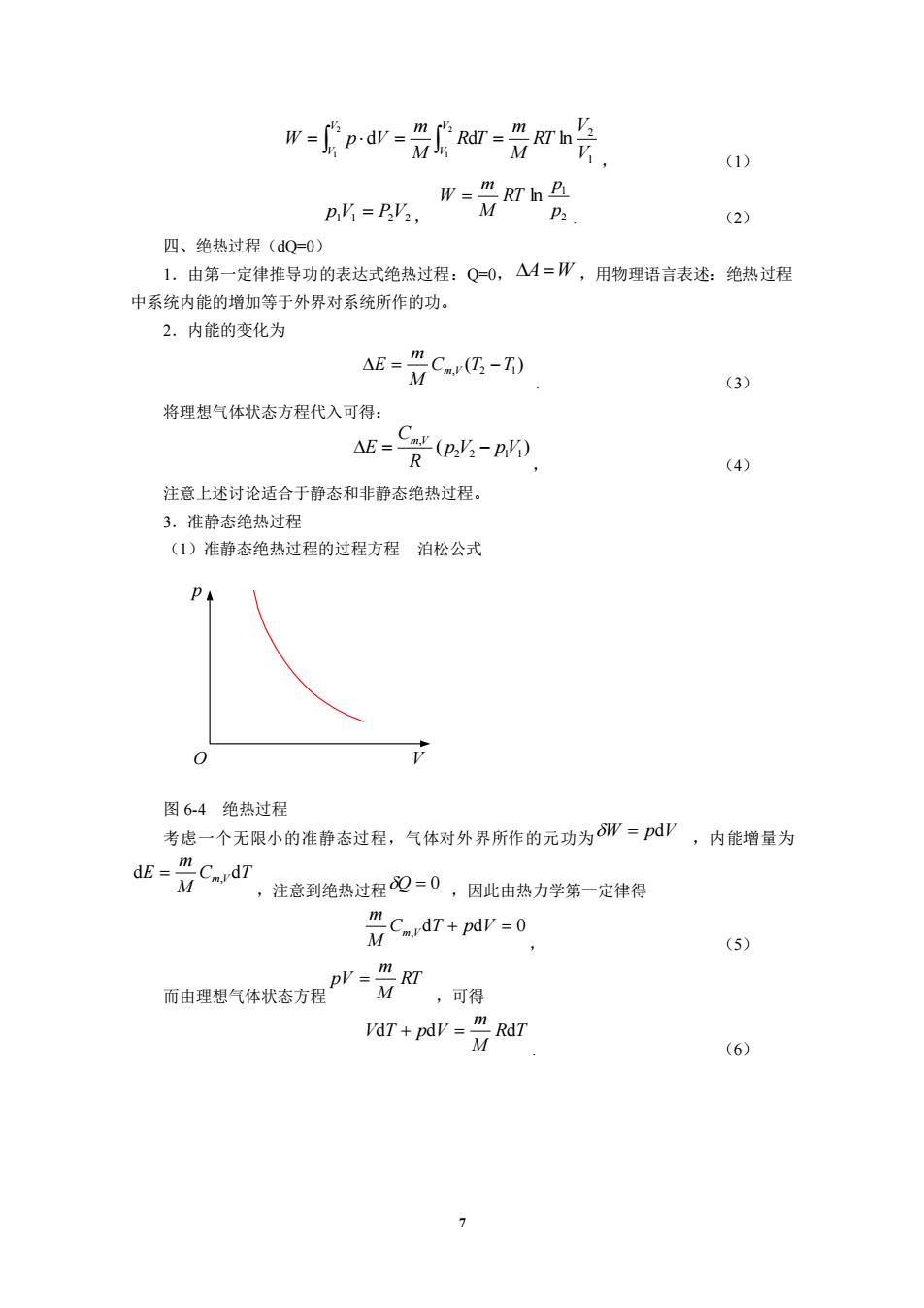
7 1 2 d d ln 2 1 2 1 V V RT M m R T M m W p V V V V V = = = , (1) p1V1 = P2V2 , 2 1 ln p p RT M m W = . (2) 四、绝热过程(dQ=0) 1.由第一定律推导功的表达式绝热过程:Q=0, A =W ,用物理语言表述:绝热过程 中系统内能的增加等于外界对系统所作的功。 2.内能的变化为 ( ) C , T2 T1 M m E = m V − . (3) 将理想气体状态方程代入可得: ( ) 2 2 1 1 , p V pV R C E m V = − , (4) 注意上述讨论适合于静态和非静态绝热过程。 3.准静态绝热过程 (1)准静态绝热过程的过程方程 泊松公式 p O V 图 6-4 绝热过程 考虑一个无限小的准静态过程,气体对外界所作的元功为 W = pdV ,内能增量为 C T M m dE = m,V d ,注意到绝热过程 Q = 0 ,因此由热力学第一定律得 C , dT + pdV = 0 M m m V , (5) 而由理想气体状态方程 RT M m pV = ,可得 R T M m VdT + pdV = d . (6)