
Deterministic radio propagation modeling and ray tracing Introduction to deterministic propagation modelling 2) Geometrical Theory of Propagation I-The ray concept-Reflection and transmission 3) Geometrical Theory of Propagation II-Diffraction,multipath 4) Ray Tracing I 5) Ray Tracing II-Diffuse scattering modelling 6) Deterministic channel modelling I 7) Deterministic channel modelling II-Examples 8) Project discussion
1 Deterministic radio propagation modeling and ray tracing 1) Introduction to deterministic propagation modelling 2) Geometrical Theory of Propagation I - The ray concept – Reflection and transmission 3) Geometrical Theory of Propagation II - Diffraction, multipath 4) Ray Tracing I 5) Ray Tracing II – Diffuse scattering modelling 6) Deterministic channel modelling I 7) Deterministic channel modelling II – Examples 8) Project - discussion
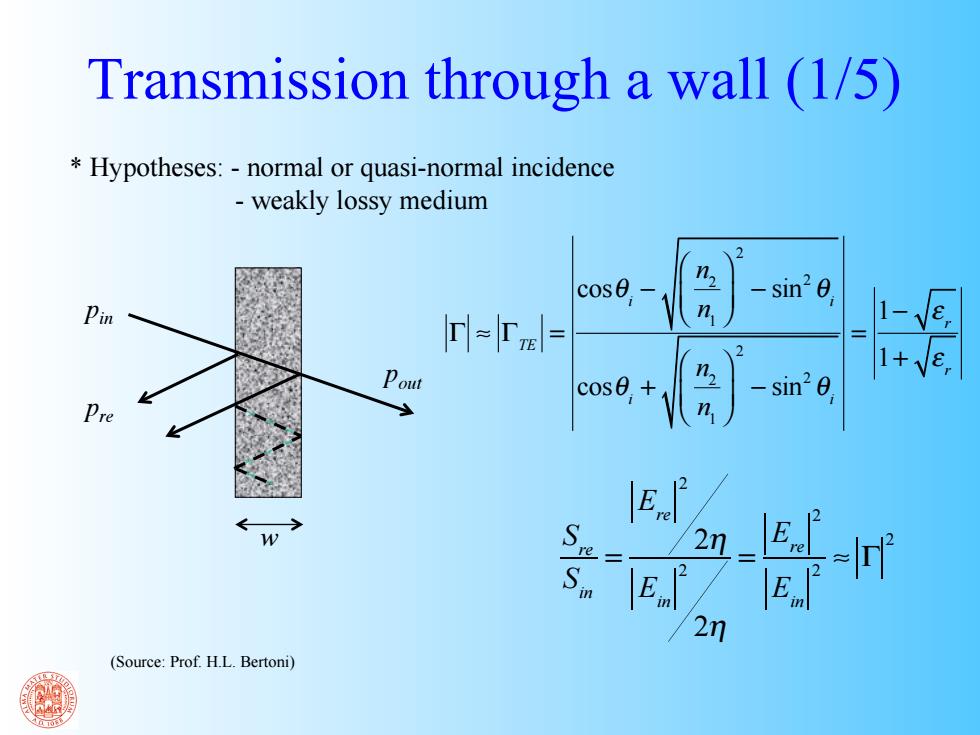
Transmission through a wall (1/5) Hypotheses:-normal or quasi-normal incidence -weakly lossy medium cos0, sin20 Pin n 1 rl-Til= Pout n 1+√e sin20, Pre 2n_ E 2n (Source:Prof.H.L.Bertoni)
Transmission through a wall (1/5) S re Sin = E re 2 2η Ein 2 2η = E re 2 Ein 2 ≈ Γ 2 pin pre pout (Source: Prof. H.L. Bertoni) * Hypotheses: - normal or quasi-normal incidence - weakly lossy medium Γ ≈ ΓTE = cosθi − n2 n1 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 − sin2 θi cosθi + n2 n1 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 − sin2 θi = 1− ε r 1+ ε r w

Transmission through a wall (2/5) In a lossy medium the wavenumber can be written as: k=ωVoee=0√40e0, The complex relative dielectric constant can be written as: ,=e,-je=-j0 E0E0 If the medium is weakly lossy e"<<'. A plane wave propagating through the lossy medium has the expression: E=Ege=Epe(+);with jk-@tjB Thus: 到 Where the series expansion have been truncated at first order
Transmission through a wall (2/5) k = ω µ0ε c = ω µ0ε 0ε r ε r = ε r ′ − jε r ′′ = ε ε 0 − j σ ωε 0 E = E0e− jkr = E0e −(α + jβ )r ; with jk=α+jβ k = ω µ0ε 0ε r = ω µ0ε 0 ε r ′ − jε r ′′ = ω c ε r ′ − jε r ′′ = = ω c ε r ′ 1− j ε r ′′ ε r ′ ≈ ω c ε r ′ 1− j ε r ′′ 2ε r ′ ⎛ ⎝ ⎜ ⎜ ⎞ ⎠ ⎟ ⎟ In a lossy medium the wavenumber can be written as: The complex relative dielectric constant can be written as: If the medium is weakly lossy ε ” << ε ’. A plane wave propagating through the lossy medium has the expression: Thus: Where the series expansion have been truncated at first order

Transmission through a wall (3/5) Therefore: a-av Er=E0e“ S(r)=S(0).e-2r
Transmission through a wall (3/5) jk = α + jβ ≈ ω c ε r ′ ε r ′′ 2ε r ′ + j ⎛ ⎝ ⎜ ⎜ ⎞ ⎠ ⎟ ⎟ ⇒ α ≈ ω c ε r ′ ε r ′′ 2ε r ′ ⎛ ⎝ ⎜ ⎜ ⎞ ⎠ ⎟ ⎟ β ≈ ω c ε r ′ ⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪ Therefore: E(r) = E(0) ⋅ e−αr S(r) = S(0)⋅ e−2αr

Transmission through a wall (4/5) The reflection coefficient at normal incidence for the air-medium interface is 1+Ve, The reflection coefficient for the second,medium-air interface is(see the expression of the reflection coefficients for normal incidence) Tno=ve-1 1+Ve, =-T0m Now if we consider the first interface we have 1En月
Transmission through a wall (4/5) 0 1 1 r m r ε ε − Γ = + 0 0 1 1 r m m r ε ε − Γ = = −Γ + Srefl1 Sinc1 = Erefl1 2 Ein1 2 = Γ0m 2 The reflection coefficient at normal incidence for the air-medium interface is The reflection coefficient for the second, medium-air interface is (see the expression of the reflection coefficients for normal incidence) Now if we consider the first interface we have