
3-6功能原理机械能守恒定律 第三章动量守恒定律和能量守恒定律 Pcos0. 已知h=50m,4=0.050,s'=500m, 求S 解以雪橇、冰道和地球为一系统,由功能原理得 Ws=E2-E W:=-umg cos0s'-umgs -Lmg(s'+s) 又 E,-E =-mgh
3-6功能原理 机械能守恒定律 第三章动量守恒定律和能量守恒定律 FN Ff P Psin Pcos h s' 已知 h = 50m , = 0.050 , s' = 500m , 求 s. 解 以雪橇、冰道和地球为一系统,由功能原理得 Wf = E2 − E1 cos ' ( ' ) f W = −mg s −mgs −mg s +s E − E = −mgh 又 2 1
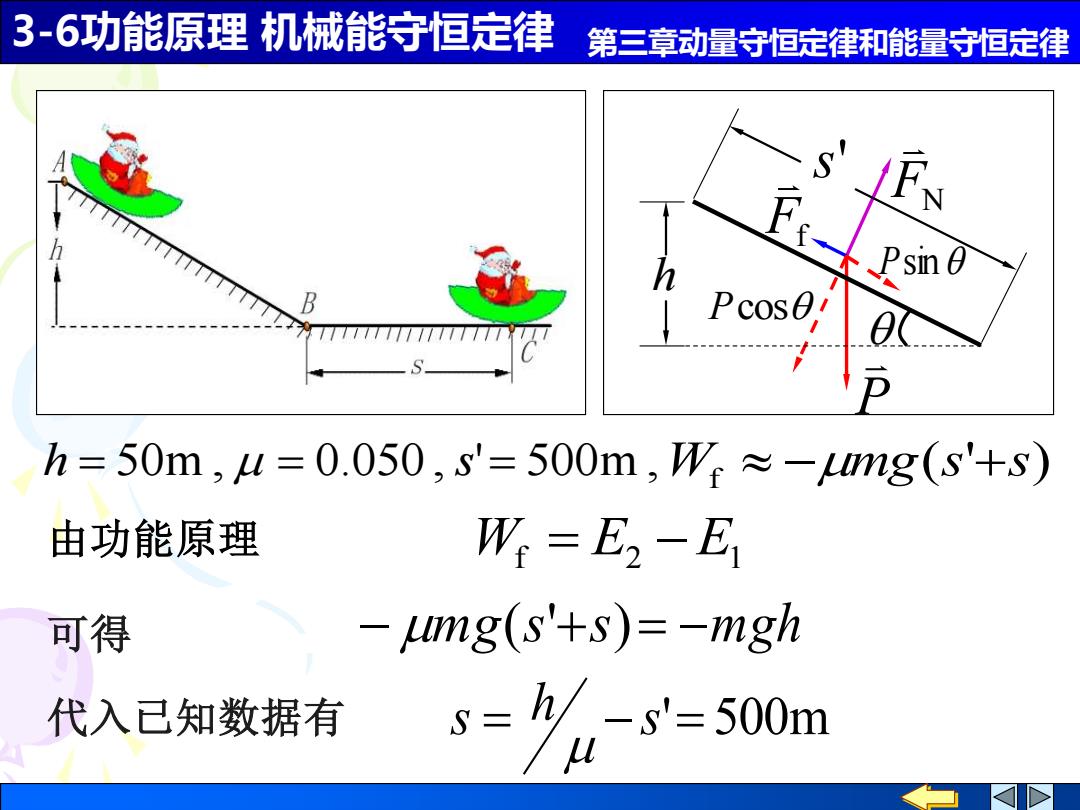
3-6功能原理机械能守恒定律 第三章动量守恒定律和能量守恒定律 B h=50m,4=0.050,s'=500m,W≈-mg(s'+s) 由功能原理 Wr=E2-E 可得 -umg(s'+s)=-mgh 代入已知数据有 s=-s'-500m
3-6功能原理 机械能守恒定律 第三章动量守恒定律和能量守恒定律 可得 − mg(s'+s)= −mgh FN Ff P Psin Pcos h s' 由功能原理 Wf = E2 − E1 s = h − s' = 500m 代入已知数据有 h = 50m , = 0.050 , s' = 500m , ( ' ) f W −mg s +s
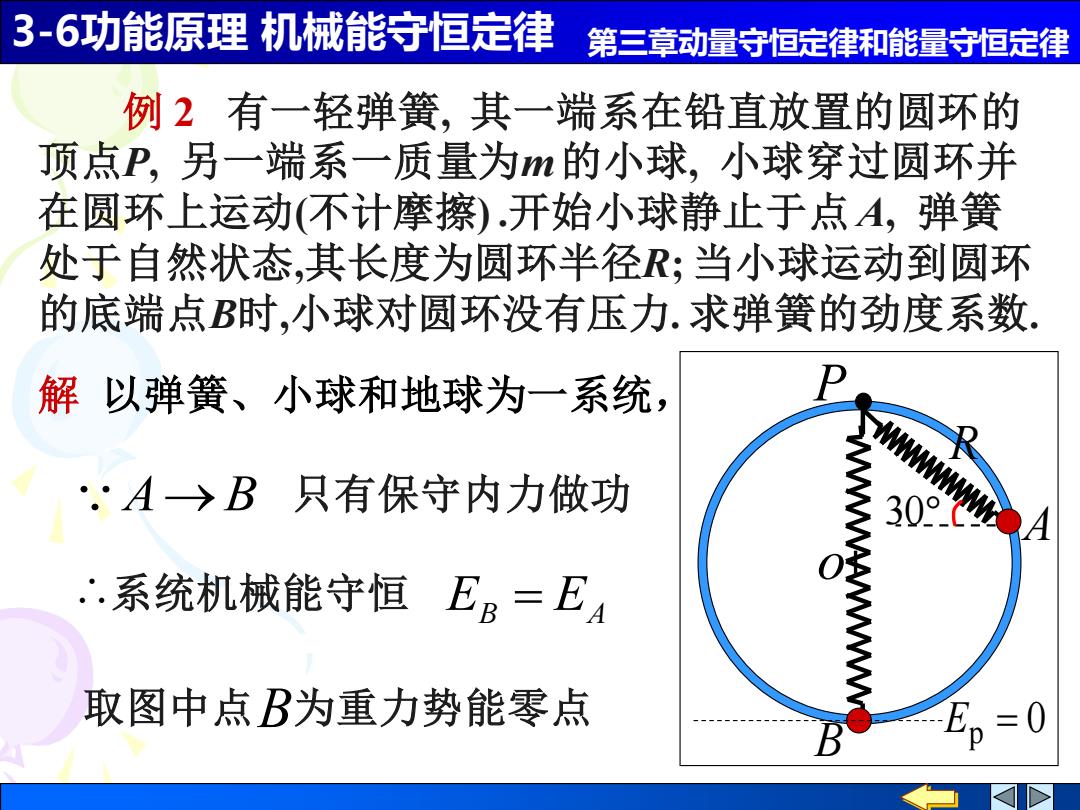
3-6功能原理机械能守恒定律 第三章动量守恒定律和能量守恒定律 例2有一轻弹簧,其一端系在铅直放置的圆环的 顶点P,另一端系一质量为m的小球,小球穿过圆环并 在圆环上运动(不计摩擦).开始小球静止于点A,弹簧 处于自然状态,其长度为圆环半径R;当小球运动到圆环 的底端点B时,小球对圆环没有压力.求弹簧的劲度系数, 解以弹簧、小球和地球为一系统, .·A→B只有保守内力做功 系统机械能守恒EB=E4 取图中点B为重力势能零点 =0
3-6功能原理 机械能守恒定律 第三章动量守恒定律和能量守恒定律 例 2 有一轻弹簧, 其一端系在铅直放置的圆环的 顶点P, 另一端系一质量为m 的小球, 小球穿过圆环并 在圆环上运动(不计摩擦) .开始小球静止于点 A, 弹簧 处于自然状态,其长度为圆环半径R; 当小球运动到圆环 的底端点B时,小球对圆环没有压力. 求弹簧的劲度系数. 解 以弹簧、小球和地球为一系统, 30 o P B R A A→B 只有保守内力做功 系统机械能守恒 EB = EA 0 取图中点B为重力势能零点 Ep =
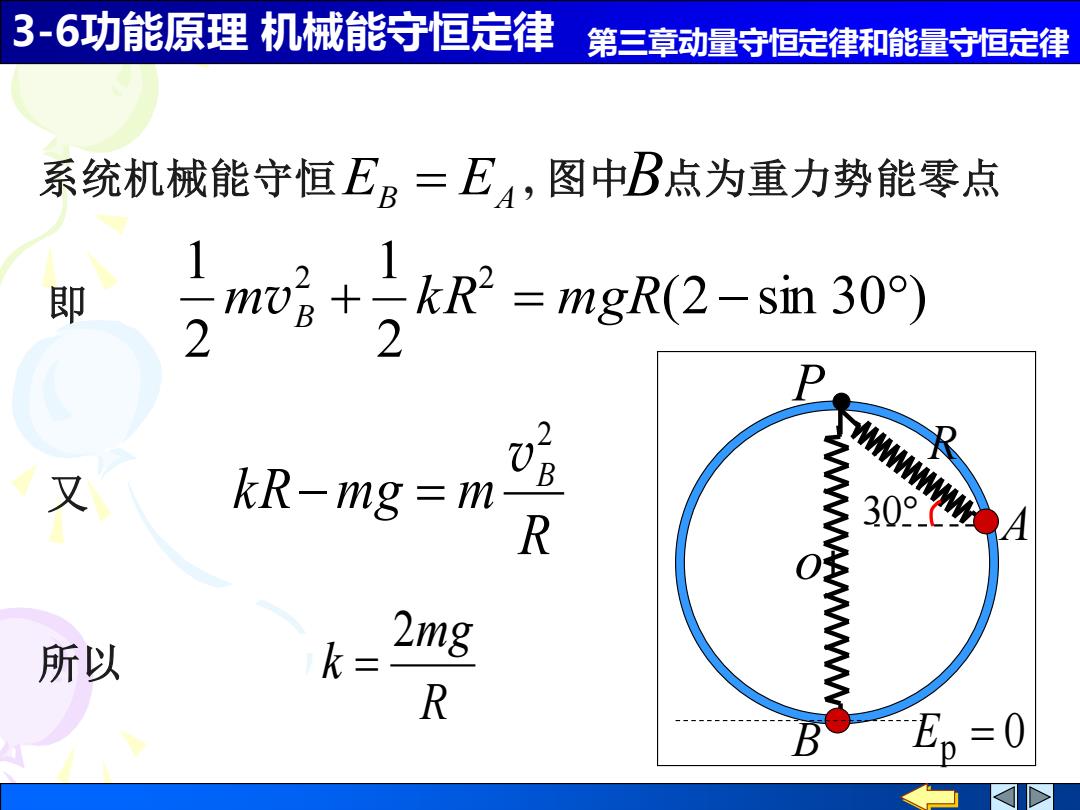
3-6功能原理机械能守恒定律 第三章动量守恒定律和能量守恒定律 系统机械能守恒EB=E4,图中B点为重力势能零点 即 mgR(2-sin 30) 2 又 kR-mg =m R 30° 所以 k= 2mg R E,=0
3-6功能原理 机械能守恒定律 第三章动量守恒定律和能量守恒定律 又 R k R mg m B 2 v − = 所以 R mg k 2 = 即 (2 sin 30 ) 2 1 2 1 2 2 m + k R = mgR − vB 30 o P B R A 0 Ep = 系统机械能守恒 EB = EA , 图中 B 点为重力势能零点