
2流体的pVT关系19 z=1+号+号+是+(时)e即() (2-48) 其中 B=b1-b2/T,-b3/T-b4/T (2-49a) C=-c2/T,+c3/T (2-49b) D=d1十d2T. (2-49c) 简单流体的状态方程中的常数由Ar、Kr和CH的实验数据计算而得,参考流体选择正 辛烷,?及其相应的状态方程中的常数值是经过对其他物质压缩因子和热力学数据拟合、调 整后得到。两种流体的状态方程常数示于表2-6。 表2-6式(2-481中的常数 常数 简单流体 参考流休 常数 简单流体 参考流体 0.118119 0.2026579 0.0 0.01690 0.26572 0.33151 0.0427 0.04157 0.15479 0.0276 a8 0.0186984 0.0503618 0.060167 0.03754 【例2-3】用Pitzer的普遍化关系式计算甲烷在323.16K时产生的压力。已知甲烷的摩尔 体积为1.25×10-4m3/mol,压力的实验值为1.875×10Pa。 解从附录二查得甲烷的临界参数为 T.=190.6K,p,=4.600MPa,u=0.008 因此T,=323.16/190.6=1.695;力,不能直接计算,需迭代求解。 p=ZRT/V=Z×8.314×323.16/1.25×10-4=2.149×107z 而 p=p力,=4.600×10p, 4.600×106 因此 Z-=2i49x10,=0.214p, (A) 据式(2-46) Z=Z+21 (BY 设Z值代人式(A)求出p,:根据T、p,值查附录三表A1和表A2得和2,再将2、Z代人式 (B)求得Z值。比较Z的计算值与假设值,如相差较大则代入式(A)重新计算,直至迭代收敛。 迭代的结果为 p.=4.06时,Z=0.877 p=ZRT/V=0.877×8.314X323.16/1.25×10-4=1.885×107Pa 误差 (1.875-1.885)×102/1.875×107=-0.5% 2.3.3普遍化状态方程 用对比参数T,、p,、V,代替变量T、p、V,消去状态方程中反映气体特征的常数,所得 的方程称为普遍化状态方程。原则上它适用于任何气体。前面介绍的van der Waals的简单对 比态原理式(2-44)和Lee-Kesler方程式(2-47)均是普遍化状态方程的例子。 以下介绍Pitzer提出的普遍化第二Virial系数关系式。该式是一个解析计算式,计算时不 需要查图,在工程应用中受到欢迎。 将T=T.T.,p=p,p.代入舍项Virial方程(2-28a)中得到 z=1+器=1+()) (2-50) 变量()是无量粥的,可以看成对比第二里系数。对于指定的气体来说,B仅仅是温度
叫川关系| B I C I D I C4 f" I Y \ f Y \ Z=l+ 一+一十一+一一一(卢十一) exp ( - T 2 ) (2-48) Vr viv:T vf /XP } 其中 B=b 一句 -b3 T; (2-49a) C=c)-czlTr+C3/T; (2-49 b) +的 (2-49c) 流体的状态方程中的常数由 Ar Kr CH 的实验数据计算而得, 参考流体选择正 辛烧 zr 及其相应的状态方程中的常数值是经过对其他物质压缩因子和热力学数据拟 、调 整后得到 两种流体的状态方程常数示于表 2-6 2-6 (2-48) 中的常数 常数 简单流体 参考流体 常数 简单流体 参考流体 b1 0. 1181193 0. 20265 79 C3 0.0 0.0 16901 b2 0.265728 0.3315 11 C. 0.042 724 0.041577 b3 0.154790 0. 027655 d1 X10' O. 155488 0.48736 b, 0. 030323 O. 203488 d2 X10' O. 623689 0.0740336 C1 0. 0236744 0.0313385 R O. 65392 1. 226 C2 0.0186984 0. 0503618 Y 0.060167 0.03754 [01J 2-3> Pitzer 的普遍化关系式计算甲皖在 32 .1 产生的压力。 已知甲 烧的摩尔 体积为1. 25 lO 3/ mo ,压力的实验值为1. 875 X 107 Pa 从附录二查得甲炕的临界参数为 =190.6K =4.6OOMPhω=0.008 因此 =323.16 190. 6= 1. 695;ρz 不能直接计算,需迭代求解。 ZRT y=Z . 314 X 323.16/ 1. 25 X 10 - 4 =2.149 X 107 Z P=P ρr=4.600 06ρr 4. 600 X 106 因此 Z= =0 214ρ (A) 2. 149 X 107Yr v . ~~.Y 据式 (2 46) Z=Zo ωZ ) (B) 值代入式(A) 求出 ρr; 根据 ρr 值查附录三表 和表 AZ 21; 再将 ZJ 代人式 (8)求得 比较 的计算值与假设值,如相差较大则代入式 (A) 重新计算,直至迭代收敛 选代的结果为 Pr =4.06 Z=O. 877 =ZRT =O . 877 X 8. 314 X3 23.16 / 1. 25 X 10- 4 = 1. 885 X 107 Pa (1. 875 - 1. 885) X 107 / 1. 875 X 107 = - 0. 5% 2.3.3 普遍化状态方程 用对比参数 代替变量 ,消去状态方程中反映 体特征的常数,所 的方程称为普遍化状态方程 原则上它适用于任何气体。前面介绍的 van der Waals 的简 态原理式 (2-44) Lee-Kes er 方程式 (2-47) 均是普遍化状 方程的例子 以下介绍 Pitzer 提出的普遍化第二 Viri 系数关系式。该式是一个解析计算式,计算时不 查图,在工程应用中受到欢迎。 T=TrT P=PrP 代入舍项 Virial 方程 (2-28a) 中得到 B 1J . , f Bp^ \ ρL Z=l +;:-!;:.=1 + 11 ~r 1 (2-50) RT ~'\ RTcl J fB ρx 变量 一一旦 是无量纲的,可以看成对比第二维里系数 对于指定的气体来说 仅仅是温度 \RTcJ

20化工热力学 的函数,B的普遍化关系只与对比温度有关,而与对比压力无关。因此,Pitzer提出了如下的 关联式 BP:-B+oB (2-51) 式中,B和B只是对比温度的函数,用下述关系式表示 B0=0.083-0.422/T.8 (2-52a) B=0.139-0.172/T2 (2-52b) 以后Tsonopoulos°又将Pitzer的关联式修改为 B0=0.1445-0.330/T,-0.1385/T-0.0121/T-0.000607/T B1=0.0637+0.331/T2-0.423/T-0.008/T 上述关系式适用范围位于图2-8所示曲线上面 普海化维里系数使用 的区域。该线是根据对比体积V,≥2绘制的。当对 比温度高于T=4时,则对压力没有什么限制,但 是须V.≥2。对于较低的对比温度,允许的压力范 普化压因子使用 围随着温度的降低而降低。但在对比温度约为0.9 这一点以前,压力范围则受饱和(冷凝)蒸气压的 2 5 6 限制。图28的虚线表示饱和线。图28曲线以下 的条件范围内,适用Pitzer提出的压缩因子关系式 图28普遍化关系式适用区域 (2-46)。 【例2-4】质量为500g的氨气贮于容积为0.03m3的钢弹内,钢弹浸于温度为65℃的恒温 浴中。试用普遍化第二Virial系数计算氨气压力,并与文献值p=2.382MPa比较。 解从附录二查得氨的临界参数 T.=405.6K,p.=11.28MPa,V.=72.6×10-6m3/mol,w=0.250 求氨的摩尔体积 V010-m/mol V-2102-141 由于V,>2,故适用普遍化第二Virial系数关系式。 T,=338.15/405.6=0.834 B0=0.083-0.422/(0.834)6=-0.481 B=0.139-0.172/(0.834)42=-0.230 由式(2-51) 2=+81=-041-250Xa.230=-580 所以 B=-0.539×8.314×405.6 11.28×105 -1.611×10-4m3/mol 由式(2-50)》 z-器-1+器 Tsonopoulos C.AIChEJ,1974,20:263
耀黯 |化工热力学 的函数 的普遍化关系只与对比温度有关,而与对比压力无关。因此, Pitzer 提出了如下的 关联式 Bρ . 一:.,_ = Bo ,ß l RTc 式中 只是对比温度的函数,用下述关系式表示 (2-51 ) BO=0.0830.422/ T:6 B1 =0.139-0. 172/ :r;.2 以后 Tsonopoulos 又将 Pitzer 的关联式修改为 BO =0.1445 .3 30 o. 1385/ T; -0. 012l/T; -0.00060 Bl = 0.0637+0. 331/T; - 0. 423 T; 0.008 上述关系式适用范围位于图 -8 所示曲线上面 的区域 。该线是根据对比体积 二三 绘制的 当对 比温度高于 =4 时,则对压力没有 么限制,但 是须 对于较低的对比温度,允许的压力范 围随着温度的降低而降低 但在对比温度约为 9 这一点以前,压力范围则受饱和(冷凝)蒸气压的 8 限制 2-8 的虚线表示饱和线 曲线以 的条件范围内,适用 Pitz 提出的压缩因子关系式 (2-52a) (2-52 b) 4 ,. 3 E-," 2 2 3 普遍化关系式适用区域 (2 46) 【例 2-4 500g 的氨气贮于容积为 .03 的钢弹内,钢弹浸于温度为 65 的恒温 浴中。试用普遍 irial 系数计算氨气压力 并与文献值 2. 382MPa 比较 解从附录二查得氨的临界参数 Tc=405.6K , 求氨的摩尔体积 p c=11.28MPh VC =72. 6× 10- 6mV m01 , ω=0.250 O. 03 一一一 1. 021 X 10- 3m3 / mol 500/ 17.02 V1.021 × 10-3 = ~:._ -~ .'_~.~ ^ = 14. 1 72.6 X 10- Ö 由于 >2 故适用普遍化第二 Viri 系数关系式 Tr = 338.15/ 405.6 = 0.834 BO 0.083 0. 422 (0 834) 1. 0. 481 Bl = 0. 139 o. 172/ (0. 834)4. 2 = - 0. 230 由式 (2-51) 所以 由式 (2-50) Bρ :.,_ = BO ωBl= 481 O. 250 X O. 230 539 RTc 0. 539 X 8. 314 X 405. 6 B= - V , vvv,/,' V~AV ', "'vv , V = -1. 611 X 10- 4 m3 / mol 11. 28 X 10ö P -TA B + R - v - T -P R - Z Tso opoulosC.AIChEj 1974 , 20: 263

2流体的pVT关系21 则 计算值与实验值2.382MPa是非常接近的,说明在压力不太高时,普遍化第二Virial系数 用于极性物质广度性质计算,结果也较满意 【例2-5】试将以下形式的RK方程改写成普遍化形式,并计算277.6K,4.513×105P 时乙烯的摩尔体积。 (A) 其中 h=B/Z,B=bp/RT,A/B=a/bRT1.5 (B) 式中,a、b为RK方程的常数。 解 ①将a=0.42748R2T25/p,b=0.08664RT./p.,T=T,T,p=p,P.代入式 (B),得 B=0.08664./T,A/B=4.9340/T. 所以普遍化RK方程为 z亡4(年) (C) 其中 h=0.086642 (D) ZT. ②从附录二查得乙烯临界参数 T.=282.4,p.=5.036MPa 因此将T,=277.6/282.4=0.983,p,=4.513×10°/5.036×108=0.896代入式(C)、式 (D),整理得 1 Z=1已A5.0625(+6 (E) h=0.07897/Z (F) 由式(E)、式(F)迭代求解得Z=0.4882,乙烯的摩尔体积V=ZRT/p=0.4882×8.314× 277.6/4.513×10=2.497×10-4m3/mol,与实验值V=2.43×10-4m3/mol比较,误差 为2.8%。 2.4真实气体混合物的pV-T关系 化工生产中,处理的物系往往是多组分的真实气体混合物。目前虽然已收集、积累了许多 纯物质的pVT数据,但混合物的实验数据很少,不能满足工程设计的需要。解决这一问题 的有效方法是在纯组分性质和混合物性质之间建立起联系,用纯物质性质来预测或推算混合物 性质。描述纯物质性质和混合物性质之间联系的函数式称为混合规则。纯气体的pVT关系 式借助于混合规则便可推广到气体混合物。 2.4.1混合规则与虚拟临界参数 目前使用的混合规则绝大部分是经验的,是从大量实际应用中总结归纳后建立起来的。其 中典型的混合规则表达式为 Qm=∑∑yy,Q (2-53) 式中,Q表示混合物性质,可以是临界参数T。、p。、V。,也可以是偏心因子u等其他 参数:y是混合物中各组分的摩尔分数:Q,当下标相同时表示纯组分性质,下标不同时表示
2 jrV 关系| RT 8. 314 X 338. 15 ρ= 一一一-~- 吨, ;-:-::-;- = 2. 378 X 106 Pa r V-B 计算值与实验值 2.382MPa 是非常接近的,说明在压力不太高时,普遍化第二 Virial 系数 用于极性物质广度性质计算,结果也较满意 【例 2-5 试将以下形式的 RK 方程改写成普遍化形式,并计算 277.6K 4.513 10 Pa 时乙烯的摩尔体积。 A-B h-m -H Z (A) 其中 h=B/ Z , B=bp/RT, A / B=a/ bRT1. 5 (B) 式中 RK 方程的常数。 ①将 = O. 42748R2 T2. 5/ b = O. 08664RT 式, T=TrTc ' P=PrP 代人式 (B) ,得 B=0.08664 B=4. 9340/ T;' 5 所以普遍化 RK 方程为 其中 一十4. 3~0 (~ì 1- h T l. h) O. 08664ρ- h=-一-一一.:. ZTr (C) (D) 从附录二查得乙烯临界参数 =282.4 c=5.036MPa 因此将 Tr 277.6/2 82 0.983 pr=4.513 106 5.036 106= 896 代人式 (C) (D) ,整理得 nu po -H Z (E) h= 0.07897/Z (F) 由式(E)、式 (F) 迭代求解得 0.4882 ,乙烯的摩尔体积 ZRT O. 4882 X 8.314 X 277.6/4. 513 X 106 = 2. 497 X 10- 4 m3 mol ,与实验值 = 2. 43 X 10- 4 mol 比较,误 2.8% 2.4 真实气体混合物的 p- V-T 关系 工生产中 ,处理的物系往往是多组分的真实气体泪合物。目前虽然已 、积累了许 纯物质的 jrV-T 数据,但混合物的实验数据很少,不能满足工程设计的需要 解决这一问题 的有效方法是在纯组分性质和混合物性质之间建立起联系,用纯物质性质来预测或推算泪合物 性质 描述纯物质性质和混合物性质之间联系的函数式称为混合规则 纯气体的 jrV 关系 式借助于混合规则便可推广到气体混合物。 2.4.1 混合规则与虚拟临界参数 目前使用的混合规则绝大部分是经验的,是从大量实际应用中总结归纳后建立起来的 中典型的混合规则表达式为 Qm = .2: .2: y iy j Qij (2 式中, Qm 表示混合物性质,可以 临界 也可以是偏心因 等其他 是混合物中各组分的摩尔分数 ij 下标相同时表示纯组分性质,下标不同时

22化工热力学 相互作用项,相互作用项Q,代表了混合过程引起的非理想性。 如何求取Q,对混合规则有很大影响,通常采用算术平均或几何平均来计算。 若取算术平均 Q=(Q:+Q)/2 则式(2-53)变为 Qm-∑y.Q (2-54) 若取几何平均 Qi=(Q:Qi)0.5 则式(2-54)变为 Qm=(∑,Qg5)月 (2-55) 一般情况,算术平均用于表示分子大小的参数,几何平均用于表示分子能量的参数 将混合物视为假想的纯物质,具有虚拟临界参数,就可以把纯物质的对比态方法应用到混 合物上。Kay提出的最简单的混合规则将混合物虚拟临界参数表示为 Tm=∑y,Ta,pm=∑y,pa (2-56) 式中,Tm )为虚拟临界温度和压力:y.为组分五的摩尔分数。 求得虚拟临界参数后,混合物即可作为假想的纯物质进行计算。 若混合物中所有组分的临界温度和压力之比在以下范围内 0.5<T/Tg<2,0.5<pa/pg<2 Kay规则与其他较复杂的规则比较,计算Tm值的差别小于2%。 对于虚拟临界压力,除非所有组分的p。或V。都比较接近,否则式(256)的计算结果通 常不能令人满意。为此Prausnitz和Gunn●提出了一个改进的表达式 pm=R(∑yZi)Tm/∑y,Ve (2-57) 式(2-56)和式(257)中都不含有组分间的相互作用项,因此这些混合规则不能直正反映 混合物性质。对于组分差别很大的混合物,尤其是含有极性组分或有缔合成二聚体倾向的体 系,这些混合规则不能适用。 2.4.2气体混合物的第二Virial系数 由统计力学可以导出气体混合物第二Virial系数为 B=∑∑yy,Bg (2-58) 这是少数从理论推导的混合规则之一。 式中,y代表混合物中各组分的摩尔分数:B,表示组分i和j之间的相互作用,i和j相 同,表示同类分子作用,i和j不同,表示异类分子作用,且B=B:。 对于二元混合物,式(2-58)展开为 B=yB1+2y1y,B12十y2B2 (2-59) 式中,B1、Bz2是纯物质1和纯物质2的第二Virial系数;B,代表混合物性质,称为交 叉第二Virial系数,它们都只是温度的函数。 纯物质第二Virial系数可按式(2-5l)计算,交叉第二Virial系数按以下的经验式计算 B-RT(B+gB) (2-60) 式中,B和B是如同式(2-52a)、式(252b)一样的对比温度T,的函数 Prausnitz对计算Tw、p和wu提出如下的混合规则 T=(T.T)5(1-k) (2-61) Prausnitz J M,Gunn R D.AIChE J,1958,4(430):494
|化工热力学 相互作用项,相互作用项 Qij 代表了混合过程引起的非理想性 如何求取 Qi 对混合规则有很大影响,通常采用算术平均或几何平均来计算 若取算术平均 Qij = (Qii jj) / 2 则式( 2-53) 变为 Qm = I: y ;Q i (2-54) 若取几何平均 Qij = (Qii Q jj ) O. 5 则式 (2-54) 变为 Qm = (I: ~.5 2 (2 -55) 一般情况,算术平均用于表示分子大小的参数,几何平均用于表示分子能量的参数。 将?昆合物视为假想的纯物质,具有虚拟临界参数,就可以把纯物质的对比态方法应用到 合物上。 Kay 提出的最简单的混合规则将混合物虚拟临界参数表示为 T cm I: y ;T c;. Pcm - I: 式中 cm ρm 为虚拟临界温度和压力 y; 为组分 的摩尔分数。 求得虚拟临界参数后,混合物即可作为假想的纯物质进行计算。 昆合物中所有组分的临界温度和压力之比在以下范围内 5<T /Tcj <2. 0.5<ρ <2 Kay 规则与其他较复杂的规则比较,计算 cm 值的差别小于 (2-56 ) 对于虚拟临界压力,除非所有组分的户或 都比较接近,否则式 (2-56) 的计算结果通 常不能令人满意。为此 Prausnitz Gunn 提出了一个改进的表达式 Pcm = R (I: y;Zc; )Tcm / I: yy (2 57) (2-56 )和式 (2-57) 中都不含有组分间的相互作用项,因此这些混合规则不能真正反映 混合物性质 对于组分差别很大的混合物,尤其是含有极性组分或有缔合成二聚体倾向的体 系,这些混合规则不能适用 2.4.2 气体混合物的第二 Virial 系数 由统计力学可以导出气体混合物第二 Virial 系数为 B = I: I: ;j (2-58) 这是少数从理论推导的混合规则之一 式中 代表泪合物中各组分的摩尔分数 B;j 表示组分 之间的相互作用. 同,表示同类分子作用. 不同,表示异类分子作用,且B;j =B 对于二元泪合物,式 (2 -58 展开为 B= y~ Bll 2YjY2B12 +y;B22 (2-59) 式中 Bll 是纯物质 和纯物质 的第二 Virial 系数 B;j 代表混合物性质,称为交 叉第二 Virial 系数,它们都只是温度的函数 纯物质第二飞Tirial 系数可按式 (2-51 )计算,交叉第二 Virial 系数按以下的经验式计算 RT, . ,= 兀立(B ;jBl) ω0) 式中 BO Bl 是如同式 (2 -52 a) 、式 (2-52b) 一样的对比温度 的函数。 Prausnitz 对计算 町、丸。和 ω1) 提出如下的混合规则 Tc;j=( )O.5 (1走。) (2-61) o Prausnitz J M , Gunn R D. AIChE J, 1958 , 4(430) :494
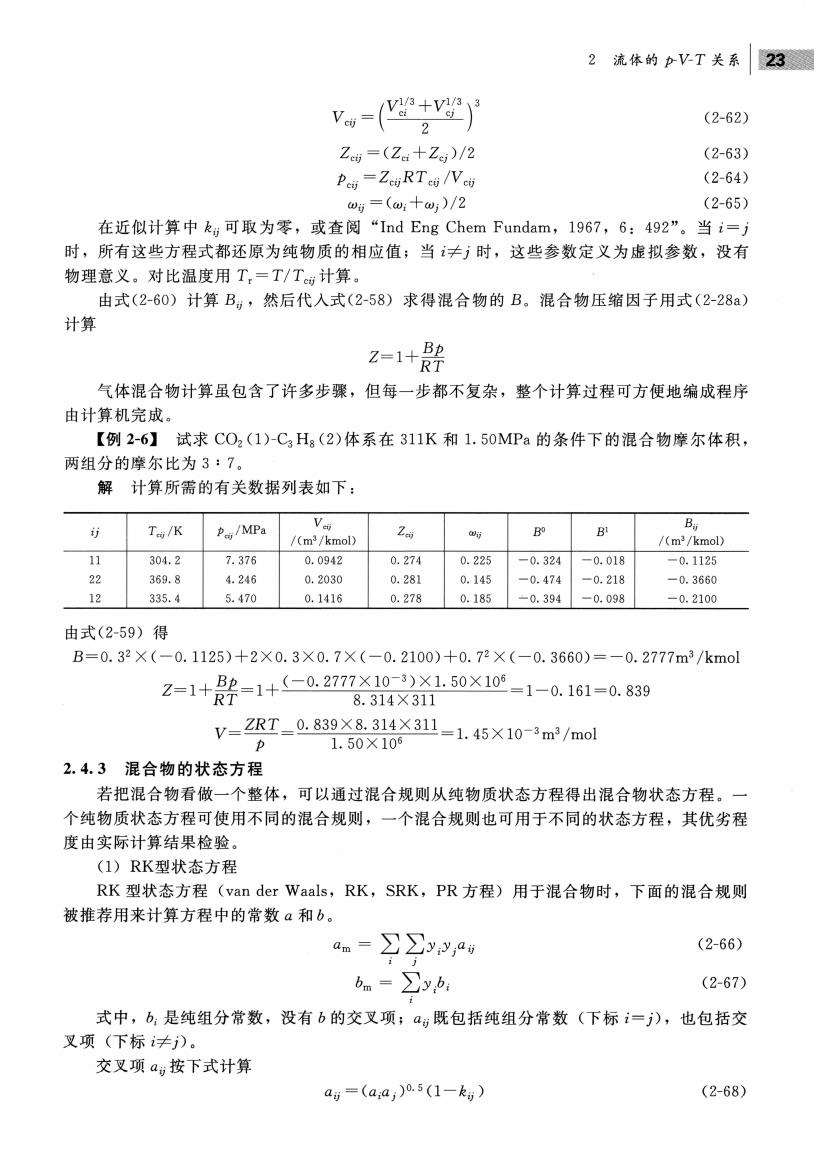
2流体的pVT关系23 V(+v (2-62) Ze=(Za+Zg)/2 (2-63) Pe=ZcgRTeg /Ve (2-64) :=(w:十w:)/2 (2-65) 在近似计算中k可取为零,或查阅“Ind Eng Chem Fundam,1967,6:492”。当i=j 时,所有这些方程式都还原为纯物质的相应值;当≠时,这些参数定义为虚拟参数,没有 物理意义。对比温度用T,=T/T计算 由式(2-60)计算B,然后代入式(2-58)求得混合物的B。混合物压缩因子用式(2-28a) 计算 =1+ 气体混合物计算虽包含了许多步骤,但每一步都不复杂,整个计算过程可方便地编成程序 由计算机完成。 【例2-6】试求CO,(1)-CH。(2)体系在311K和1.50MPa的条件下的混合物摩尔体积, 两组分的摩尔比为3:7。 解计算所需的有关数据列表如下 T/K /MPa /(m/kmol) B B /(m/kmol) 11 304.2 7.376 0.0942 0.274 0.225 -0.324-0.018 -0.1125 22 369.8 4.24 0.2030 0.281 0.145 0.474 -0.218 -0.3660 12 335.4 5.470 0.1416 0.278 0.185 -0.394 -0.098 -0.2100 由式(2-59)得 B=0.32×(-0.1125)+2×0.3×0.7×(-0.2100)十0.72×(-0.3660)= -0.2777m3/kmol 2=1+影=1+-0.277X301.50×10-1-0.161-0.839 8.314×311 v=Zr-089X8X31-1.45×10m/ml 2.4.3混合物的状态方程 若把混合物看做一个整体,可以通过混合规则从纯物质状态方程得出混合物状态方程。 个纯物质状态方程可使用不同的混合规则,一个混合规则也可用于不同的状态方程,其优劣程 度由实际计算结果检验 (1)RK型状态方程 RK型状态方程(van der Waals,RK,SRK,PR方程)用于混合物时,下面的混合规则 被推荐用来计算方程中的常数a和b。 d.->ypau (2-66) bm=∑yb (2-67) 式中,b:是纯组分常数,没有b的交叉项;ag既包括纯组分常数(下标i=j),也包括交 叉项(下标≠)。 交叉项a,按下式计算 au=(a,a,)0.5(1-k,) (2-68)
2 流体的 p- 关系| V (2-62) Z cij = (Z口十 (2-63) Pcij =ZcijRTcij / V cij (2-64) =( i+ωj ) / 2 (2-65) 在近似计算 ij 可取为零,或查阅 nd Eng Chem Fundam , 1967 , 6: 492" 。当 1= ) 时,所有这些方程式都还原为纯物质的相应值;当 时,这些参数定义为虚拟参数,没有 意义。对比温度用 Tr=T 町计算 由式 (2 60) 计算鸟,然后代人式 (2-58) 求得混合物的 昆合物压缩因子用式 (2-28a) 计算 Z=l+ 旦主RT 气体混合物 算虽包含了许多步骤,但每一步都不复杂 整个计算过程可方便 编成程序 由计算机完成 【例 6 】 试求 CO (1 ) -C3 H 8 (2) 体系在 311K 和1. 50MPa 的条件 的混合物摩尔体积, 两组分的摩尔比为 : 7 0 计算所需的有关数据列表如下: 1 c ij Y Ezj / iVAI a V cij 2cij BO Bl Bij IJ l (m3 / kmoD ω'J l (m3 / kmol 11 304. 2 7.376 0.0942 0.274 0.225 -0.324 -0. 018 -0.1125 22 369.8 4. 246 O. 2030 O. 281 0.145 0. 474 -0.218 3660 12 335.4 5.470 O. 1416 O. 278 O. 185 O. 394 - 0.098 -0. 2100 由式 (2 59) .11 25) O. 3 X O. 7 X (-0 2100) X 0.3660) =一 O. 2777m3 / kmol Bp_1 j (-0. 2777 X lQ- 3)X 1. 50 X 106 Z= 1 + ::::_ = 1 + ' V . . • . : ' _i.V. , . /_: ~ i. VV. , iV = 0.161 839 RT ~, 8. 314 X 311 ZRT 0. 839 X 8. 314 X 311 ._ V= 一?一= v. vv: , ~~' ~::;' Vii = 1. 45 X 10 - 3 m3 / mol /J 1. 50 X 106 2.4.3 混合物的状态方程 混合物看做一个整体,可以通过海合规 从纯物质状态方程得 泪合物状态方程。 个纯物质状态方程可使用不同的混合规 ,一个混合规则也可用于不 同的状态方程,其优劣程 度由实际计算结果检验。 ( 1) RK型状态方程 RK 型状态方程 (van der Waals , RK , SRK , PR 方程)用于 昆合物时,下面的混合规 被推荐用来计算方程中的常数 am = .z= .z= aij (2-66) t ] bm = .z= (2-67) 是纯组分常数,没有 的交叉项 aij 既包括纯组分常数(下标 i= j) 也包括交 叉项( j) 交叉项 aij 按下式计算 αij =(αia)O.5 (1 -kij) (2-68)