2流体的pVT关系9圆 表2-2立方型方程三次展开式 摩尔体积V的三次展开式 RK方程n-gn+(品-RT-w)V-兴-0 (2140 RK方程n-r+a-bRT-v-=0 (2-15 P限方程n-(-bm+a一2T-3pv-+R+=0 (2-16) PT方程n-(g-c)n+[a-RT6+e)-2咖-心]v-中++-0 (2-17) 压缩因子Z的三次展开式 RK方程 (2-18) SRK方程 刀-元+tA-R_R2124B=0 (2-19) PR方程 2-(1-B)Z+(A-2B-3B)Z-(AB-P-B)-0 2.20y PT方程 -(1-C)Z+(A-B-C-2BC-B)Z-(AB-BC-BC)=0 (2-21) 上述方程中除RK方程A=ap/RT5外,其余 A=ap/R:T,B=bp/RT,C=cp/RT 立方型方程形式简单,方程中一般只有两个常 开始 数,且常数可用纯物质临界性质和偏心因子计算 读入wP了 表22列出了立方型方程三次展开式。在临界点 方程有三重实根,所求实根即为Ve;当T<T。, 计算a、b 压力为相应温度下的饱和蒸气压时,方程有三个实 根,最大根是气相摩尔体积VV(ZV),最小根是液 给初值。步长 相摩尔体积VL(Z心),中间的根无物理意义;其他 情况时,方程有一实根和两个虚根,其实根为液相 摩尔体积V九(Z孔)或气相摩尔体积Vv(Zv)。 在方程的应用中,准确地求取方程的体积根是 一个重要的环节。三次方程的求根方法有三次求根 公式和数值计算法两大类。图2-5给出了数值算法 之一的对分法求根的计算框图。该方法的思路是先 给定初值和步长,求出根的范围;然后逐次对分根 所在范围,直至求得方程的根。该方法计算过程稳 定,缺点是耗时稍多。另一种数值算法 -New g<0 to法可参阅与本教材配套的习题集0,使用时需 注意计算的收敛性。 若将立方型方程改写成表2-3中的形式,则有 可能仅仅通过手工计算就可求取方程的根,而不必 借助计算机,迭代步骤是: ①设初值Z(可用理想气体为初值,即取 ②将Z值代入式(2-25)计算h、方', 12-5对分法计算立方型方程体积根 ③将h、h'值代入表2-3中的状态方程计算 Z值: 陈钟秀,顾飞。化工热力学例题与习题.北京:化学工业出版社,1998
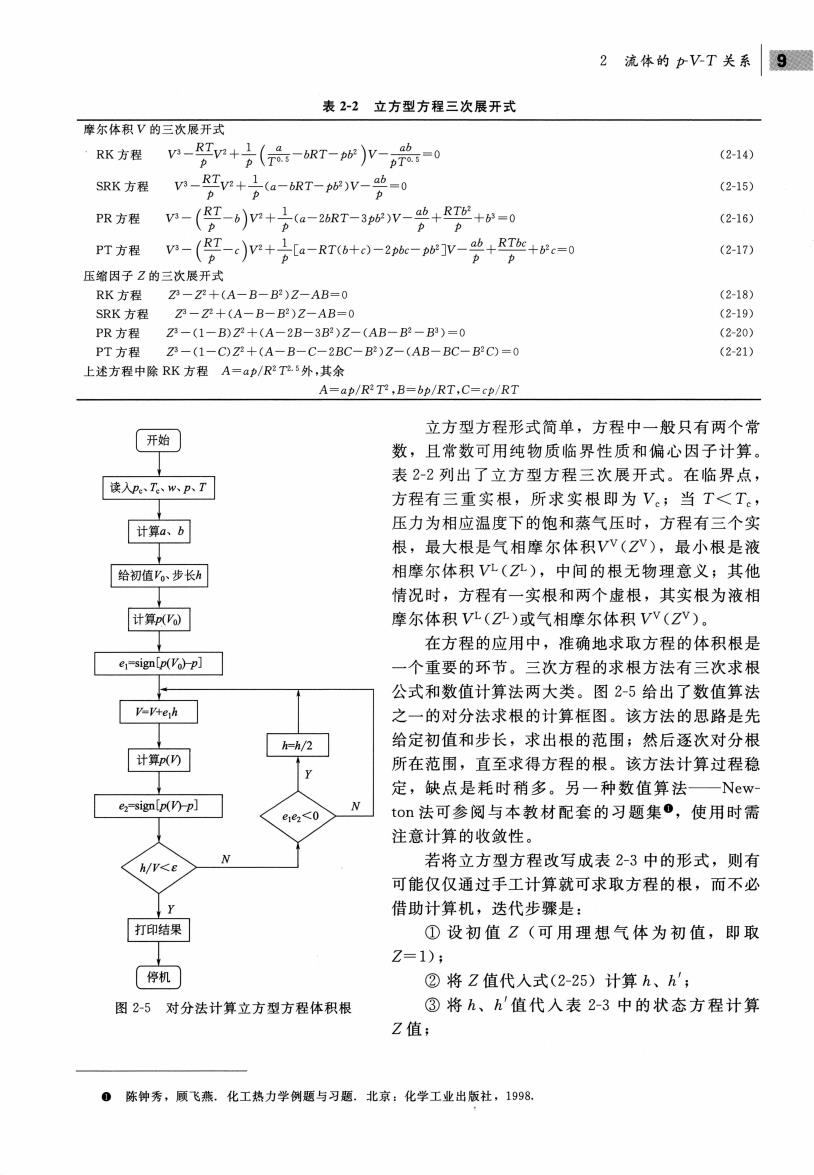
2 流体的卢 关系 2-2 立方型方程三次展开式 摩尔体积 的三次展开式 RK 方程 SRK 方程 方程 RL.o , 1 I 。飞 一一':" V'+ 一{一 -bRT-pb' 一一 p pTO.5 o RT.o , 一一':"V '-(a-bRT- pb )V一一:" 户户 IRT . \.0' 1. ~_ ~ ,", . ab , RTb' ':"-b '+ ~(a-2bRT-3pb )V- _.V + .v +b3=0 飞户 / p p (2-14 ) (2-15 ) (2-16) IRT \.0' 1 c -_. , , ~. O~ . ab , RTbc PT 方程 V3 一( "' -c RTCb+c) 2pb -pb'] 一一+b'c 飞卢 / p p ( 2-17) 压缩因子 的三次展开式 RK 方程 Z3 - Z' + (A- B - B' )Z -AB= O SRK 方程 Z3 - Z' + (A - B-B' )Z-AB= O PR 方程 (l -B)Z +(A 2B 3B )Z-(AB- B' - B3) = 0 (2-18) (2-19 ) (2-20) PT 方程 Z3- (l-C) 万十 (A-B-C-2BC-B')Z AB BC C) =O (2-21) 述方程中除 RK 方程 A=ap y2.5 外,其余 A=a R' bp RT C= RT 2-5 对分法计算立方型方程体积根 立方型方程形式简单,方程中一般只有两个常 且常数可用纯物质临界性质和偏心因子计算。 2-2 了立方型方程三次展开式。在临界点 方程有三重实根,所求实根 压力为相应温度下的饱和蒸气压时,方程有三个实 根,最大根是气相摩尔体积VV(Z勺,最小根是液 尔体和、 VL (Z ,中间的根无物理意义;其他 情况时, 程有 实根和两个虚根,其实根为液 摩尔体积 VL(ZL) 或气相摩尔体积 (Z 在方程的应用中,准确 求取方程的体积根是 一个重要的环节 。二次方程的求根方法有三次求根 公式和数值计算法两大类 给出了数值算法 的对分法求根的计算框图。该方法的思路是先 给定初值和步长,求出根的范围;然后逐次对分根 所在范围,直至求得方程的根。该方法计算过程稳 定,缺点是耗时稍多 种数值算法 ew ton 法可参阅 本教材配套的习题集 ,使用时需 计算的收敛性 若将立方型方程改写成表 中的形式, 可能仅仅通过手工计算就可求取 程的根,而不必 借助计算机,迭代步骤是: 设初值 (可用理想气体为初值,即取 Z= l) ; 值代入式 (2 计算 ; ③将 值代入表 2-3 的状态方程计算 值; @ 陈钟 ,顾飞燕.化工热力 例题与习 :化学工业出版社, 1998

10化工热力学 ④比较前后两次计算的Z值,若误差已达到允许范围,迭代结束;否则返回步骤②再行 计算 请注意,该方法不能用于液相体积根的计算。 表23立方型方程的另一形式 RK,SRK方程 2=合(年) (2-22) PR方程 z占合(+欢-不) (2-23) PT方程 2-己6合(+本-极)》 (2-24) 其中 h=名=艺,'-=号 (2-25) 常数A,B,C的定义见表2-2 【例2-1】将1kmol氮气压缩贮于容积为0.04636m3、温度为273.15K的钢瓶内。问此时 氮气的压力多大?分别用理想气体方程、RK方程和SRK方程计算。其实验值为101.33MPa。 解从附录二查得氨的临界参数为 T.=126.2K,p.=3.394MPa,w=0.040 氮气的摩尔体积为V=0.04636/1000=4.636×10-5m/m0l ①理想气体方程 p=RT/W=8.314×273.15/(4.636×10-5)=4.8987×10Pa 误差 (1.0133×108-4.8987×10)/1.0133×108=51.7% ②RK方程 将T、p,值代入式(2-7a)和式(2-7b),得 a=-0:4278X(8.342×126.22=1.558(Pa·m.Ka)/mo 3.394×105 6-0.08664×8.314X126.2=2.6802×105m/ml 3.394×10 代入式(26),得 8.314×273.15 1.5588 p=4.636-2.6806)X10-万-(273.15)05X4.636(4.636+2.6802)×10-0 =8.8307×107Pa 误差 (1.0133×108-8.8307×107)/1.0133×108=12.9% ③SRK方程 将w代入式(2-9d),得 m=0.480+1.574×0.040-0.176×(0.040)2=0.5426 T,=273.15/126.2=2.1644,代人式(2-9c),得 a(T)=[1十0.5426(1-2.16440.5)]2=0.5540 从式(2-9a)、式(2-9b),得 a=0.42748×8.314X026.22×0.5540=7.6816×10-2(Pa·m)/ml 3.394×10 6=0.08664x8,314X126.2=2.6784×10-5m/m0l 3.394×105 将上述值代入式(2-8),得 8.314×273.15 7.6816×10-2 p-4.636-2.6784x104.636X4.636+2.67840X10m=9.355X10PA
|化工热力学 ④比较前后两次计算的 值,若误差己达到允许范围,迭代结束;否则返回步骤②再行 计算 请注意,该方法不能用于液相体积根的计算。 (2-22) (2-23) (2-24) 立方型方程的另一形式 z= 击-;(击) z= 占去(日仨 ) z= 占一会 (l+h+: -hh ) h = ~_ = ~ .h'= _c_ =~ v Z " _ V Z 2-3 PT 方程 RK SRK 方程 PR 方程 其中 (2-25) 常数 的定义见表 2-2 【例 2-1 1kmol 氮气压缩贮于容积为 O. 04636m 、温度为 273.15K 的钢瓶内 问此时 氮气的压力多大?分别用理想气体方程、 RK 方程和 SRK 方程计算 其实验值为 10 1. 33MPa 从附录二查得氮的临界参数为 =126.2K =3.394MPa ω=0.040 氮气的摩尔体积为 V=O. 04636 / 1000=4. 636 X 10 - 5m3 / mol ①理想气体方程 p=RT/V=8. 314 X 273.15 / (4. 636 )=4.8987 10 Pa (1 .0133 X 108 -4.8987 X 107 误差 ) / 1. 0133 X 108 = 51. 7 % RK 方程 值代人式 (2-7a) 和式 (2 7b) ,得 0. 4278 X (8.314) 2 X 民= (1 26.2)2. 5 1. 5588(Pa. m6 • KO.5)/mo[2 3. 394 X 106 0. 08664 X 8. 314 X 126. 2 =2. 6802 X 10- 5m3 / mol 3. 394 X 106 1. 5588 5 (273.15) 0. 5 X 4. 636(4. 636 2. 6802) X 10 - 10 nU × -6 U- -p -Eu n v po hr nL =8.8307 X 107 Pa 误差 RK 方程 代入式 (2-9d) ,得 m=O. 480+ 1. 574 X O. 040 O. 176 X (0.040)2 =0.5426 =273.15 126.2=2.1644 ,代人式 (2-9c) ,得 (T)= [1 +0. 5426 (1 -2. 1644o. 5)J2=0. 5540 从式 (2-9a) 、式 (2 -9b) ,得 (8.314)2 X (1 26.2)2 α=0. 42748 X ~. ~:~ - . , • - -~ . ~/ XO. 5540=7. 6816X10- 2(Pa. m3 )/mol (1.0133 X 108 -8.8307 X 107 ) / 1. 0133 X 108 = 12.9 % 7.6816 X 10- 2 =9.3355 X 107 Pa 4.636 X (4.636+2.6784) X 10- 10 8. 314 X 126.2 ~ ^_~,_.^_,。 b=O. 08664 X ~ ~::: ~~:~: ~ = 2. 6784 X 10- 5 m3 / mol 3. 394 X 106 将上述值代入式 (2-8) ,得 ρ= _ 8.314X273.15 (4.636-2.6784) \;1

2流体的pV-T关系11 误差 (1.0133×108-9.3355×107)/1.0133×10=7.9% 上述计算表明,在高压低温下理想气体方程根本不能适用,RK方程亦有较大误差,SRK 方程的计算准确度则较好。 【例2-2】试用SRK和PR方程分别计算异丁烷在300K,3.704×105Pa时饱和蒸气的摩 尔体积。已知实验值为V=6.081×10-3m3/mol, 解由附录二查得异丁烷临界参数为 T。=408.1K,p.=3.648×109Pa,m=0.176 ①SRK方程 T=300/408.1=0.7351 m=0.480+1.574×0.176-0.176×0.1762=0.7516 a(T)=[1+0.7516(1-0.73510.5)]2=1.2259 b=0.08664×8.314X408.1-8.0582X10-5m/m0l 3.648×109 A=L657372910=a.09846 按式(2-22) z=是6-合(在6)-己h-8.256(1在6) 和式(2-25) h-号-00197 2 迭代计算。 ②PR方程 k=0.37464+1.54226×0.176-0.26992×0.1762=0.6377 a(T)=[1+0.6377(1-0.7351)0.5]2=1.1902 a=0.45727×8.3140X403.1D×1.1902=1.7175Pa·m6/m0e 3.648×10 1=7.2360×10-5m3/mol A-1.7175X3704X10-0.1023 (8.314)2×(300)2 B-=2.2360X97304X10-01075 按式(2-23) z-亡6会(1+2A-不)-己A9.5163(1+2A-不) 和式(2-25) A=9-Q01025 迭代计算
2 流体的 jrV 关系| 误差 (1. 0133 X 108 - 9. 3355 X 107 ) / 1. 0133 X 108 = 7. 9 % 上述计算表明,在高压低温下理想气体方程根本不能适用, RK 方程亦有较大误差, SRK 方程的计算准确度则较好 2-2 试用 SRK PR 方程分别计算异丁皖在 300K 3. 704 X 105 Pa 时饱和蒸气的摩 尔体积。已知实验值为 V=6.081 10 mol 由附录二查得异丁烧临界参数为 T c=408.1K , =3.648 10 Pa ω=0.176 SRK 方程 Tr =300/ 408. 1= 0. 7351 m=O. 480+ 1. 574 X O. 176-0. 176 X O. 1762=0. 7516 (T)= [1 +0. 7516 (1 -0. 7351 0.5 )J2= 1. 2259 (8. 314) 2 X (408. 1) 2 a=O. 42748 X w . V~.~.~: ~~~ . Á / X 1. 2259= 1. 6537(Pa • m6 ) / mo12 3. 648 X 106 8. 314 X 408. 1 b=O. 08664 X V~ v:~ :: ~~~~ Á =8.0582 X 10 - 5 m3 / mol 《、: 106 A=l 6537 × 3.704 × 105 ;;:-::- = O. 09846 (8.314)2 (300)2 8. 0582 X 10 - 5 X 3. 704 X 105 =0.01197 8.314 X 300 按式 (2-22) n nL -H 6 A-B h-M -H Z 和式 (2-25) nu- l-z QZ - B-z 'n 迭代计算。 PR 方程 k=O. 37464+ 1. 54226 O.176 O. 26992 X O.1762=0. 6377 (T)= [1 +0. 6377 (1 -0. 7351) 0.5 J 2= 1. 1902 (8.314) 2 X (408.1) 2 α=0. 45727 X w. V~.~ ,~:~~~~. Á/ X 1. 1902= 1. 7175Pa. m6 / moF 3. 648 X 106 8. 314 X 408. 1 b=O. 07780 ~v::::~~~~ Á 7.2360 X 10 -5 m3 / mol ‘: 106 1. 7175 X 3. 704 X 105 =0. 1023 (8.314)2 X (300)2 7.2360 X 10- 5 X 3.704 X 105 =0.01075 8. 314 X 300 按式 (2-23) Z=Tt 一会(币仨F)=Tt-95 叫百七万) 和式 (2-25) num-z - nu- - B z - 'h 迭代计算

12化工热力学 ③取初值Z=1,迭代计算结果见下表。 SRK方程 PR方程 选代次数 00110 0.01075 0.9148 0.01308 0.9107 a.01184 0.9071 0.01320 0.9019 0.01192 0.062 0.01321 0.01193 0.061 0.9012 SRK方程 V=ZRT-0.9061X8.314X300-6.1015X10-m2/ml 3.704×10 误差 (6.031-6.1015)×10-2/6.031×10-2=-1.2% PR方程 v-Z8T-0g2%8x80-665×10-m/aml P 误差 (6.031-6.0685)×10-2/6.031×10-2=-0.6% 从以上计算看出,迭代收敛速度很快,仅迭代四次即得终点。SRK和PR方程都有较好 的计算准确度,其结果均可为工程界接受。 2.2.3多常数状态方程 与简单的状态方程相比,多常数方程的优点是应用范围广,准确度高;缺点是形式复杂, 计算难度和工作量都较大。由于电子计算机的日益普及,克服这些缺点已不成问题,因此多常 数方程正越来越多地在工程计算中得到应用。 (1)Virial方程(1901年) Virial不是人名而是“力”的意思,方程提出者为Onnes,方程的形式为 z-1++号++. (2-26) 或者 Z-等=1+Bp+Cp2+Dp+. (2-27) 式中,B(B)、C(C)、D(D)、.分别称为第二、第三、第四、.Virial系数。对一 定的物质来说,这些系数仅仅是温度的函数。 Virial方程具有坚实的理论基础,其系数有着确切的物理意义,如第二Virial系数是考虑 到两个分子碰撞或相互作用导致的与理想行为的偏差,第三Virial系数则是反映三个分子碰撞 所导致的非理想行为。因为两个分子间的相互作用最普遍,而三分子相互作用、四分子相互作 用等的概率依次递减。因此方程中第二Virial系数最重要,在热力学性质计算和相平衡中都有 应用。高次项对Z的贡献逐项迅速减小,只有当压力较高时,更高的Virial系数才变得重要。 方程式(226)和式(2-27)为无穷级数,如果以舍项形式出现时,方程就成为近似式。从 工程实用上来讲,在中、低压时,取方程式(2-26)和式(2-27)的二项或三项即可得合理的近 似值。Virial方程的二项截断式如下 2-x-1+8 (2-28a) 或 Z-器=1+Bp=1+影 (2-28b) 式(2-28)可精确地表示低于临界温度、压力为1.5MPa左右的蒸气的pV-T性质。当压 力超过适用范围而在5MPa以上时,需把Virial方程舍项成三项式,方能得到满意结果,即
|化工热力学 取初值 Z=l 迭代计算结果见下表 SRK 方程 PR 方程 迭代次数 Z h Z h l 0.01197 l 0. 01075 l 0.9 148 0. 01308 0. 9107 0. 01184 2 O. 9071 0. 01320 0.9019 0. 01192 3 O. 9062 0.01321 0.9013 0. 01193 4 O. 9061 0.9012 SRK 方程 误差 ZRT 0. 9061X8. 314X30o ~ ._ O 0 ρ3 6.1015 10 /mol . 704X 10" (6.031-6.1015) X 10 - 2 / 6. 031 X 10 - 2 =一1. 2% ZRT 0. 9012X8. 314X300 PR 方程 V=~;~ =~ . ~~3~7~4'X =6.0685 X 10 mo 误差 (6.031-6. 0685) X 10- 2 / 6. 031 X 10- 2 =一 0.6% 从以上计算看出,迭代收敛速度很快,仅迭代四次即得终点 SRK PR 方程都有较好 的计算准确度,其结果均可为工程界接受 2. 2.3 多常数状态方程 与简单的状态方程相比,多常数方程的优点是应用范围广,准确度高;缺点是形式复杂, 计算难度和工作量都较大 由于电子计算机的日益普及,克服这些缺点已不成问题,因此多常 数方程正越来越多地在工程计算中得到应用 (1) Virial 方程(1901 年) Viria 不是人名而是"力"的意思,方程提出者为 Onnes 。方程的形式为 tJV ., B , C , D =ζ =1 十一十一丁十一 RT ~. V . V 2 . V 3 (2-26) 或者 主主 +B'p+C'p2+D'ρ3 十. (2-2 7) RT 式中 B(B') C(C') D(D') . 分别称为第二、第 、第四、. Virial 系数 对一 定的物质来说,这些系数仅仅是温度的函数 irial 方程具有坚实的理论基础,其系数有着确切的物理意义,如第二 Vi-r ia 系数是考虑 到两个分子碰撞或相互作用导致的与理想行为的偏差,第 Virial 系数则是反映 个分子碰撞 所导致的非理想行为 因为两个分子间的相互作用最普遍,而 分子相互作用、四分子相互作 用等的概率依次递减 因此方程中第二 Viria 系数最重要,在热力学性质计算和相平衡中都有 应用 高次项对 的贡献逐项迅速减小,只有当压力较高时,更高的 Tirial 系数才变得重要。 方程式 (2-26) 和式 (2-27) 为无穷级数,如果以舍项形式出现时,方程就成为近似式。从 工程实用 来讲,在中、低压时,取方程式 (2-26 )和式 (2-27) 的二项或三项即可得合理的近 似值 Virial 方程的二项截断式如下 B-v + P-R v-T Z (2-28a) Z= 主主 =l+B'ρ=1+ 旦主 (2-28b) RT ~. - r . RT (2 28) 可精确地表示低于临界温度、压力为1. 5MPa 左右的蒸气的户V-T 性质。当压 力超过适用范围而在 5MPa 以上时,需把 Virial 方程舍项成三项式,方能得到满意结果,即

2流体的pVT关系13 z-Y-1+B+9 (2-29) 由于对第三Virial系数以后的Virial系数知道很少,且高于三项的Virial式使用起来不方 便,所以对于更高的压力,通常都采用其他状态方程。 由统计力学可从理论上计算各项Virial系数,即 B-2NA (e-Ro-1)dr (2-30) (2-31) 式中,r(r)为两分子间的位能;r为分子中心间距离;NA为Avogadro常数;k为 Boltzmann?常数;fi=exp(-Tg/kT)-l。 对第四和更高的Virial系数也可导出类似的式子。但由于分子间相互作用十分复杂,至今 建立的分子间位能函数仅对简单分子有较好精度,大多数物质的Virial系数还需要通过实验测 定。许多气体的第二Virial系数可从文献或有关手册中查到。当查不到数据时,可用普遍化的 方法估算,这将在下一节讨论。 (2)Martin-Hou方程(1955年) 该方程1955年由Martin和侯虞钧●提出,简称MH方程。1959年Martin对该方程作了 进一步的改进,提高了其在较高密度区的精确度。1981年侯虞钩等®又将方程的适用范围扩展 到液相区。 Martin-Hou方程的通式为 (2-32) 其中f,(T)=A,+B,T+C,exp(-5.475T/T) 81型MH方程的展开式为 p-。+4+BT+C5.5T/T2+ RT (V-b)2 (2-33) 式中,A2,B,C2,A,B,C3,A4,B4,B,及b皆为方程的常数,可从纯物质临界 参数T。、p。、V。及饱和蒸气压曲线上的一点数据(TS、p)求得。 81型MH方程用于烃类和非烃类气体均令人十分满意,一般误差小于1%。对许多极性 物质如NH3、H2O在较宽的温度范围和压力范围内,都可以得到精确的结果,对量子气体 H2、H等也可应用,目前它已成功地用于合成氨的工艺计算。在汽液两相区,对比温度T 约从0.65到临界温度,对诸如二氧化碳、正丁烷、氩、甲烷及氮等各类物质,方程计算的饱 和液相摩尔体积与文献数据比较平均偏差不到5%,一般在2%~3%,同时饱和气相摩尔体积 的偏差在1%以内。 (3)Benedict-Webb-Rubin方程(1940年) 该方程属于Virial型方程,简称BWR方程,在计算和关联轻烃及其混合物的液体和气体 热力学性质时极有价值。其表达式为
川严 关系 睛里 c-mv + B-v + Ar-R v-T Z (2-29) 由于对第 Virial 系数以后的 Virial 系数知道很少,且高于三项的 Virial 式使用起来不方 便,所以对于更高的压力,通常都采用其他状态方程。 由统计力学可从理论上计算各项 Virial 系数,即 B =- 21rNA ~ (e kT (2-30) 一只1rNi rr12 C= ~. 'r. I I 1" " !lzf13 ! Z3 r1Z 13 rZ3 dr1Z dr13 drZ3 ,) J Q J Q J Ir 12- r 13 1 式中, r(γ) 为两分子间的位能 为分子中心间距离; Avogadro 常数 Boltzmann常数 !ij = exp ( - rij j k T) -1 对第四和更高的 Virial 系数也可导出类似的式子。但由于分子间相互作用十分复杂,至今 建立的分子间位能函数仅对简单分子有较好精度,大多数物质的 Viri 系数还需要通过实验测 许多气体的第二 Virial 系数可从文献或有关手册中查到 当查不到数据时,可用普遍化的 方法估算,这将在下一节讨论 (2) Martin-Hou 方程(1 955 年) 该方程 1955 年由 Martin 和侯虞钧@提出,简称 MH 方程 19 59 Martin 对该方程作了 进一步的改进,提高了其在较高密度区的精确度 19 年侯虞钧等@又将方程的适用范围扩展 到液相区 ( 2-31) Martin Hou 方程的通式为 ρ=÷fλβ(σT ;纪-写~ (V 的) , 其中 (T) =Ai + BiT+C xpμ( 一一-5. 475Tj T c ) 81 MH 方程的展开式为 RT . T + Cz exp ( - 5. 475T j T c ) V 一一一 ? - b . (V- b) Z (2-32) ( 2-33) A3+B3T+C3exp (-5. 475Tj T c ) I A4 + B4 T I B5 T (V- b)3 ' (V-b) 4 ' (V-b)5 式中,鸟,鸟, Cz ' 鸟, C3' A4' 皆为方程的常数,可从纯物质临界 参数 、矶、 及饱和蒸气压曲线上的 点数据 TS 得。 81 MH 方程用于短 和非怪类 体均 人十分满 ,一般误差小于 对许多极性 物质如 NH 在较宽的温度范围和压力范围内,都可以得到精确的结果,对量子气 陀、 He 等也可应用,目前它已成功地用于合成氨的工艺计算 在汽液两相区,对比温度 约从 O. 65 到临界温度,对诸如二氧化碳、正丁烧、 、甲皖及氮等 物质,方程计 的饱 和液相 尔体积与文献数据比较 均偏差不到 般在 %~ ,同时饱和 摩尔体积 的偏 以内 (3) dict bb Rubin (1 940 该方程属于 Virial 型方程,简称 BWR 方程,在计算和关联轻怪及其混合物的液体和气体 热力学性质时极有价值。其表达式为 o Martin J J, Hou Y C. AIChE J, 1955 , 1: 142, • 侯虞钩 ,张彬, 唐宏青. 工学报, 1981, 1: 1