
4化工热力学 1.3.5热与功 热是研究热现象中引进的概念。热力学中,热的定义是通过体系的边界,体系与体系(或 体系与环境)之间由于温差而传递的能量。需要指出: ①不能把热视为是贮存在体系内的能量,它只是能量的传递形式。当能量以热的形式传 人体系后,不是以热的形式贮存,而是增加了该体系的内能。 ②热不是状态函数,它与过程变化的途径有关。 ③习惯规定,体系吸热为正值,体系放热为负值。 功是体系与环境之间传递能量的又一种形式。热力学中定义:“功是除温差以外的其他势 差而引起体系与环境之间传递的能量。”由于做功的方式不同,存在各种形式的功,如机械功、 电功、化学功、表面功、磁功等。 在热力学中,经常遇到有限压缩过程或膨胀过程的做功方式。如果过程是可逆进行,那么 做功的表达式W=-业pdV,式中,p为体系的压力:V、V分别为过程前、后的体积值。 做功表达式中负号是为了与功所采用的习惯符号一致。功也不是状态函数,其数值与过程变化 的途径有关。习惯规定,体系对环境做功为负值,而环境对体系做功为正值
化工热力学 1. 3. 5 热与功 热是研究热现象中引进的概念 热力学中,热的定义是通过体系的边界,体系与体系(或 体系与环境)之间由于温差而传递的能量。需要指出: ①不能把热视为是贮存在体系内的能量,它只是能量的传递形式 当能量以热的形式传 入体系后,不是以热的形式贮存,而是增加了该体系的内能。 ②热不是状态函数,它与过程变化的途径有关 ③习惯规定,体系吸热为正值,体系放热为负值。 功是体系与环境之间传递能量的又一种形式。热力学中定义"功是除温差以外的其他势 差而引起体系与环境之间传递的能量。"由于做功的方式不同,存在各种形式的功,如机械功、 电功、化学功、表面功、磁功等 在热力学中,经常遇到有限压缩过程或膨胀过程的做功方式。如果过程是可逆进行,那么 rv_ 做功的表达式 w= 'pdV 式中, 为体系的压力; 分别为过程前、后的体积值。 J V, 做功表达式中负号是为了与功所采用的习惯符号一致。功也不是状态函数,其数值与过程变化 的途径有关。习惯规定,体系对环境做功为负值,而环境对体系做功为正值

2流体的DV-T关系 在众多的热力学性质中,流体的压力p、摩尔体积V和温度T是可以通过实验测量的: 利用流体pVT数据和热力学基本关系式可计算不能直接从实验测得的其他性质,如焙H、 内能U、嫡S、自由焓G等。因此,流体pVT关系的研究是一项重要的基础工作。 2.1纯物质的pV-T关系 图2-1的三维曲面显示了处于平衡态下的纯物质pVT关系,曲面以上或以下的空间是不 平衡区。三维曲面上“固”、“液”和“气(汽)”分别代表固体、液体和气体的单相区,“固 汽”、“固-液”和“液-汽”分别表示固汽、固液和液汽平衡共存的两相区。两相区在伞T图 (图22)上的投影是三条相平衡曲线,升华线、熔化线和汽化线,三线的交点是三相点。汽 化线的另一个端点是临界点C,它表示汽液两相能共存的最高压力和温度,即临界压力p。和 临界温度T。高于临界压力和温度的区域称为超临界流体区。从液体到流体或从气体到流体 固液 化 相 一升华曲线 图21纯物质的pVT图 都是渐变过程,不存在相变。超临界的流体既不同于液体,又不同于气体。它的密度可以接近 液体,但具有类似气体的体积可变性和传递性质,可作为特殊的萃取溶剂和反应介质。因此, 开发超临界流体区的分离技术和反应技术,近年来成为 引人注目的热点。 流体力VT关系,还可以用以T为参变量的力V 图表示,见图2-3。图中高于临界温度的等温线T1、 T2,曲线平滑且不与相界线相交,近于双曲线,即 固相 pV-常数。小于临界温度的等温线T、T,由三个不同 部分组成。中间水平线段表示汽液平衡共存,在给定温 三相点 度下对应一个确定不变的压力,即该纯物质的饱和蒸气 升华曲线 压。汽液平衡混合物的组成从左端100%液体变化到右 度 端100%气体。曲线AC为饱和液体线,曲线BC为饱 图22纯物质的T图
2 流体的 ]r V-T 关系 在众多的热力学性质中,流体的压力 、摩尔体积 和温度 是可以通过实验测量的; 利用流体户V-T 数据和热力学基本关系式可计算不能直接从实验测得的其他性质 如焰 内能 、情 、自由焰 因此,流体 jrV 关系的研究是一项重要的基础工作 2. 1 纯物质的 p- V-T 关系 2-1 维曲面显示了处于平衡态下的纯物质 jrV-T 关系,曲面以上或以下的空间是不 平衡区 三维曲面上"固"、"液"和"气 汽)"分别代表固体、液体和气体的单相区;"固 汽"、"固-液"和"液-汽"分别表示固汽、固液和液汽平衡共存的两相区 两相区在 jrT (图 2-2) 上的投影是三条相平衡曲线,升华线、熔化线和汽化线,三线的交点是三相点 化线的另一个端点是临界点 ,它表示汽液两相能共存的最高压力和温度,即临界压力 临界温度 高于临界压力和温度的区域称为超临界流体区 从液体到流体或从气体到流体 v 纯物质的 frV 都是渐变过程,不存在相变。超临界的流体既不同于液体,又不同于气体 它的密度可以接近 液体,但具有类似气体的体积可变性和传递性质,可作为特殊的萃取溶剂和反应介质 因此, 开发超临界流体区的分离技术和反应技术,近年来成为 引人注目的热点 流体户V-T 关系,还可以用以 为参变量的 -V 图表示,见图 2-3 图中高于临界温度的等温线 T] T2 曲线平滑且不与相界线相交,近于双曲线,即 pV= 常数 小于临界温度的等温线 由三个不同 部分组成 中间水平线段表示汽液平衡共存,在给定温 度下对应一个确定不变的压力,即该纯物质的饱和蒸气 汽液平衡混合物的组成从左端 100 液体变化到右 100 气体 曲线 AC 为饱和液体线,曲线 BC 为饱 PC 3 固相 2- A- 翩刁 B~_' 气相 -'- Tc 温度 纯物质的 frT
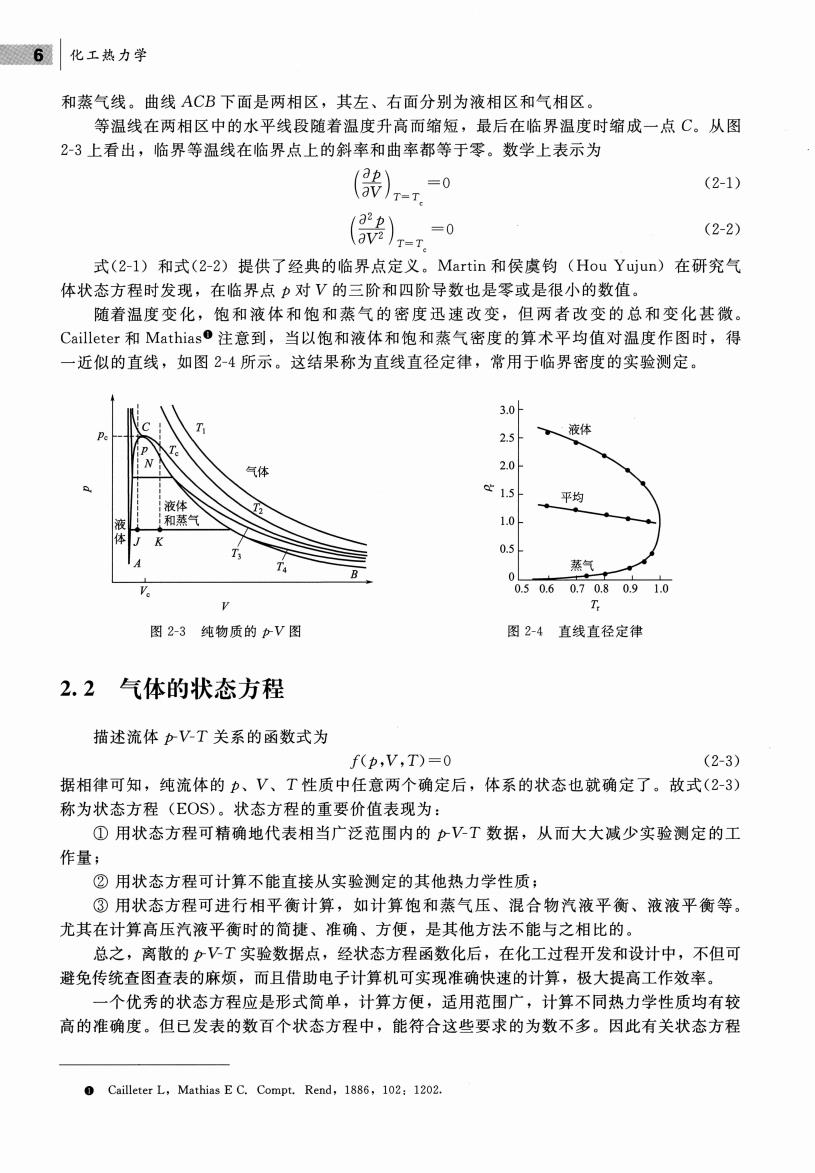
6化工热力学 和蒸气线。曲线ACB下面是两相区,其左、右面分别为液相区和气相区 等温线在两相区中的水平线段随着温度升高而缩短,最后在临界温度时缩成一点C。从图 2-3上看出,临界等温线在临界点上的斜率和曲率都等于零。数学上表示为 (影)-=0 (2-1) (2-2) 式(?-1)和式(2-2)提供了经典的临界点定义,Martin和侯虞钧(Hou Yujun)在研究气 体状态方程时发现,在临界点p对V的三阶和四阶导数也是零或是很小的数值。 随着温度变化,饱和液体和饱和蒸气的密度迅速改变,但两者改变的总和变化甚微。 Cailleter和Mathias0注意到,当以饱和液体和饱和蒸气密度的算术平均值对温度作图时,得 近似的直线,如图2-4所示。这结果称为直线直径定律,常用于临界密度的实验测定。 30叶 251 液体 20 15 平均 1.0 T 05 蒸气】 050607080910 图23纯物质的pV图 图24直线直径定律 2.2气体的状态方程 描述流体pVT关系的函数式为 f(p,V,T)=0 (2-3) 据相律可知,纯流体的p、V、T性质中任意两个确定后,体系的状态也就确定了。故式(2-3) 称为状态方程(EOS)。状态方程的重要价值表现为: ①用状态方程可精确地代表相当广泛范围内的pV-T数据,从而大大诚少实验测定的工 作量: ②用状态方程可计算不能直接从实验测定的其他热力学性质: ③用状态方程可进行相平衡计算,如计算饱和蒸气压、混合物汽液平衡、液液平衡等。 尤其在计算高压汽液平衡时的简捷、准确、方便,是其他方法不能与之相比的 总之,离散的pVT实验数据点,经状态方程函数化后,在化工过程开发和设计中,不但可 避免传统查图查表的麻烦,而且借助电子计算机可实现准确快速的计算,极大提高工作效率。 ,个优秀的状态方程应是形式简单,计算方便,适用范围广,计算不同热力学性质均有较 高的准确度。但已发表的数百个状态方程中,能符合这些要求的为数不多。因此有关状态方程 Cailleter L.Mathias EC.Compt.Rend,1886,102:1202
|化工热力学 和蒸气线。曲线 ACB 下面是两相区,其左、右面分别为液相区和气相区。 等温线在两相区中的水平线段随着温度升高而缩短,最后在临界温度时缩成一点 从图 2-3 上看出,临界等温线在临界点上的斜率和曲率都等于零 数学上表示为 (坠élV )=0 J T=T (2-1) (21 )=0 élV2 J T=T (2-2) (2- 1)和式 (2-2) 提供了经典的临界点定义 Martin 和侯虞钧 (Hou Yujun) 在研究气 体状态方程时发现,在临界点 的三阶和四阶导数也是零或是很小的数值 随着温度变化,饱和液体和饱和蒸气的密度迅速改变,但两者改变的总和变化甚徽 Cailleter Mathias 注意到,当以饱和液体和饱和蒸气密度的算术平均值对温度作图时,得 一近似的直线,如图 -4 所示。这结果称为直线直径定律,常用于临界密度的实验测定。 3.0 PC•- 2.5 2.0 1>. 巳: 1.5 1.0 0.5 0 0.5 0.6 1.0 y -3 纯物质的户 -4 直线直径定律 2.2 气体的状态方程 描述流体户V-T 关系的函数式为 f( , T)=O (2-3) 据相律可知,纯流体的 性质中任意两个确定后,体系的状态也就确定了。故式 (2-3) 称为状态方程 (EOS) 。状态方程的重要价值表现为: ①用状态方程可精确地代表相当广泛范围内的 j:r V-T 数据,从而大大减少实验测定的工 作量; ②用状态方程可计算不能直接从实验测定的其他热力学性质; 用状态方程可进行相平衡计算,如计算饱和 蒸气压、 昆合物汽液平衡、液液平衡等。 尤其在计算高压汽液平衡时的简捷、准确、方便,是其他方法不能与之相比的。 总之,离散的 j:r V-T 实验数据点,经状态方程函数化后,在化工过程开发和设计中,不但可 避免传统查图查表的麻烦,而且借助电子计算机可实现准确快速的计算,极大提高工作效率。 一个优秀的状态方程应是形式简单 ,计算方便,适用范围广,计算不同热力学性质均有较 高的准确度。但已发表的数百个状态方程中,能符合这些要求的为数不多。因此有关状态方程 o Cailleter L , Mathias E c. Compt. Rend , 1886 , 102: 1202

2流体的pV-T关系7 的深入研究尚在继续进行。 状态方程按形式、结构通常可分为两类:非解析型和解析型。解析型状态方程又分为密度 为三次方的立方型方程和多常数Virial型方程。非解析型方程主要针对特定流体作高精度描 述,无普适性。本教材介绍重要而常用的解析型状态方程。 2.2.1理想气体方程 理想气体方程是最简单的状态方程,即 pV=RT或p= (2-4) 式中,p为气体压力;V为气体摩尔体积;T为绝对温度;R为通用气体常数,其数值见 表21。 表21通用气体常数R的值 R 甲 位 1.987卡/(摩尔·K) calo/(mol·K) 83.14k厘米2·巴)/(摩尔 K (emr·barP)/(mad·K 8.314焦耳/(摩尔·K 1/(ol,K3 8.31 82.05(厘米大气压)/(摩尔0(cmatm2)/(mlK) ×103 =10Pa. 理想气体是极低压力和较高温度下各种真实气体的极限情况,实际上并不存在。理想 气体方程除了在工程设计中可用作近似估算外,更重要的是为判断真实气体状态方程的正 确程度提供了一个标准。当p→0或者V○时,任何真实气体状态方程都应还原为理想气 体方程。 使用状态方程时,应注意通用气体常数R的单位必须和p、V、T的单位相适应。 2.2.2立方型状态方程 所谓立方型状态方程是因为方程可展开为体积(或密度)的三次多项式。van der Waals 方程(1873年)是第一个适用真实气体的立方型方程,是对理想气体方程(24)的校正。 RT (2-5) 方程中常数a、b分别是考虑到分子有体积和分子间存在相互作用的校正。利用临界点(3p aV)=0,(3p/V2)=0的条件可确定 Q= 64P。 虽然van der Waals方程准确度不高,无很大实用价值,但建立方程的理论和方法对以后 立方型方程的发展产生了重大影响。目前工程上广泛采用的立方型方程基本上都是从van der Waals方程衍生出来的。其中有代表性的有如下几个。 (1)Ridlich-Kwang方程(1949年) Ridlich-Kwang方程简称RK方程,其形式为 RT P-V-bTO.SV(V+b (2-6) 式中,a、b是方程常数,与流体的特性有关,由纯物质临界性质计算 a=0.42748R2T.5/p. (2-7a) b=0.08664RT./p. (2-7b) RK方程适用非极性和弱极性化合物,计算准确度比van der Waals方程有很大提高,但
2 流体的 p- 关系| 的深入研究尚在继续进行 状态方程按形式、结构通常可分为两类:非解析型和解析型 解析型状态方程又分为密度 为三次方的立方型方程和多常数 Virial 型方程 非解析型方程主要针对特定流体作高精度描 述,无普适性。本教材介绍重要而常用的解析型状态方程 2.2.1 理想气体方程 理想气体方程是最简单的状态方程,即 RT pV=RT ρ=~:; (2-4) V 式中, 为气体压力 ;V 为气体摩尔体积 ;T 为绝对温度 ;R 为通用气体常数,其数值见 2-1 R 1. 987 /( 摩尔 K) 141 焦耳/( 摩尔 K) 82 05 厘米 大气压) (摩尔.K ( 1cal=4.1861. ( 1atm= 1. 013 X 105 Pa , ( 1bar= 2-1 通用气体常数 的值 R | 单位 cal( /(mol . K) 83. 14 1( 厘米 (摩尔. K) (cm3 • bar<3l )/(mol. K) .082051( 气压) (千摩尔. K) (m' . atm)/ (laml. K) (米 中自 )/( 千摩尔 K) (m3 • Pa)/ (kmol • K) J/(mol. K) (cm3 'atm(%) )/ (mol.K) 理想气体是极低压力和较高温度下各种真实气体的极限情况,实际上并不存在 理想 气体方程除了在工程设计中可用作近似估算外,更重要的是为判断真实气体状态方程的正 确程度提供了 个标准 或者 时,任何真实气体状态方程都应还原为理想气 体方程 使用状态方程时,应注意通用气体常数 的单位必须和户、 的单位相适应 2.2.2 立方型状态方程 所谓立方型状态方程是因为方程可展开为体积(或密度)的三次多项式 van der Waals 方程(1 873 年)是第一个适用真实气体的立方型方程,是对理想气体方程 (2-4) 的校正 ρ= 卫王丘 V-b V 2 (2-5) 方程中常数 分别是考虑到分子有体积和分子间存在相互作用的校正 利用临界点 (òp òV)=O , (ò ÒV2) =0 的条件可确定 27R2 ~ RT a=6 7;b-8P 虽然 van der Waals 方程准确度不高,无很大实用价值,但建立方程的理论和方法对以后 立方型方程的发展产生了重大影响。目前工程上广泛采用的立方型方程基本上都是从 van der Waals 方程衍生出来的 其中有代表性的有如下几个 (1) Ridlich-Kwang 方程(1949 年) Ridlich-K wang 方程简称 RK 方程,其形式为 RT a P=V-b - TO. 5V(V+b) (2-6) 式中, 是方程常数,与流体的特性有关,由纯物质临界性质计算 a=0.42748R :5/ c (2-7a) b=0.08664RTc/ pc (2-7b) RK 方程适用非极性和弱极性化合物,计算准确度比 van der Waals 方程有很大提高,但

8化工热力学 对多数强极性化合物仍有较大偏差。 (2)Soave-Ridlich-Kwang方程(1972年) p-v (Ty (2-8) 方程简称SRK方程。Soave对RK方程的改进是将原方程中的常数a作为温度函 数,即 a(T)=ae×a(T)=0.42748R2T/p.×a(T) (2-9a) b=0.08664RT./p. (2-9b) a(T)=[1+m(1-T5)]2 (2-9c) m=0.480+1.574w-0.176w2 (2-9d) 式中,仙为偏心因子 SK方程提高了对极性物质和量子化流体pV-T计算的准确度。更主要的是Soave对方 程的改进使方程可用于饱和液体密度的计算。在此基础上,用单一的SRK方程便可较精确地 计算汽液平衡,拓宽了方程应用的领域, (3)Peng-Robinson方程(1976年) V(V+8FV-D) (TY (2-10) 其中 a(T)=aeXa(T)=0.45724R2T8/p.×a(T) (2-11a) b=0.07780RT:/p (2-11b) a(T)=1+k(1-0.5)2 (2-11c) k=0.3746+1.54226m-0.269922 (2-11d) Peng-Robinson(PR)方程中常数a仍是温度的函数,对体积表达的更精细的修正目的 是为了提高方程计算Z。和液体密度的准确性。因此P℉方程在计算饱和蒸气压、饱和液相 密度方面有更好的准确度。PR方程和SRK方程一样,是工程相平衡计算中最常用的方程 之一。 (4)Patel-Teja方程(1982年) (2-12) 其中 a(T)=Q,R2T/p.Xa(T) (2-13a) b-QuRT:/p. (2-13b) c=nRT。/p (2-13c) a(T)=[1+F(1-T9.5)]2 (2-13d) 2a、2和n。的计算方法如下 n。=1-3 0,=3g+3(1-2)2,+0%+n 而,是下式中最小的正根 +(2-3)2+3n-=0 上述诸式中的点及F是两个经验参数,由纯物质的饱和性质求得。 Patel-Teia(PT)方程中引进了新的常数c,常数个数达到三个。常数多有利于提高方程 的准确度,但也给方程的简明性和易算性带来损失。用PT方程计算了一些极性和非极性纯物 质的饱和气体和液体密度,其平均偏差分别为1.44%和2.94%(1070个数据点)。用PT方程 计算轻烃、醇水等体系的汽液平衡也取得较好结果
!化工热力学 对多数强极性化合物仍有较大偏差。 (2) Soave-Ridlich Kwang 方程(1 972 年) PRTG(T) (2-8) V-b V(V+b) 该方程简称 SRK 方程。 Soave RK 方程的改进是将原方程中的常数 作为温度函 数,即 a(T)= Xα( T)=0.42748R f/ (T) b=0.08664RT c α( T) = [1 + m ( 1 - 1';. 5 ) J2 m =O. 480+ 1. 574ωO. 176w2 式中, 为偏心因子。 (2-9a) (2-9b) (2-9c) (2-9d) SRK 方程提高了对极性物质和量子化流体户V-T 计算的准确度 。更 主要的是 Soave 对方 程的改进使方程可用于饱和液体密度的计算 。在此基础上,用单一的 SRK 方程便可较精确地 计算汽液平衡,拓宽了方程应用的领域。 其中 (3) Peng-Robinson 方程(1 976 年) ρRT -G T) V-b V(V+ b)+b(V-b) a(T) =ac α(T)=0.45724R :/ (T) b=0.07780RT ρc (2-10) (2-11a) (2-11 b) (T) = [1 +k(1-1';. 5) J2 (2-11c) k=O. 3746+ 1. 54226ω O. 26992w2 (2-11d) Peng-Robinson (PR) 方程中常数 仍是温度的函数,对体积表达的更精细的修正目的 是为了提高方程计算 和液体密度的准确性 因此 PR 方程在计算饱和蒸气压、饱和液相 密度方面有更好的准确度 PR 方程和 SRK 方程一样,是工程相平衡计算中最常用的方程 之一 (4) Patel-Teja 方程(1 982 年) 其中 .a .a 的计算方法如下 而且是下式中最小的正根 = RT a(T) V-b V(V+ b) +c(V-b) (T)= 2 ~/ c (T) b= bRTc c c= cRTc C a( T) =[1 + F(1- 1';.5 )J2 =1-3.;c .aa =3 +3 (1 -2';c) .a +.a~ +.ac +(2-3.;c)ο~ +3fc .a =0 上述诸式中的 '; 是两个经验参数,由纯物质的饱和性质求得。 (2-12) (2-13a) (2-13b) (2-13c) (2-13d) Patel-Teja (PT) 方程中引进了新的常数 常数个数达到 常数多有利于提高方程 的准确度,但也给方程的简明性和易算性带来损失。用 PT 方程计算了一些极性和非极性纯物 质的饱和气体和液体密度,其平均偏差分别为1. 44% 2.94% (1 070 个数据点) PT 方程 计算轻短、醇水等体系的汽液平衡也取得较好结果