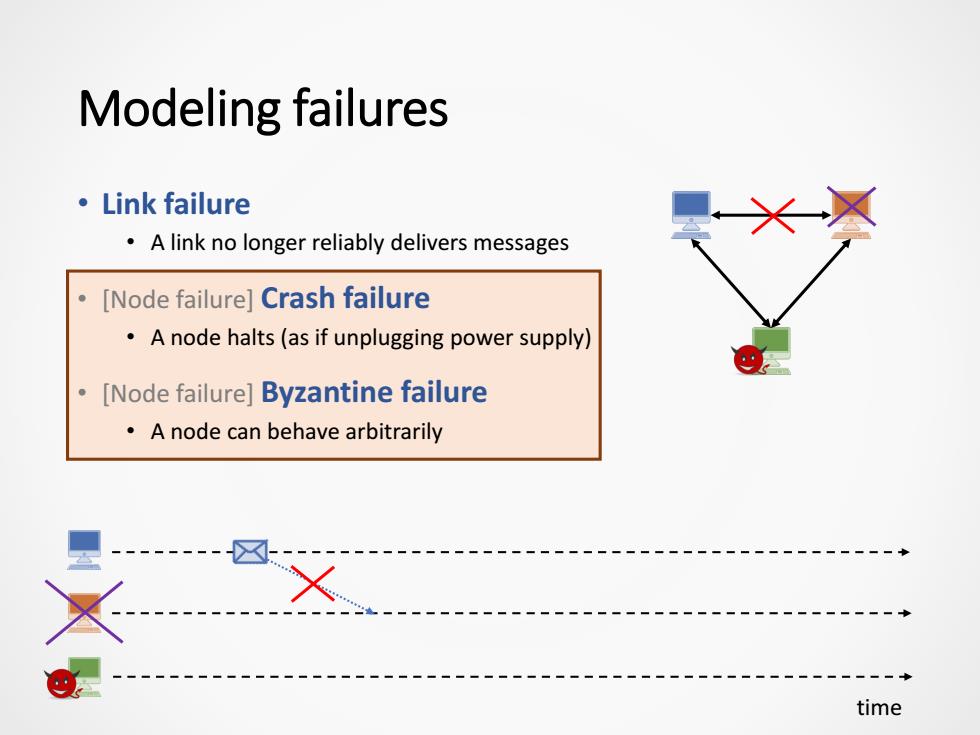
Modeling failures 。Link failure A link no longer reliably delivers messages [Node failure]Crash failure A node halts(as if unplugging power supply) [Node failure]Byzantine failure A node can behave arbitrarily ------- time
Modeling failures • Link failure • A link no longer reliably delivers messages • [Node failure] Crash failure • A node halts (as if unplugging power supply) • [Node failure] Byzantine failure • A node can behave arbitrarily time
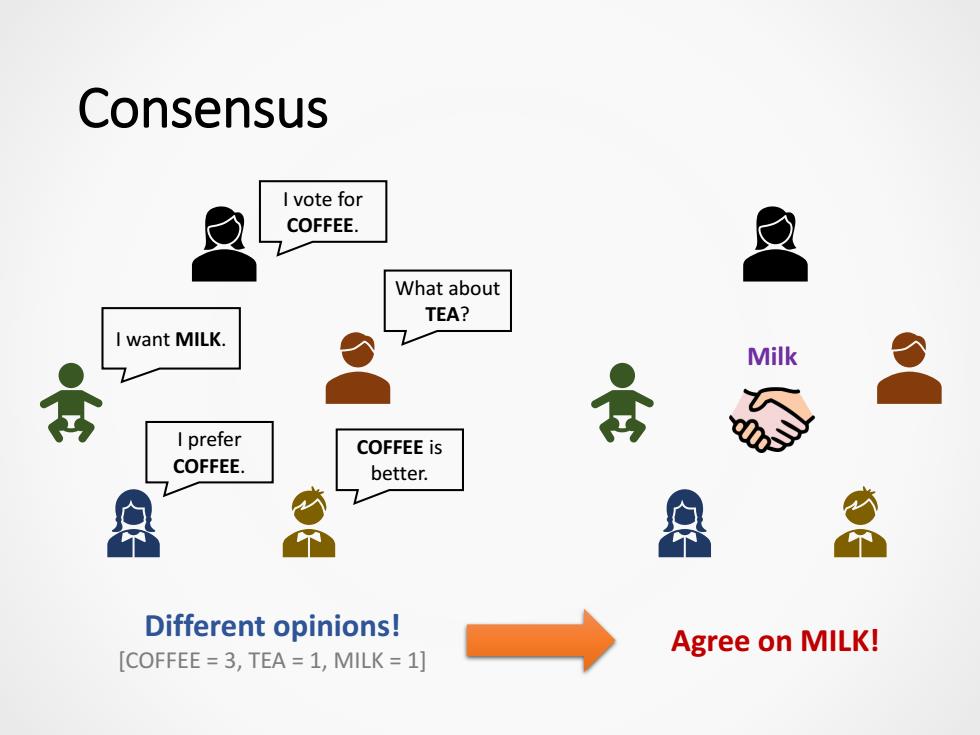
Consensus I vote for COFFEE. What about TEA? I want MILK. Milk I prefer COFFEE is COFFEE. better. Different opinions! Agree on MILK! [COFFEE=3,TEA=1,MILK =1]
Consensus COFFEE is better. What about TEA? I vote for COFFEE. I prefer COFFEE. I want MILK. Milk Different opinions! [COFFEE = 3, TEA = 1, MILK = 1] Agree on MILK!

Consensus ·A set of n nodes{1,2,…,n} Input of node i:some value vi Output of node i:some value outi Requirement:all nodes have identical output value. Termination:each node eventually outputs some value. Agreement:all nodes output identical value Validity:final output value is some node's initial value Applications in distributed computing: 北京 Electing a leader among nodes Replicating data into nodes Taking a commit decision 成都 上海
Consensus • A set of 𝑛 nodes 1,2, ⋯ , 𝑛 Input of node 𝑖: some value 𝑣𝑖 Output of node 𝑖: some value 𝑜𝑢𝑡𝑖 Requirement: all nodes have identical output value. • Termination: each node eventually outputs some value. Agreement: all nodes output identical value. Validity: final output value is some node’s initial value. 北京 成都 上海 Applications in distributed computing: • Electing a leader among nodes • Replicating data into nodes • Taking a commit decision • …

Consensus ·A set of n nodes{1,2,…,n Input of node i:some value vi Output of node i:some value outi Requirement:all nodes have identical output value. Termination:each node eventually outputs some value. Agreement:all nodes output identical value. Validity:final output value is some node's initial value. 北京 In this talk,we assume: Network graph is a complete graph ·Each initial value vi∈{0,1} 成都 上海
Consensus • A set of 𝑛 nodes 1,2, ⋯ , 𝑛 Input of node 𝑖: some value 𝑣𝑖 Output of node 𝑖: some value 𝑜𝑢𝑡𝑖 Requirement: all nodes have identical output value. • Termination: each node eventually outputs some value. Agreement: all nodes output identical value. Validity: final output value is some node’s initial value. • In this talk, we assume: • Network graph is a complete graph • Each initial value 𝑣𝑖 ∈ 0,1 北京 成都 上海

Distributed Consensus in Synchronous Systems [with crash failure tolerance]
Distributed Consensus in Synchronous Systems [with crash failure tolerance]