
Cluster expansion lemma 中科院计算所量子计算与算法理论实验室 何昆 hekun@ict.ac.cn https://theory.ict.ac.cn/cn/ https://theory.ict.ac.cn/en/members/hekun/
中科院计算所 量子计算与算法理论实验室 何 昆 hekun@ict.ac.cn Cluster expansion lemma https://theory.ict.ac.cn/en/members/hekun/ https://theory.ict.ac.cn/cn/

m bad event:A{A1,A2,...,Am} Lovasz Local Lemma (asymmetric version): 3a:A→[0,1) A∈A:Pr[A≤aAnI(1-aa) →公 II(1-@a) A∈A BEr(A) neighborhood:r(A)[BEA I A and B are adjacent in the dependency graph} Example: A2 A1(X1,X4) A A4(X4) A3 A2(X1,X2) A5 A5(X3) A4 A3(X2,X3) dependency graph X1,X2,X3,X4 (max degree d) are mutually independent
m bad event: 𝒜 ≜ {𝐴1, 𝐴2, … , 𝐴𝑚} 𝐴1(𝑋1, 𝑋4) 𝐴2(𝑋1, 𝑋2) 𝐴3(𝑋2, 𝑋3) 𝐴4(𝑋4) 𝐴5(𝑋3) 𝑋1, 𝑋2, 𝑋3, 𝑋4 are mutually independent dependency graph Example: (max degree d) Lovász Local Lemma (asymmetric version): ∀𝐴 ∈ 𝒜: Pr[𝐴] ≤ 𝛼𝐴 ∏ 𝐵∈Γ(𝐴) (1 − 𝛼𝐵) ∃𝛼: 𝒜 → [0,1) Pr ሥ 𝑖=1 𝑚 𝐴𝑖 > ∏ 𝐴∈𝒜 (1 − 𝛼𝐴) neighborhood: Γ(𝐴) ≜ {𝐵 ∈ 𝒜 ∣ 𝐴 and 𝐵 are adjacent in the dependency graph}
Lovasz Local Lemma (asymmetric version): 3:A→[0,1) HA∈A:Pr[A]≤aAI(1-aB) (1-A) AEA BEr(A) VA∈凡:A=1-aA A HA CLA三1+LA 1 (1-B)= 1十HA BETCA) 1+B =LA BEr(A) BEr+(A 1+B HA HA IIBEr+(A)(1+B)EIsr+(A)IIBEI B Example: 。+(A)={A1=A,A2} ·ΠBer+A(1+B)=1·1+A1·1+1·A2+A1·A2 inclusive neighborhood: T+(A)会T(A)U{A
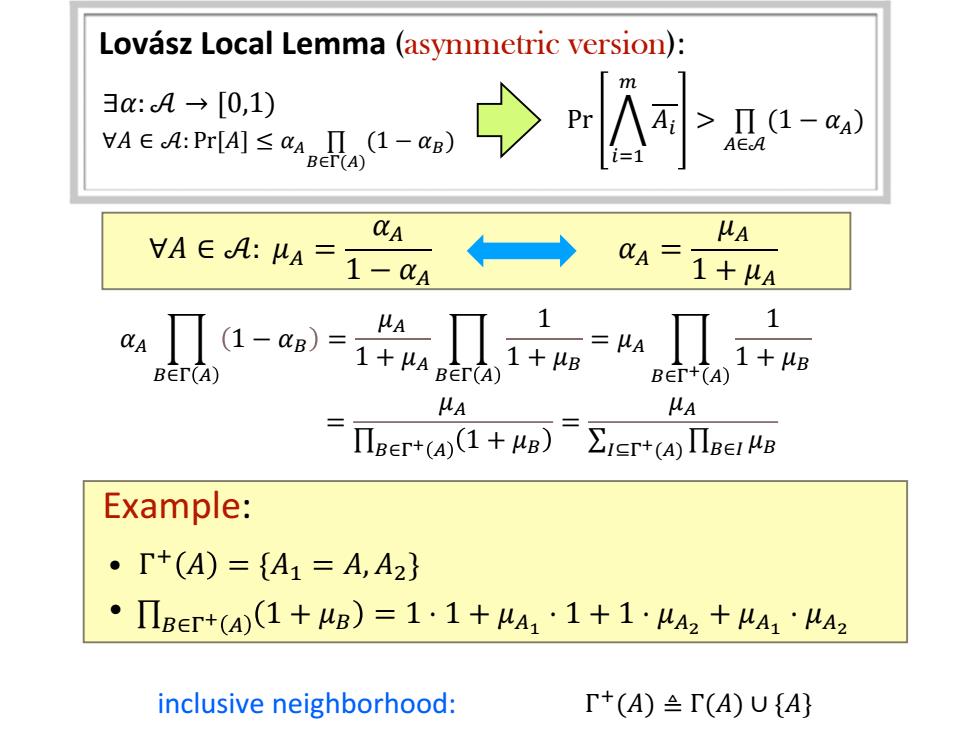
Lovász Local Lemma (asymmetric version): ∀𝐴 ∈ 𝒜: Pr[𝐴] ≤ 𝛼𝐴 ∏ 𝐵∈Γ(𝐴) (1 − 𝛼𝐵) ∃𝛼: 𝒜 → [0,1) Pr ሥ 𝑖=1 𝑚 𝐴𝑖 > ∏ 𝐴∈𝒜 (1 − 𝛼𝐴) ∀𝐴 ∈ 𝒜: 𝜇𝐴 = 𝛼𝐴 1 − 𝛼𝐴 𝛼𝐴 = 𝜇𝐴 1 + 𝜇𝐴 𝛼𝐴 ෑ 𝐵∈Γ 𝐴 1 − 𝛼𝐵 = 𝜇𝐴 1 + 𝜇𝐴 ෑ 𝐵∈Γ 𝐴 1 1 + 𝜇𝐵 = 𝜇𝐴 ෑ 𝐵∈Γ+ 𝐴 1 1 + 𝜇𝐵 = 𝜇𝐴 ∏𝐵∈Γ+ 𝐴 1 + 𝜇𝐵 = 𝜇𝐴 σ𝐼⊆Γ+(𝐴) ∏𝐵∈𝐼 𝜇𝐵 Γ + inclusive neighborhood: (𝐴) ≜ Γ(𝐴) ∪ {𝐴} • Γ + 𝐴 = {𝐴1 = 𝐴, 𝐴2} • ∏𝐵∈Γ+ 𝐴 1 + 𝜇𝐵 = 1 ⋅ 1 + 𝜇𝐴1 ⋅ 1 + 1 ⋅ 𝜇𝐴2 + 𝜇𝐴1 ⋅ 𝜇𝐴2 Example:

Lovasz Local Lemma (asymmetric version): m 3a:A→[0,1) AeA:Pr[A≤aAIa-g) BET(A) 思- VA∈L:a=1-aA A MA A= 1+uA A1-ae=1+ar LA一 1 BEr(A) 1+B =WA 1+B BEr+(A) HA HA TIBEr+(A(1+B)EIsr+(A)IIBeUB Lovasz Local Lemma (asymmetric version): 3:A→(0,+∞) AetPiWsZerileae inclusive neighborhood: +(A)会T(A)U{A
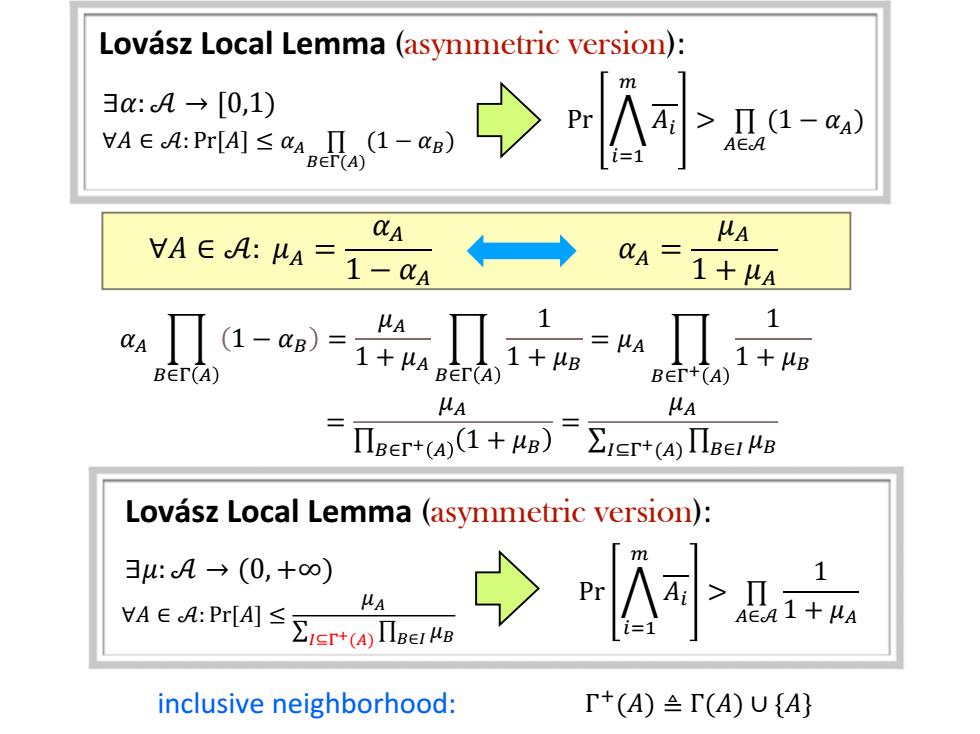
Lovász Local Lemma (asymmetric version): ∀𝐴 ∈ 𝒜: Pr[𝐴] ≤ 𝛼𝐴 ∏ 𝐵∈Γ(𝐴) (1 − 𝛼𝐵) ∃𝛼: 𝒜 → [0,1) Pr ሥ 𝑖=1 𝑚 𝐴𝑖 > ∏ 𝐴∈𝒜 (1 − 𝛼𝐴) ∀𝐴 ∈ 𝒜: 𝜇𝐴 = 𝛼𝐴 1 − 𝛼𝐴 𝛼𝐴 = 𝜇𝐴 1 + 𝜇𝐴 𝛼𝐴 ෑ 𝐵∈Γ 𝐴 1 − 𝛼𝐵 = 𝜇𝐴 1 + 𝜇𝐴 ෑ 𝐵∈Γ 𝐴 1 1 + 𝜇𝐵 = 𝜇𝐴 ෑ 𝐵∈Γ+ 𝐴 1 1 + 𝜇𝐵 = 𝜇𝐴 ∏𝐵∈Γ+ 𝐴 1 + 𝜇𝐵 = 𝜇𝐴 σ𝐼⊆Γ+(𝐴) ∏𝐵∈𝐼 𝜇𝐵 Lovász Local Lemma (asymmetric version): ∀𝐴 ∈ 𝒜: Pr[𝐴] ≤ 𝜇𝐴 σ𝐼⊆Γ+(𝐴) ∏𝐵∈𝐼 𝜇𝐵 ∃𝜇: 𝒜 → (0, +∞) Pr ሥ 𝑖=1 𝑚 𝐴𝑖 > ∏ 𝐴∈𝒜 1 1 + 𝜇𝐴 Γ + inclusive neighborhood: (𝐴) ≜ Γ(𝐴) ∪ {𝐴}
Lovasz Local Lemma (asymmetric version): m 3:A→[0,1) HA∈A:Pr[A]≤aAI(1-aB) AEA】 BEr(A) VA∈凡:A=1-aA XA HA CLA三1十LA 1 1 (1-aB)= 1十HA BET(A) 1+B =LA BEr(A) BEr+(A) 1+B HA HA ΠBer+A(1+4B) EIsr+(A TIBEI HB Lovasz Local Lemma (asymmetric version): 3:A→(0,+∞) VA内s2iee A inclusive neighborhood: T+(A)兰T(A)U{A
Lovász Local Lemma (asymmetric version): ∀𝐴 ∈ 𝒜: Pr[𝐴] ≤ 𝛼𝐴 ∏ 𝐵∈Γ(𝐴) (1 − 𝛼𝐵) ∃𝛼: 𝒜 → [0,1) Pr ሥ 𝑖=1 𝑚 𝐴𝑖 > ∏ 𝐴∈𝒜 (1 − 𝛼𝐴) ∀𝐴 ∈ 𝒜: 𝜇𝐴 = 𝛼𝐴 1 − 𝛼𝐴 𝛼𝐴 = 𝜇𝐴 1 + 𝜇𝐴 𝛼𝐴 ෑ 𝐵∈Γ 𝐴 1 − 𝛼𝐵 = 𝜇𝐴 1 + 𝜇𝐴 ෑ 𝐵∈Γ 𝐴 1 1 + 𝜇𝐵 = 𝜇𝐴 ෑ 𝐵∈Γ+ 𝐴 1 1 + 𝜇𝐵 = 𝜇𝐴 ∏𝐵∈Γ+ 𝐴 1 + 𝜇𝐵 = 𝜇𝐴 σ𝐼⊆Γ+(𝐴) ∏𝐵∈𝐼 𝜇𝐵 Lovász Local Lemma (asymmetric version): ∀𝐴 ∈ 𝒜: Pr[𝐴] ≤ 𝜇𝐴 σ𝐼⊆Γ+(𝐴) ∏𝐵∈𝐼 𝜇𝐵 ∃𝜇: 𝒜 → (0, +∞) Pr ሥ 𝑖=1 𝑚 𝐴𝑖 > ∏ 𝐴∈𝒜 1 1 + 𝜇𝐴 Γ + inclusive neighborhood: (𝐴) ≜ Γ(𝐴) ∪ {𝐴}