
?.竖向地震作用的计算范围和计算方法: 8.结构地震反应的时程分析法的概念,适用范围: 9.结构抗震承载力的验算和结构抗震变形的验算。 五、主要知识点补充解释 1.单自由度弹性体系的地震反应分析 (1)单自由度弹性体系在地震作用下的运动方程 m元(t)十c文(t)十kx(t)=一mx,() 还可简化为: 十25wt+uw2x=-元 式中 仙=√k/m -2wum -2 J/km (2)自由振动 自由振动方程:五+2Xw文十w2x=0 自振周期: T=2x/w 体系的频率: f=11T 体系的圆频率。 0=2r/T=2可 单自由度体系自振周期的计算公式:T=2π√m/k 自振周期是结构的一种固有属性,也是结构本身一个很重要的动力特性 (3)强迫振动 杜哈默积分: ()-d()(e-tu-"sinw (-r)dr (4)运动方程的通解 ()()co)(sina!t(e-ina (t-)dr
7.竖向地震作用的计算范围和计算方法; 8.结构地震反应的时程分析法的概念,适用范围; 9.结构抗震承载力的验算和结构抗震变形的验算。 五、主要知识点补充解释 1.单自由度弹性体系的地震反应分析 (1)单自由度弹性体系在地震作用下的运动方程 还可简化为: 式中 (2)自由振动 自由振动方程: 自振周期: 体系的频率: 体系的圆频率: 单自由度体系自振周期的计算公式: 自振周期是结构的一种固有属性,也是结构本身一个很重要的动力特性。 (3)强迫振动 杜哈默积分: (4)运动方程的通解

2.单自由度弹性体系的水平地展作用及其反应谱 (1)计算水平地震作用的基本公式 P=s=网高ce ①地震系数:表示地面运动的最大加速度与重力加速度之比。 k=运l g 一般地,地面运动加速度愈大,则地震烈度愈高,故地震系数与地震烈度之间存在着 定的对应关系。 ②动力系数B: B =Tto lma S。 它是单质点最大绝对加速度与地面最大加速度的比值,表示由于动力效应,质点的最大 绝对加速度比地面最大加速度放大了多少倍。 (2)标准反应谱 由于地震的随机性,即使在同一地点、同一烈度,每次地震的地面加速度记录也很不一 致,因此需要根据大量的强震记录计算出对应于每一条强震记录的反应谱曲线,然后统计求 出最有代表性的平均曲线作为设计依据,这种曲线称为标准反应谱曲线, 根据不同地面运动记录的统计分析可以看出,场地土的特性、震级以及震中距等都对反 应谱曲线有比较明显的影响。 (3)设计反应谱 为了便于计算,《抗震规范》采用相对于重力加速度的单质点绝对最大加速度,即α 与体系自振周期T之间的关系作为设计用反应谱。 地震影响系数a: a=S./g=k8 则: F=aG ▣实际上就是作用于单质点弹性体系上的水平地震力与结构重力之比
2.单自由度弹性体系的水平地震作用及其反应谱 (1)计算水平地震作用的基本公式 ① 地震系数:表示地面运动的最大加速度与重力加速度之比。 一般地,地面运动加速度愈大,则地震烈度愈高,故地震系数与地震烈度之间存在着一 定的对应关系。 ② 动力系数 β: 它是单质点最大绝对加速度与地面最大加速度的比值,表示由于动力效应,质点的最大 绝对加速度比地面最大加速度放大了多少倍。 (2)标准反应谱 由于地震的随机性,即使在同一地点、同一烈度,每次地震的地面加速度记录也很不一 致,因此需要根据大量的强震记录计算出对应于每一条强震记录的反应谱曲线,然后统计求 出最有代表性的平均曲线作为设计依据,这种曲线称为标准反应谱曲线。 根据不同地面运动记录的统计分析可以看出,场地土的特性、震级以及震中距等都对反 应谱曲线有比较明显的影响。 (3)设计反应谱 为了便于计算,《抗震规范》采用相对于重力加速度的单质点绝对最大加速度,即 α 与体系自振周期T之间的关系作为设计用反应谱。 地震影响系数 α: 则: α 实际上就是作用于单质点弹性体系上的水平地震力与结构重力之比
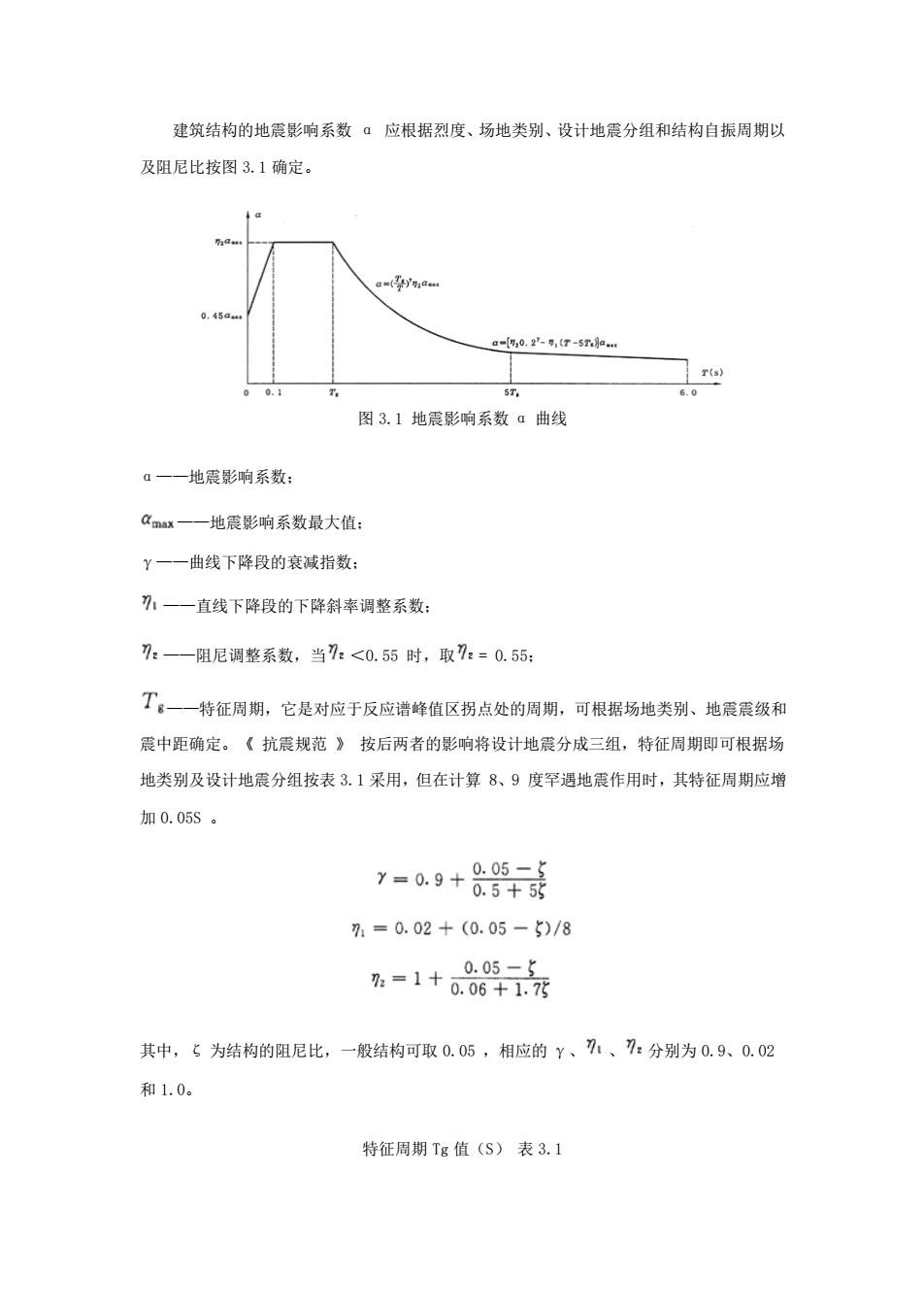
建筑结构的地震影响系数ā应根据烈度、场地类别、设计地震分组和结构自振周期以 及阻尼比按图3.1确定。 a-,0.2-5,(T-5n和: 图31地震影响系数a曲线 a一一地震影响系数: Qmax一一地震影响系数最大值: Y一一曲线下降段的衰减指数: 刀:一一直线下降段的下降斜率调整系数: 刀:一一阻尼调整系数,当7:<0.55时,取7:=0.55: T,一一特征周期,它是对应于反应谱蜂值区拐点处的周期,可根据场地类别、地震震级和 震中距确定。《抗震规范》按后两者的影响将设计地震分成三组,特征周期即可根据场 地类别及设计地震分组按表3.1采用,但在计算8、9度罕遇地震作用时,其特征周期应增 加0.05S。 7-09+885减 7=0.02+(0.05-5)/8 0.05-1 %=1+0.06+1元 其中,5为结构的阻尼比,一般结构可取0.05,相应的Y、刀:、7:分别为0.9、0.02 和1.0。 特征周期Tg值(S)表3.1
建筑结构的地震影响系数 α 应根据烈度、场地类别、设计地震分组和结构自振周期以 及阻尼比按图 3.1 确定。 图 3.1 地震影响系数 α 曲线 α——地震影响系数; ——地震影响系数最大值; γ——曲线下降段的衰减指数; ——直线下降段的下降斜率调整系数; ——阻尼调整系数,当 <0.55 时,取 = 0.55; ——特征周期,它是对应于反应谱峰值区拐点处的周期,可根据场地类别、地震震级和 震中距确定。《 抗震规范 》 按后两者的影响将设计地震分成三组,特征周期即可根据场 地类别及设计地震分组按表 3.1 采用,但在计算 8、9 度罕遇地震作用时,其特征周期应增 加 0.05S 。 其中,ζ 为结构的阻尼比,一般结构可取 0.05 ,相应的 γ、 、 分别为 0.9、0.02 和 1.0。 特征周期 Tg 值(S) 表 3.1
场地类别 第一组 0.25 0.35 0.45 0.65 第二组 0.30 0.40 0.55 0.75 第三组 0.35 0.45 0.65 0.90 水平地震影响系数最大值表3.2 烈度 地震影响 6 7 8 9 多遇地震 0.04 0.08(0.12) 0.16(0.24) 0.32 罕遇地震 0.50(0.72) 0.90(1.20) 1.40 3.多自由度弹性体系地展反应分析的振型分解法 (1)计算简图 按质量集中法将1和1+1层之间的结构重力荷载和楼面活荷载集中于楼面标高处,由无 重量的弹性直杆支撑于地面上,这样就将多层或高层结构简化为了多质点弹性体系。 m m ●m ●m 图3.2多质点体系 对于一个多质点体系,当体系只有单向振动时,则有多少个质点就有多少个自由度。 (2)运动方程 用矩阵形式表示:
场地类别 Ⅰ Ⅱ Ⅲ Ⅳ 第一组 0.25 0.35 0.45 0.65 第二组 0.30 0.40 0.55 0.75 第三组 0.35 0.45 0.65 0.90 水平地震影响系数最大值 表 3.2 地震影响 烈 度 6 7 8 9 多遇地震 0.04 0.08(0.12) 0.16(0.24) 0.32 罕遇地震 - 0.50(0.72) 0.90(1.20) 1.40 3. 多自由度弹性体系地震反应分析的振型分解法 (1)计算简图 按质量集中法将 i 和 i+1 层之间的结构重力荷载和楼面活荷载集中于楼面标高处,由无 重量的弹性直杆支撑于地面上,这样就将多层或高层结构简化为了多质点弹性体系。 图 3.2 多质点体系 对于一个多质点体系,当体系只有单向振动时,则有多少个质点就有多少个自由度。 (2)运动方程 用矩阵形式表示:

[m]z)+[c]{z+[k]{x=-[m]1} 式中的各项为: m [m]= m: . 儿kka.kn 对于上述运动方程,一般常采用振型分解法求解,而用振型分解法求解时需要利用多自 由度弹性体系的振型,它们是由分析体系的自由振动得来的。为此,需先讨论多自由度体系 的自由振动问愿。 (3)自由振动 若略去阻尼的影响,则可得自由振动方程:【m]}+]y}=和} 写成矩阵形式:(k]一w[m]){X)=0 ①自振频率: 为使其有非零解,其系数行列式必须为零,得频率方程为: 1[k]-w2[m]1=0 ②主振型 一般地,体系有多少个自由度就有多少个频率,相应的就有多少个主振型,它们是体系 的固有特性。由于某一主振型在振动过程中各质点的位移保持一定比值,且得知各质点的速 度也保持此同一比值,因此,只有各质点初始位移的比值和初速度的比值与该主振型的这些 比值相同时,也就是在这个初始条件下,才能出现这种振动的振动形式。 在一般的初始条件下,体系的振动曲线将包含全部振型。 在一般初始条件下,任一质点的振动都是由各主振型的简谐振动叠加而成的复合振动
式中的各项为: 对于上述运动方程,一般常采用振型分解法求解,而用振型分解法求解时需要利用多自 由度弹性体系的振型,它们是由分析体系的自由振动得来的。为此,需先讨论多自由度体系 的自由振动问题。 (3)自由振动 若略去阻尼的影响,则可得自由振动方程: 写成矩阵形式: ① 自振频率: 为使其有非零解,其系数行列式必须为零,得频率方程为: ② 主振型 一般地,体系有多少个自由度就有多少个频率,相应的就有多少个主振型,它们是体系 的固有特性。由于某一主振型在振动过程中各质点的位移保持一定比值,且得知各质点的速 度也保持此同一比值,因此,只有各质点初始位移的比值和初速度的比值与该主振型的这些 比值相同时,也就是在这个初始条件下,才能出现这种振动的振动形式。 在一般的初始条件下,体系的振动曲线将包含全部振型。 在一般初始条件下,任一质点的振动都是由各主振型的简谐振动叠加而成的复合振动