
●基尔霍夫边界条件 21 ∑1上波前函数为0,对场,点无贡献;∑2上的波前对场,点贡献为0;只 有光孔面∑0的波前对场,点有贡献。 ED=元∬5cos8+cos0B0as

。基尔霍夫边界条件的假设并不严格。比如,光屏面上光场为0,而 进入光孔就有了光场,这是无法满足电磁场边值关系的。但采用基 尔霍夫边界条件求解r>入区域的衍射场,还是行之有效的。 。更常见的情况是在傍轴条件求解衍射场,此时 (cos+cs) Ep=J∬Eo( 称为傍轴衍射积分式。 。由衍射积分式知,若有效波前上E0(Q)已知,则衍射场各,点E(P)确 定→整个衍射场确定!

4.1.5、衍射系统的分类 。衍射系统及其分类 (Xo,Vo) 二 ·在无成像的衍射系统中,通常按光源、衍射屏、接收屏之间距离远 近将衍射系统分为两类: 。菲涅耳衍射(近场衍射):距离均为有限远或至少其中之一为有限远 。夫琅和费衍射(远场衍射):距离均为无穷远 ●对于夫琅禾费衍射,照明光波和衍射光波均可看成平面波 ●对菲涅尔衍射,考虑两个距离都是有限远,为球面波
4.1.5、衍射系统的分类 对于夫琅禾费衍射,照明光波和衍射光波均可看成平面波 对菲涅尔衍射,考虑两个距离都是有限远,为球面波
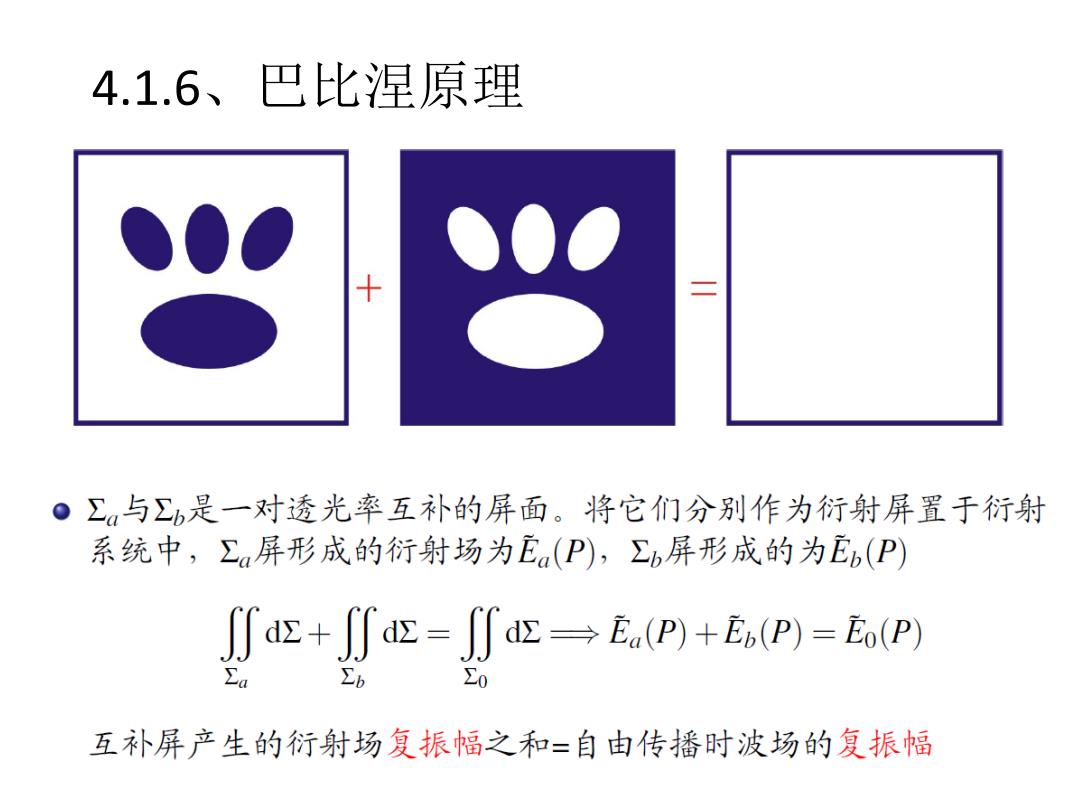
4.1.6、巴比涅原理 十 三 ·∑与∑b是一对透光率互补的屏面。将它们分别作为衍射屏置于衍射 系统中,∑a屏形成的衍射场为E(P),∑b屏形成的为Eb(P) ∬d+厂ds=∬a→E(P)+E(P)=Eo(P) ∑b 0 互补屏产生的衍射场复振幅之和=自由传播时波场的复振幅
4.1.6、巴比涅原理
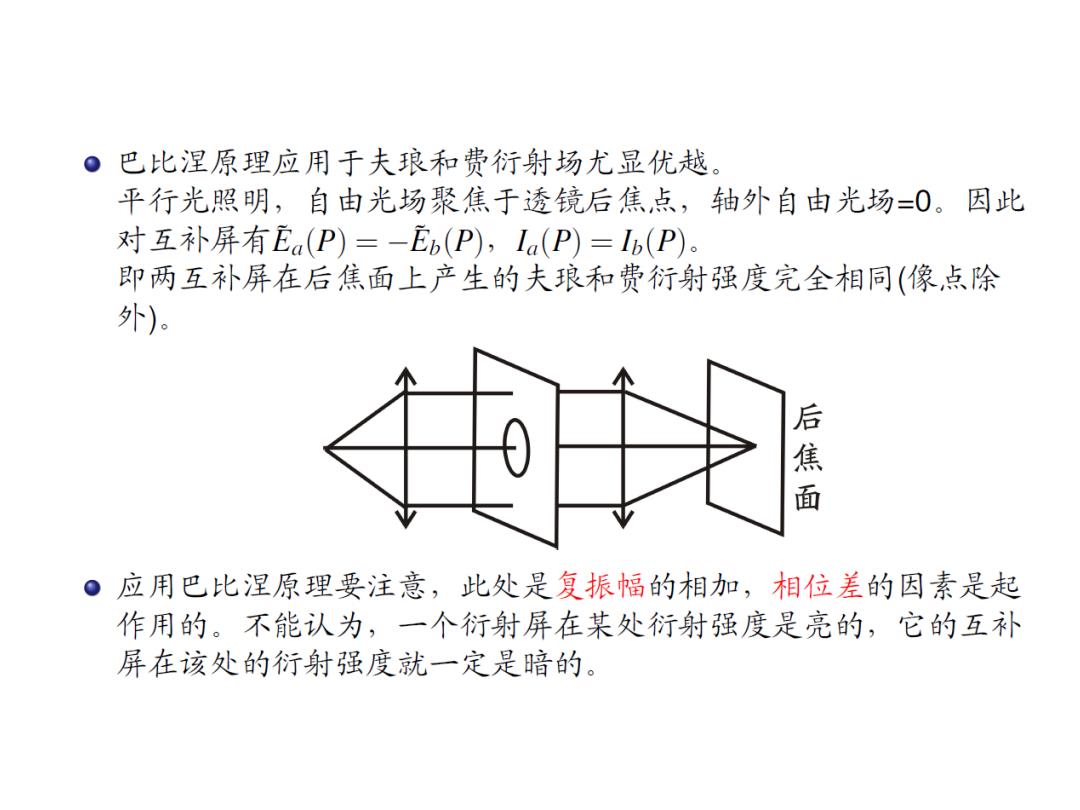
。巴比涅原理应用于夫琅和费衍射场尤显优越。 平行光照明,自由光场聚焦于透镜后焦点,轴外自由光场=0。因此 对互补屏有Ea(P)=-Eb(P),Ia(P)=lb(P)。 即两互补屏在后焦面上产生的夫琅和费衍射强度完全相同(像,点除 外)。 后 焦 。应用巴比涅原理要注意,此处是复振幅的相加,相位差的因素是起 作用的。不能认为,一个衍射屏在某处衍射强度是亮的,它的互补 屏在该处的衍射强度就一定是暗的