
第二章量子力学初步 2.1不确定关系 2.2 Schrodinger方程 2.3力学量的算符表示 2.4一维定态问题
第二章 量子力学初步 2.1 不确定关系 2.2 Schrödinger方程 2.3 力学量的算符表示 2.4 一维定态问题

量子论的实验依据 寻找以太的 热辐射的 零结果 紫外灾难 物理世界上空的两朵乌云 Lord Kelvin (William Thomson,1824~1907) 。 经典物理无法解释的实验现象 一、黑体辐射的规律、以太 。 二、光电效应
量子论的实验依据 • 经典物理无法解释的实验现象 • 一、黑体辐射的规律、以太 • 二、光电效应 热辐射的 紫外灾难 物理世界上空的两朵乌云 Lord Kelvin(William Thomson,1824~1907)

量子论的实验依据 ·黑体辐射 ·1.辐射场及其物理参数 ·2.热辐射 ·3.黑体辐射的实验规律
量子论的实验依据 • 黑体辐射 • 1.辐射场及其物理参数 • 2.热辐射 • 3.黑体辐射的实验规律
量子论的实验依据 1.黑体辐射 ·紫外灾难与系统误差 1e-23 Rayleigh-Jeans 短波段,瑞利一金斯公 Wien 10-24 Planck 式严重偏离实验结果 1e-25 。 看起来维恩的结果与实 10-26 验偏差不大,但这是 1e-27 种系统偏差,所拟合出 10-28 的公式完全不同 1a-29 10-30 10+08 1e+09 Frequency [Hz]
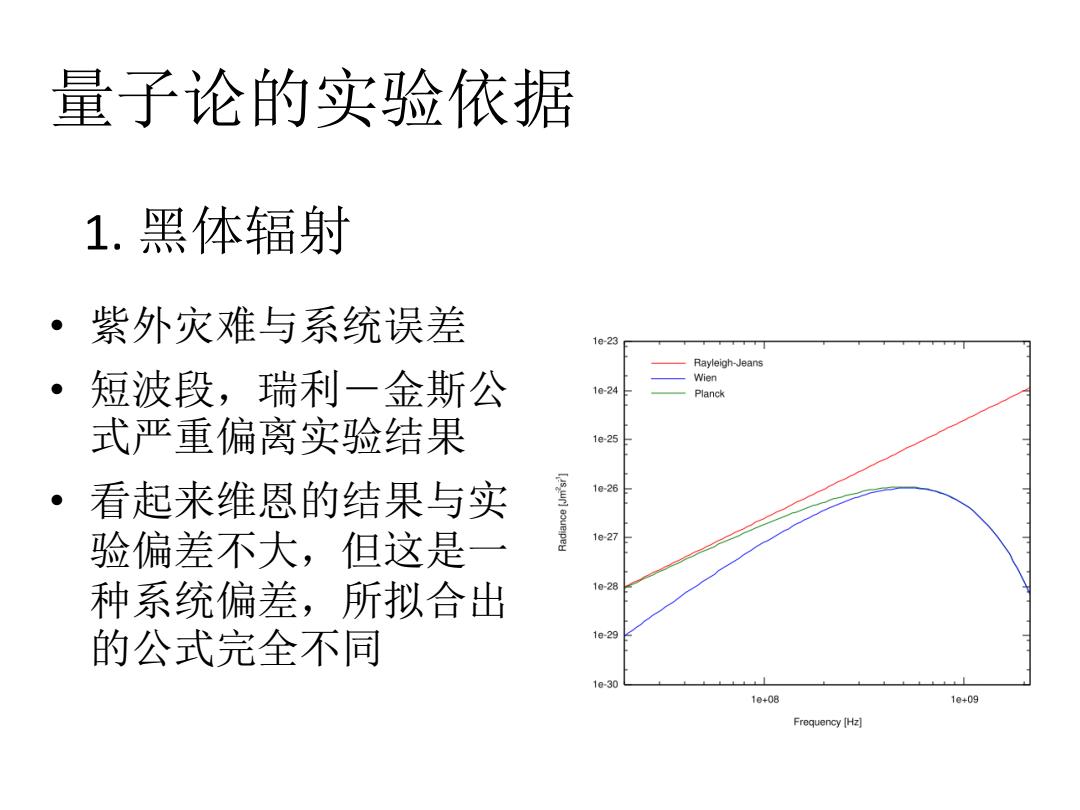
1. 黑体辐射 • 紫外灾难与系统误差 • 短波段,瑞利-金斯公 式严重偏离实验结果 • 看起来维恩的结果与实 验偏差不大,但这是一 种系统偏差,所拟合出 的公式完全不同 量子论的实验依据

能量子假说 普朗克对黑体辐射的解释 ·1900年提出,1918年获Nobel奖 空腔中的驻波是一系列的谐振子,只能取一 些分立的能量,即6=0,80,260,360,480… 8o =hv h=6.63×10-34J5 380 ◆则一个谐振子处于 nEo 能态Em=ne的几率为 e kT 260 ◆一个谐振子的平均能量为 601 n0 0 =∑neeI∑e
能量子假说 普朗克对黑体辐射的解释 • 1900年提出,1918年获Nobel奖 • 空腔中的驻波是一系列的谐振子,只能取一 些分立的能量,即 0, 0 ,2 0 ,3 0 ,4 0 0 h h Js 34 6.63 10 0 e n kT 则一个谐振子处于 能态En=nε0的几率为 0 0 2 0 3 0 一个谐振子的平均能量为 0 0 0 e / e n n kT kT n n n