
Unsupervised Hashing Iterative Quantization(ITQ)(Gong and Lazebnik,2011) max tr(WTXXTW) subject to:WTW =I It is just PCA.If W is a solution,then W =WR is also a solution where R is an orthogonal rotation matrix. Let V=XW denote the projected data,and B denote the binary code. ITQ tries to minimize the following objective function: Q(B,R)=B-VRI Learn by iterating the following two steps: o Fix R and update B:B=sign(VR); Fix B and update R:first compute the SVD of BTV as SOST,then let R=SST.It is the classic orthogonal Procrustes problem. Li (http://cs.nju.edu.cn/luj) Learning to Hash C5.NJU31/210
Unsupervised Hashing Iterative Quantization (ITQ) (Gong and Lazebnik, 2011) max tr(WT XXTW) subject to : WTW = I It is just PCA. If W is a solution, then W˜ = W R is also a solution where R is an orthogonal rotation matrix. Let V = XW denote the projected data, and B denote the binary code. ITQ tries to minimize the following objective function: Q(B, R) = ||B − V R|| Learn by iterating the following two steps: Fix R and update B: B = sign(V R); Fix B and update R: first compute the SVD of BT V as SΩSˆT , then let R = SSˆ T . It is the classic orthogonal Procrustes problem. Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS, NJU 31 / 210
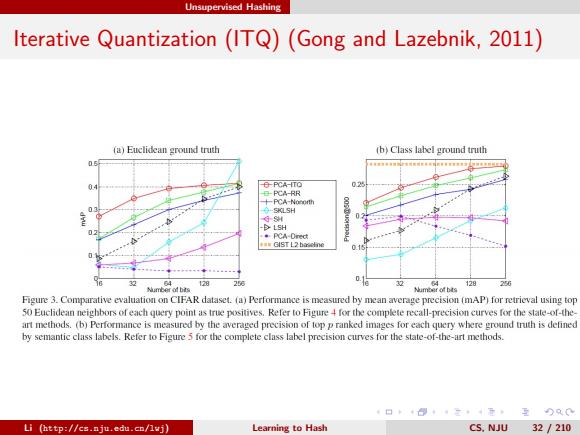
Unsupervised Hashing Iterative Quantization (ITQ)(Gong and Lazebnik,2011) (a)Euclidean ground truth (b)Class label ground truth -PCA-ITO 025 PCA-RR 十PCA-Nororth 分-5a5H 02 LSH *PCA-Drect 4■GIST L2 64 28 26 01e 32 128.250 Nuamber of bits 山nber of bts Figure 3.Comparative evaluation on CIFAR dataset.(a)Performance is measured by mean average precision (mAP)for retrieval using top 50 Euclidean neighbors of each query point as true positives.Refer to Figure 4 for the complete recall-precision curves for the state-of-the- art methods.(b)Performance is measured by the averaged precision of top p ranked images for each query where ground truth is detined by semantic class labels.Refer to Figure 5 for the complete class label precision curves for the state-of-the-art methods. 4日卡·三4元至)及0 Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS.NJU 32/210
Unsupervised Hashing Iterative Quantization (ITQ) (Gong and Lazebnik, 2011) Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS, NJU 32 / 210
Unsupervised Hashing Isotropic Hashing (IsoHash)(Kong and Li,2012b) Problem: All existing methods use the same number of bits for different projected dimensions with different variances. PCA2 PCAI Possible Solutions: o Different number of bits for different dimensions (Variable bit quantization (Moran et al.,2013)) Isotropic (equal)variances for all dimensions:Isotropic hashing (IsoHash)(Kong and Li,2012b) 重)Q0 Li (http://cs.nju.edu.cn/lvj) Learning to Hash CS.NJU 33/210
Unsupervised Hashing Isotropic Hashing (IsoHash) (Kong and Li, 2012b) Problem: All existing methods use the same number of bits for different projected dimensions with different variances. Possible Solutions: Different number of bits for different dimensions (Variable bit quantization (Moran et al., 2013)) Isotropic (equal) variances for all dimensions: Isotropic hashing (IsoHash) (Kong and Li, 2012b) Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS, NJU 33 / 210

Unsupervised Hashing Isotropic Hashing(IsoHash)(Kong and Li,2012b) To generate a code of m bits,PCA hashing (PCAH)performs PCA on X, and then use the top m eigenvectors of the matrix XXT as columns of the projection matrix WERdxm.Here,top m eigenvectors are those corresponding to the m largest eigenvalues{generally arranged with the non-increasing order X1≥A2≥·≥入m.Let 入=[A1,A2,…,AmT.Then A=WTXXTW diag(A) Define hash function h(x)=sgn(WTx) 日卡三4元,互Q0 Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS.NJU 34 /210
Unsupervised Hashing Isotropic Hashing (IsoHash) (Kong and Li, 2012b) To generate a code of m bits, PCA hashing (PCAH) performs PCA on X, and then use the top m eigenvectors of the matrix XXT as columns of the projection matrix W ∈ R d×m. Here, top m eigenvectors are those corresponding to the m largest eigenvalues {λk} m k=1, generally arranged with the non-increasing order λ1 ≥ λ2 ≥ · · · ≥ λm. Let λ = [λ1, λ2, · · · , λm] T . Then Λ = WT XXTW = diag(λ) Define hash function h(x) = sgn(WT x) Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS, NJU 34 / 210

Unsupervised Hashing Isotropic Hashing (IsoHash)(Kong and Li,2012b) Weakness of PCA Hash: Using the same number of bits for different projected dimensions is unreasonable because larger-variance dimensions will carry more information. Solve it by making variances equal (isotropic)! 日卡三4元,互Q0 Li (http://cs.nju.edu.cn/lvj) Learning to Hash C5.NJU35/210
Unsupervised Hashing Isotropic Hashing (IsoHash) (Kong and Li, 2012b) Weakness of PCA Hash: Using the same number of bits for different projected dimensions is unreasonable because larger-variance dimensions will carry more information. Solve it by making variances equal (isotropic)! Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS, NJU 35 / 210