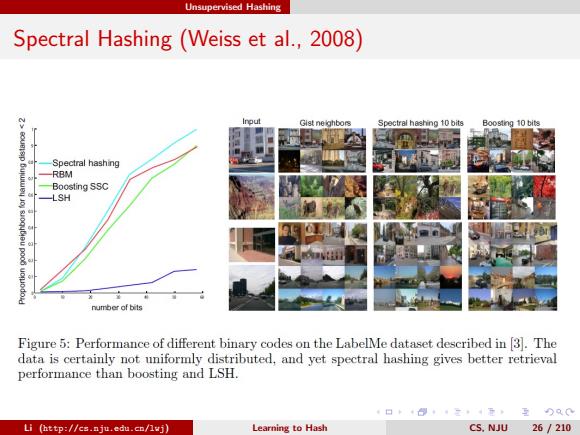
Unsupervised Hashing Spectral Hashing (Weiss et al.,2008) Gist neighbors Spectral hashing 10 bits Boosting 10 bits Spectral hashing RBM Boosting SSC -LSH number of bits Figure 5:Performance of different binary codes on the LabelMe dataset described in 3.The data is certainly not uniformly distributed,and yet spectral hashing gives better retrieval performance than boosting and LSH. ,日卡4,。二,4元,五)Q0 Li (http://cs.nju.edu.cn/lvj) Learning to Hash CS.NJU 26/210
Unsupervised Hashing Spectral Hashing (Weiss et al., 2008) Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS, NJU 26 / 210

Unsupervised Hashing Anchor Graph Hashing (AGH)(Liu et al.,2011) m吃∑Ig-P4,=t7 subject to:Ye{1,-1]nxr,1TY =0,YTY nlrxr where Aij is the similarity between points i and j. The same objective function as that in SH. Problem:the time complexity of direct eigen-decomposition is O(n3) Solution:K-means clustering to obtain m(m <n)cluster centers (anchors)u={ujER)1 Z= ∑e<ep-Dx,4yp7, j∈<i> 0,otherwise where<i>[1:m]denotes the s(s<<m)nearest anchors of xi. Li (http://cs.nju.edu.cn/lvj) Learning to Hash CS.NJU 27 /210
Unsupervised Hashing Anchor Graph Hashing (AGH) (Liu et al., 2011) min 1 2 X ij ||Yi − Yj ||2Aij = tr(Y TLY ) subject to : Y ∈ {1, −1} n×r , 1 T Y = 0, Y T Y = nIr×r where Aij is the similarity between points i and j. The same objective function as that in SH. Problem: the time complexity of direct eigen-decomposition is O(n 3 ). Solution: K-means clustering to obtain m(m << n) cluster centers (anchors) U = {uj ∈ R d} m j=1 Zij = exp(−D2 P (xi,uj )/t) j 0∈<i> exp(−D2(xi,uj 0 )/t) , ∀j ∈< i > 0, otherwise where < i >⊂ [1 : m] denotes the s(s << m) nearest anchors of xi . Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS, NJU 27 / 210

Unsupervised Hashing Anchor Graph Hashing (AGH)(Liu et al.,2011) Anchor graph:A=ZAZT where A=diag(ZT1). The solution is the r graph Laplacian eigenvectors associated with the smallest eigenvalues,which are also eigenvectors of A associated with the r largest eigenvalues(ignoring eigenvalue 1). Y=√nZA-1/2V∑-1/2=ZW where V and are the eigenvectors and eigenvalues of the small m x m matrix A-1/2ZTA-1/2. The hash function:h(x)=sign(WTz(x)) Time complexity:Decrease from O(n3)to O(nm2). Li (http://cs.nju.edu.cn/lvj) Learning to Hash CS.NJU 28 /210
Unsupervised Hashing Anchor Graph Hashing (AGH) (Liu et al., 2011) Anchor graph: Aˆ = ZΛZ T where Λ = diag(Z T 1). The solution is the r graph Laplacian eigenvectors associated with the smallest eigenvalues, which are also eigenvectors of Aˆ associated with the r largest eigenvalues (ignoring eigenvalue 1). Y = √ nZΛ −1/2V Σ −1/2 = ZW where V and Σ are the eigenvectors and eigenvalues of the small m × m matrix Λ −1/2Z TΛ −1/2 . The hash function: h(x) = sign(WT z(x)) Time complexity: Decrease from O(n 3 ) to O(nm2 ). Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS, NJU 28 / 210

Unsupervised Hashing Anchor Graph Hashing (AGH)(Liu et al.,2011) Hierarchical quantization: threshold h(x)=sgn(y) x=sgny-6 x)=sgn(-y*b】 0 -b (a)The first-ayer hashing (b)The second-layer hashing Figure 1.Hierarchical hashing on a data graph.1,...,x8 are data points and y is a graph Laplacian eigenvector. The data points of filled circles take '1'hash bit and the others take -1'hash bit.The entries with dark color in y are positive and the others are negative.(a)The first-layer hash function h'uses threshold 0;(b)the second-layer hash functions h2 use thresholds b+and b. Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS.NJU 29 /210
Unsupervised Hashing Anchor Graph Hashing (AGH) (Liu et al., 2011) Hierarchical quantization: Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS, NJU 29 / 210
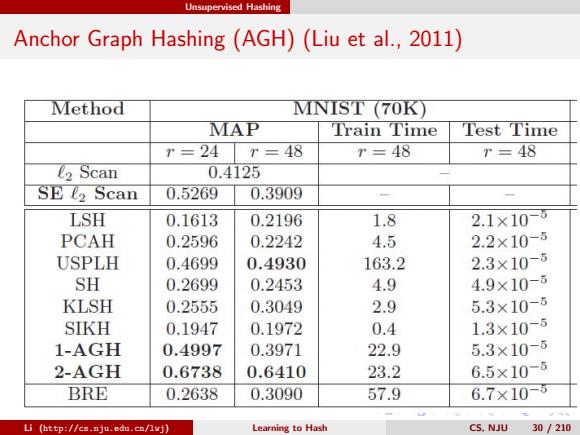
Unsupervised Hashing Anchor Graph Hashing (AGH)(Liu et al.,2011) Method MNIST (70K) MAP Train Time Test Time r=24 r=48 r=48 T=48 C2 Scan 0.4125 SE 2 Scan 0.5269 0.3909 LSH 0.1613 0.2196 1.8 2.1×10-5 PCAH 0.2596 0.2242 4.5 2.2×10-5 USPLH 0.4699 0.4930 163.2 2.3×10-5 SH 0.2699 0.2453 4.9 4.9×10-5 KLSH 0.2555 0.3049 2.9 5.3×10-5 SIKH 0.1947 0.1972 0.4 1.3×10-5 1-AGH 0.4997 0.3971 22.9 5.3×10-5 2-AGH 0.6738 0.6410 23.2 6.5×10-5 BRE 0.2638 0.3090 57.9 6.7×10-5 Li (http://cs.nju.edu.cn/lvj) Learning to Hash CS.NJU 30/210
Unsupervised Hashing Anchor Graph Hashing (AGH) (Liu et al., 2011) Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS, NJU 30 / 210