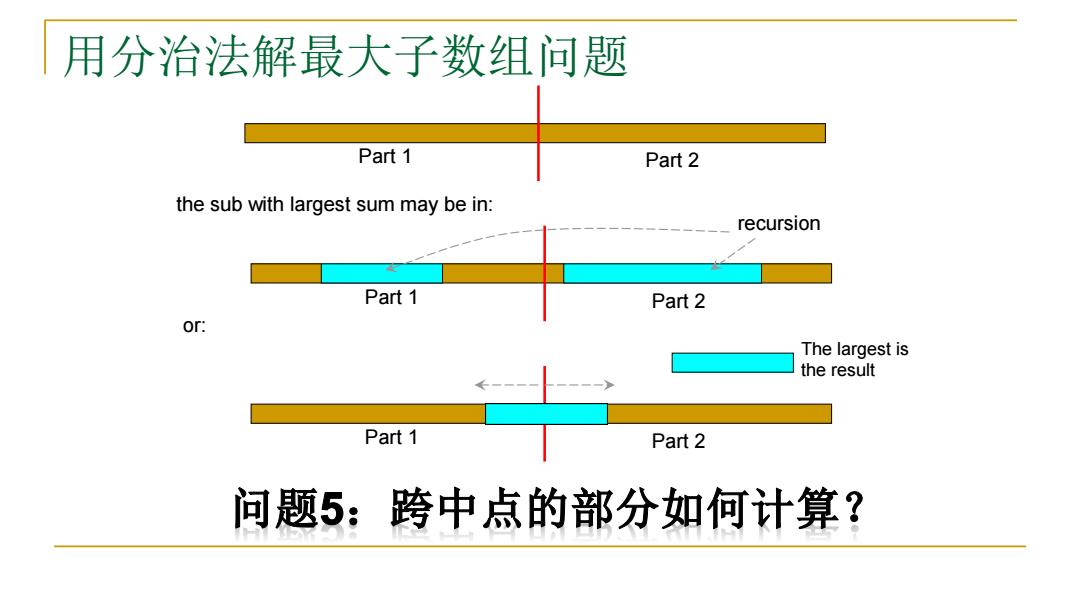
用分治法解最大子数组问题 Part 1 Part 2 the sub with largest sum may be in: recursion Part 1 Part 2 or: The largest is the result Part 1 Part 2 问题5:跨中点的部分如何计算?
用分治法解最大子数组问题 Part 1 Part 2 the sub with largest sum may be in: Part 1 Part 2 or: Part 1 Part 2 recursion The largest is the result

FIND-MAXIMUM-SUBARRAY(A,low,high) 非递归代价:常量 1 if high =low 2 return (low,high,Allow) /base case:only one element 3 else mid =(low high)/2 4 (left-low,lefi-high,left-sum)= 递归,理想状况下 FIND-MAXIMUM-SUBARRAY(A,low,mid) 问题规模是原来的 5 (right-low,right-high,right-sum)= 一半。 FIND-MAXIMUM-SUBARRAY (A,mid +1,high) 非递归代价: 6 (cross-low,cross-high,cross-sum)= 线性 FIND-MAX-CROSSING-SUBARRAY (A,low,mid,high) 7 if left-sm≥right-sum and left-sm≥cross--sum 8 return (lef-low,lef-high,lefi-sum) 9 elseif right-sum left-sum and right-sum cross-sum 非递归代价: 10 return(right-low,right-high,right-sum) 常量 11 else return (cross-low,cross-high,cross-sum) O(nlog n)
非递归代价:常量 递归,理想状况下 问题规模是原来的 一半。 非递归代价: 线性 非递归代价: 常量 O(nlogn)

矩阵乘法:似乎非得2() fA=a)and B(b)are squarenxmatrices,then in the product C=AB,we define the entry cij,for ij=1.2....by SQUARE-MATRIX-MULTIPLY(A,B) 1 n A.rows 2 let C be a new n x n matrix ci=∑akbj 3 for i lton 4 for j=Iton k三1 5 c4=0 6 for k 1to n 7 C时=C十aik·b财 return C
矩阵乘法:似乎非得(n 3 )

问题:你能就以下这句话,说清楚2,⊙,O和o 的区别吗? You might at first think that any matrix multiplication algorithm must take (n3) time,since the natural definition of matrix multiplication requires that many mul- tiplications.You would be incorrect,however:we have a way to multiply matrices in o(n3)time.In this section,we shall see Strassen's remarkable recursive algo- rithm for multiplying n x n matrices.It runs in (ns7)time,which we shall show in Section 4.5.Since lg 7 lies between 2.80 and 2.81,Strassen's algorithm runs in O(n281)time,which is asymptotically better than the simple SQUARE-MATRIX- MULTIPLY procedure
问题:你能就以下这句话,说清楚Ω,Θ,О和o 的区别吗?