
3.3沉降分离原理及方法 沉降是指在某种力的作用下,固粒相对于流体产生定向运 动而实现分离的操作过程。其依据是利用两相间密度的差异, 受力时其运动速度不同从而发生相对运动。进行沉降操作的作 用力可以是重力,也可以是惯性离心力,故沉降分为重力沉降 和离心沉降。衡量沉降进行的快慢程度通常用沉降速度来表示。 3.3.1重力沉降 依靠重力而进行的沉降过程。 3.3.1.1球形颗粒的自由沉降速度 自由沉降:发生在稀疏颗粒的流体中 干扰沉降:多发生在液态非均相物系中,沉降速度低。 以下讨论自由沉降过程
3.3 沉降分离原理及方法 沉降是指在某种力的作用下,固粒相对于流体产生定向运 动而实现分离的操作过程。其依据是利用两相间密度的差异, 受力时其运动速度不同从而发生相对运动。进行沉降操作的作 用力可以是重力,也可以是惯性离心力,故沉降分为重力沉降 和离心沉降。衡量沉降进行的快慢程度通常用沉降速度来表示。 3.3.1 重力沉降 依靠重力而进行的沉降过程。 3.3.1.1 球形颗粒的自由沉降速度 自由沉降:发生在稀疏颗粒的流体中 干扰沉降:多发生在液态非均相物系中,沉降速度低。 以下讨论自由沉降过程

设直径为d、密度为Ps的光滑球形颗粒在密度为p, 粘度为μ的静止流体中作自由沉降。此时颗粒受到阻 力、浮力和重力的作用,其中阻力是由摩擦引起的, 阻力Fd 随颗粒与流体间的相对运动速度而变,仿照管内流动 阻力计算式: 浮力F。 APr =6 Pu2 →E=P 2 A 2 Fa =5A Pu2 2.pu2 2 5π 4 2 则,受力情况: 重力:E=元dpg 重力Fg 6 浮力:E。=元dpg 6 阻力:E=6平 d2.pu2
设直径为d、密度为ρs的光滑球形颗粒在密度为ρ, 粘度为μ的静止流体中作自由沉降。此时颗粒受到阻 力、浮力和重力的作用,其中阻力是由摩擦引起的, 随颗粒与流体间的相对运动速度而变,仿照管内流动 阻力计算式: 浮力Fb 阻力Fd 重力Fg 2 u d 2 4 u F A 2 u A F 2 u p 2 2 2 d 2 d 2 f = = = = 则,受力情况: 2 u d 4 F d g 6 F d g 6 F 2 2 d 3 b s 3 g = = = 阻力: 浮力: 重力:

根据牛顿第二运动定律: Fg-Fb-Fd=ma 即: (p:0- 2 元dp,a 6 过程开始的瞬间,u=0,因此F。=0,故加速度具有最大值。 随着颗粒的下落,阻力增加,加速度减小。当u达到某一数值u: 后,使得重力与浮力、阻力达到平衡,即合力为零,此时加速 度为零。 因此,颗粒的沉降过程分为两个阶段: 加速阶段:u=0,Fd=0,a=amax ut,fot,al 等速阶段:u=ut时,Fa=FgFb,a=0
Fg -Fb-Fd=ma 即: 过程开始的瞬间,u=0,因此Fd=0,故加速度具有最大值。 随着颗粒的下落,阻力增加,加速度减小。当u达到某一数值ut 后,使得重力与浮力、阻力达到平衡,即合力为零,此时加速 度为零。 因此,颗粒的沉降过程分为两个阶段: •加速阶段:u=0,Fd=0,a=amax u↑,fd↑,a↓ •等速阶段:u=ut时,Fd=Fg -Fb,a=0 d a u d s g d s 3 2 3 2 4 2 6 ( ) 6 − − =

等速阶段里颗粒相对于流体的运动速度u称为“沉降速 度”。沉降速度就是加速阶段终了时颗粒相对于流体的速度, 因此亦称“终端速度”。 由于工业上沉降操作所处理的颗粒往往甚小,因而颗粒与流 体间的接触表面相对较大,故阻力随速度增长很快,可在短时 间内便与颗粒所受的净重力相平衡。所以在重力沉降过程中, 加速阶段常常可忽略不计。 等速阶段:a=0时,u=ut A3(P:-p8=d2.Pu8 2 .“.ut= 4d(P。-P)g 3Cp 上式称为重力沉降速度基本方程式
等速阶段里颗粒相对于流体的运动速度ut称为“沉降速 度” 。沉降速度就是加速阶段终了时颗粒相对于流体的速度, 因此亦称“终端速度” 。 由于工业上沉降操作所处理的颗粒往往甚小,因而颗粒与流 体间的接触表面相对较大,故阻力随速度增长很快,可在短时 间内便与颗粒所受的净重力相平衡。所以在重力沉降过程中, 加速阶段常常可忽略不计。 等速阶段:a=0时,u=ut 上式称为重力沉降速度基本方程式
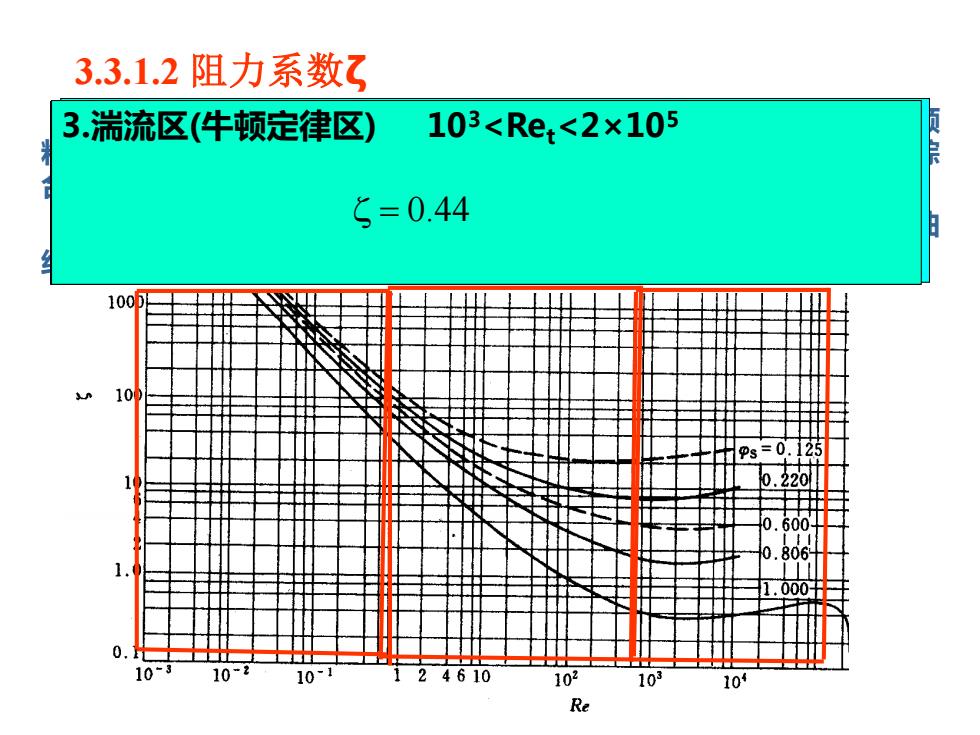
3.3.1.2阻力系数乙 3.湍流区(件顿定律区) 103<Re<2×105 5=0.44 00 0 10-3 10 10 4610 102 103 104 Re
3.3.1.2 阻力系数ζ 用前式计算沉降速度时,需先确定阻力系数ζ值。通过因次分析,ζ是颗 粒形状、颗粒与流体相对运动雷诺数Ret=dutρ/μ的函数,由实验测得的综 合结果在下图中示出。 对于球形颗粒的曲线,从图可看出,按Ret值大致分为三个区,各区内曲 线所对应的ζ可分别用相应的数学关系式表示。 1.滞流区(斯托克斯定律区) 10-4<Ret<1 Ret 24 = 2.过渡区(艾伦定律区) 1<Ret<103 0.6 Ret 18.5 = 3.湍流区(牛顿定律区) 103<Ret<2×105 = 0.44