
第4卷第2期 智能系统学报 Vol 4 Ng 2 2009年4月 CAA I Transactions on Intelligent Systems Apr 2009 频繁模式挖掘的约束算法 孟彩霞 西安邮电学院计算机系,陕西西安710065) 摘要:在频繁模式挖据过程中能够动态改变约束的算法比较少.提出了一种基于约束的频繁模式挖掘算法MCFP MC℉P首先按照约束的性质来建立频繁模式树,并且只需扫描一遍数据库,然后建立每个项的条件树挖掘以该项为 前缀的最大频繁模式,并用最大模式树来存储,最后根据最大模式来找出所有支持度明确的频繁模式.MC℉P算法允 许用户在挖掘频繁模式过程中动态地改变约束.实验表明,该算法与C℉P算法相比是很有效的 关键词:频繁模式挖掘:动态约束:频繁项集:最大频繁模式 中图分类号:TP311文献标识码:A文章编号:1673-4785(2009)02014206 A frequent pa ttern m in ing a lgorithm ba sed on con stra n ts MENG Cai-xia (Deparment of Computer Science,Xi'an University of Posts&Telecommunications,Xi'an 710065,China) Abstract:Most algorithms don't allow users to dynam ically change constraints in the process of m ining frequent pattems A new algorithm,constrain-based frequent pattems m ining,was developed to provide frequent pattem mining with constraints First,the algorithm constructs the FP-tree (frequent pattem tree)according to the de- scending or ascending order of constraints,and in this process the database only needs to be scanned once Second- ly,the conditional tree of each item was established to m ine maxmal frequent pattem with this tem as a prefix, and the maximal frequent pattems were stored Finally,all frequent pattems with precise support degrees were dis- covered according to the maxmal frequent pattems The significance of thismethod is that this algorithm allows us- ers to dynam ically change constraints during the process Expermental outcomes showed that the proposed algo- rithm is more efficient than the algorithm of CFP. Keywords:frequent pattems m ining dynam ic constraints frequent item set maxmal frequent pattem 关联规则挖掘是数据挖掘领域研究的重要课进,但是同样存在着这样的问题l,s).Hen等人提出 题.关联规则挖掘问题的解决分为2步:1)找出所 了基于FP-tree结构的不用产生候选项集的FP- 有的频繁项集缬繁模式);2)由频繁项集产生强关 govh算法161,该算法只需扫描2次数据库来建立 联规则.这2步中,频繁项集挖掘是基本步骤,是关 FP-tree,大大提高了挖掘效率.目前,出现了有关挖 联规则挖掘问题的核心1).Agrawal等人提出了经 掘最大频繁模式算法、基于约束的频繁模式挖掘 典的Apriori算法,但是该算法要产生大量的候选 算法[8等.对于交互式频繁模式挖掘,Zhu等人提出 项集并需多次扫描数据库,大大降低了算法的性能. 了UFP-Te算法I,它只是针对支持度不断变化 后来一些类Apriori算法虽然对Apriori做了很多改 的交互式挖掘算法.Leng把约束和交互式相结合提 出了CFP算法o),该算法允许用户在挖掘过程中 收稿日期:2008-12-16 基金项目:陕西省自然科学基金资助项目(2004283);西安市科技创 动态改变约束,且不必重新扫描数据库,但是在找频 新支撑应用发展研究计划资助项目(Y℉07024). 通信作者:孟彩霞.Email:mexmcx(@xiyou edu cn 繁项集时,需要不断建立条件树,占用了大量内存: 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 4卷第 2期 智 能 系 统 学 报 Vol. 4 №. 2 2009年 4月 CAA I Transactions on Intelligent System s Ap r. 2009 频繁模式挖掘的约束算法 孟彩霞 (西安邮电学院 计算机系 ,陕西 西安 710065) 摘 要 :在频繁模式挖掘过程中能够动态改变约束的算法比较少. 提出了一种基于约束的频繁模式挖掘算法 MCFP. MCFP首先按照约束的性质来建立频繁模式树 ,并且只需扫描一遍数据库 ,然后建立每个项的条件树 ,挖掘以该项为 前缀的最大频繁模式 ,并用最大模式树来存储 ,最后根据最大模式来找出所有支持度明确的频繁模式. MCFP算法允 许用户在挖掘频繁模式过程中动态地改变约束. 实验表明 ,该算法与 iCFP算法相比是很有效的. 关键词 :频繁模式挖掘 ;动态约束 ;频繁项集 ;最大频繁模式 中图分类号 : TP311 文献标识码 : A 文章编号 : 167324785 (2009) 0220142206 A frequent pattern m in ing algor ithm based on constra ints MENG Cai2xia (Department of Computer Science, Xi’an University of Posts & Telecommunications, Xi’an 710065, China) Abstract:Most algorithm s don’t allow users to dynam ically change constraints in the p rocess of m ining frequent patterns. A new algorithm, constrain2based frequent patterns m ining, was developed to p rovide frequent pattern m ining with constraints. First, the algorithm constructs the FP2tree ( frequent pattern tree) according to the de2 scending or ascending order of constraints, and in this p rocess the database only needs to be scanned once. Second2 ly, the conditional tree of each item was established to m ine maximal frequent pattern with this term as a p refix, and the maximal frequent patternswere stored. Finally, all frequent patternswith p recise support degreeswere dis2 covered according to the maximal frequent patterns. The significance of thismethod is that this algorithm allows us2 ers to dynam ically change constraints during the p rocess. Experimental outcomes showed that the p roposed algo2 rithm is more efficient than the algorithm of iCFP. Keywords: frequent patterns m ining; dynam ic constraints; frequent item set; maximal frequent pattern 收稿日期 : 2008212216. 基金项目 :陕西省自然科学基金资助项目 (2004f283) ; 西安市科技创 新支撑 —应用发展研究计划资助项目 ( YF07024). 通信作者 :孟彩霞. E2mail: mcxmcx@xiyou. edu. cn 关联规则挖掘是数据挖掘领域研究的重要课 题. 关联规则挖掘问题的解决分为 2步 : 1)找出所 有的频繁项集 (频繁模式 ) ; 2)由频繁项集产生强关 联规则. 这 2步中 , 频繁项集挖掘是基本步骤 ,是关 联规则挖掘问题的核心 [ 123 ] . Agrawal等人提出了经 典的 Ap riori算法 [ 4 ] ,但是该算法要产生大量的候选 项集并需多次扫描数据库 ,大大降低了算法的性能. 后来一些类 Ap riori算法虽然对 Ap riori做了很多改 进 ,但是同样存在着这样的问题 [ 1, 5 ] . Hen等人提出 了基于 FP2tree 结构的不用产生候选项集的 FP2 growth算法 [ 6 ] ,该算法只需扫描 2次数据库来建立 FP2tree,大大提高了挖掘效率. 目前 ,出现了有关挖 掘最大频繁模式算法 [ 7 ]、基于约束的频繁模式挖掘 算法 [ 8 ]等. 对于交互式频繁模式挖掘 , Zhu等人提出 了 IUFP2Tree算法 [ 9 ] ,它只是针对支持度不断变化 的交互式挖掘算法. Leng把约束和交互式相结合提 出了 iCFP算法 [ 10 ] ,该算法允许用户在挖掘过程中 动态改变约束 ,且不必重新扫描数据库 ,但是在找频 繁项集时 ,需要不断建立条件树 ,占用了大量内存

第2期 孟彩霞:频繁模式挖掘的约束算法 ·143· 提出了一个在频繁模式挖掘过程中可以改变约 调性约束 束的算法,该算法不用反复建立条件树,且在建树时 定义6单调性(monotone)约束.如果项集X 是按照约束的大小顺序来建立的,并且每次只有一 满足约束0,它的所有超集也都满足,则日是单调性 个条件树存在于内存中,挖掘完该条件树后立即释 约束 放,和现有的CFP相比节省了大量内存.为了验证 定义7简洁性(succinct)约束.如果可以直接 算法的性能,进行了一系列的实验来评价算法,实验 精确地产生满足约束的所有项集,而不用产生不满 表明该算法的优越性是明显的」 足约束的项集,则该约束日为简洁性约束, 例如,mn(XA)≥v是简洁反单调性约束 1问题定义 max(XA)≥v是简洁单调性约束 设1={,五,}是n个不同项目的集合, 2算法MCFP 其中)=1,2.,n)是数据单项.事务数据库 DB=<1,I2,T>,其中每个事务T1=1,2 算法MCFP是针对CFP存在的问题(即不断建 m)是中一组项目的集合,即工三1T有一个 立条件树)而提出的一种改进方法。 惟一的标识符TD. 21数据结构 定义1对于一个集合X,如果X三1且X包 表1和表2分别是一个事务数据库和一个数据 含k个项目,则称X为k-项集,简称为项集 单项的属性表.这里假设数据单项有属性A和B. 定义2如果项集X三工,则称事务T包含项 表1事务数据库 集X:项集X在事务数据库DB中的支持度,记为 Table 1 Transaction datbase SupDa(X),即事务数据库DB中包含项集X的事务 TD Items 个数 1 abed 2 bdf 定义3如果项集X在事务数据库DB中的支 3 abce 持度Supe(X)不小于用户或专家给定的最小支持 4 abde 度阈值δ则称项集X为频繁项集倾繁模式):反之 称之为非频繁项集 表2数据单项的属性表 定义4给定最小支持度δ,对于项集X三1若 Table 2 A ttr butes of da ta item Sups(X)≥6,且对于廿Y(Y∈I∧XCY),均有 item A B Supe(Y)<6,则称X为DB中的最大频繁项集或 60 300 称最大频繁模式).也就是说,如果频繁项集X的所 B 30 400 C 35 500 有超集都是非频繁项集,那么X为最大频繁项集 D 40 450 性质1频繁项集的任何真子集都不是最大频 E 55 600 繁项集 F 65 380 性质2频繁项集的任何子集都是频繁项集」 这里按照属性A上值的大小顺序来建立P 显然,任何频繁项集都是某一个最大频繁项集 tree,这样仅需扫描一遍数据库,然后建立满足简洁 的子集,所以可以把挖掘所有频繁项集的问题转化 性约束的项的条件树.假设简洁性约束为C,= 为挖掘最大频繁项集的问题 mm(sA)≥30,最小支持度6=2 对于项目集合中的每个单项可能有预先定义 在FP-tee中设计了2个数据结构:List和FP- 的属性,例如有属性A、B.定义在项集上的约束0∈ tree List)用于存储可能的频繁单项,FP-tree用于存 {tue,false},如果0(X)=tnue,则项集X满足该约 储可能的频繁项集,具体说明如下: 束.目前常用的约束分为3大类:反单调性约束、单 List一个三元组表.每个三元组(A,item 调性约束和简洁性约束 name,8),其中A是数据单项属性表中有约束的属 定义5反单调性(antimonotone)约束.如果项 性上的分量值,item-name是单项的名称,8是该项 集X不满足约束日,它的超集也不满足,则0是反单 的支持度.Ls表中三元组按照A上的值从大到小 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
提出了一个在频繁模式挖掘过程中可以改变约 束的算法 ,该算法不用反复建立条件树 ,且在建树时 是按照约束的大小顺序来建立的 ,并且每次只有一 个条件树存在于内存中 ,挖掘完该条件树后立即释 放 ,和现有的 iCFP相比节省了大量内存. 为了验证 算法的性能 ,进行了一系列的实验来评价算法 ,实验 表明该算法的优越性是明显的. 1 问题定义 设 I = { i1 , i2 , …, in } 是 n个不同项目的集合 , 其中 ij ( j = 1, 2, …, n) 是数据单项. 事务数据库 DB = < T1 , T2 , …, Tm >,其中每个事务 Tj ( j = 1, 2, …, m ) 是 I中一组项目的集合 ,即 Tj Α I, Tj有一个 惟一的标识符 TID. 定义 1 对于一个集合 X,如果 X Α I,且 X 包 含 k个项目 ,则称 X 为 k - 项集 ,简称为项集. 定义 2 如果项集 X Α Tj ,则称事务 Tj包含项 集 X; 项集 X 在事务数据库 DB 中的支持度 , 记为 SupDB (X ) ,即事务数据库 DB 中包含项集 X 的事务 个数. 定义 3 如果项集 X 在事务数据库 DB 中的支 持度 SupDB (X ) 不小于用户或专家给定的最小支持 度阈值 δ,则称项集 X为频繁项集 (频繁模式 ) ;反之 称之为非频繁项集. 定义 4 给定最小支持度δ,对于项集 X Α I,若 SupDB (X ) ≥δ,且对于 Π Y ( Y Α I ∧ X < Y) ,均有 SupDB ( Y) <δ,则称 X为 DB 中的最大频繁项集 (或 称最大频繁模式 ). 也就是说 ,如果频繁项集 X 的所 有超集都是非频繁项集 ,那么 X为最大频繁项集. 性质 1 频繁项集的任何真子集都不是最大频 繁项集. 性质 2 频繁项集的任何子集都是频繁项集. 显然 , 任何频繁项集都是某一个最大频繁项集 的子集 , 所以可以把挖掘所有频繁项集的问题转化 为挖掘最大频繁项集的问题. 对于项目集合 I中的每个单项可能有预先定义 的属性 ,例如有属性 A、B. 定义在项集上的约束 θ∈ { true, false} ,如果 θ(X ) = true,则项集 X满足该约 束. 目前常用的约束分为 3大类 :反单调性约束、单 调性约束和简洁性约束. 定义 5 反单调性 ( anti2monotone)约束. 如果项 集 X不满足约束 θ,它的超集也不满足 ,则 θ是反单 调性约束. 定义 6 单调性 (monotone)约束. 如果项集 X 满足约束 θ,它的所有超集也都满足 ,则 θ是单调性 约束. 定义 7 简洁性 ( succinct)约束. 如果可以直接 精确地产生满足约束的所有项集 ,而不用产生不满 足约束的项集 ,则该约束 θ为简洁性约束. 例如 , m in (X. A ) ≥ v是简洁反单调性约束 , max (X. A ) ≥ v是简洁单调性约束. 2 算法 MCFP 算法 MCFP是针对 iCFP存在的问题 (即不断建 立条件树 )而提出的一种改进方法. 2. 1 数据结构 表 1和表 2分别是一个事务数据库和一个数据 单项的属性表. 这里假设数据单项有属性 A和 B. 表 1 事务数据库 Table 1 Tran saction da taba se TID Item s 1 abcd 2 bdf 3 abce 4 abde 表 2 数据单项的属性表 Table 2 A ttr ibutes of da ta item item A B A 60 300 B 30 400 C 35 500 D 40 450 E 55 600 F 65 380 这里按照属性 A 上值的大小顺序来建立 FP2 tree,这样仅需扫描一遍数据库 ,然后建立满足简洁 性约束的项的条件树. 假设简洁性约束为 Cs = m in (s. A ) ≥30,最小支持度 δ = 2. 在 FP2tree中设计了 2个数据结构 : L ist和 FP2 tree. L ist用于存储可能的频繁单项 , FP2tree用于存 储可能的频繁项集 ,具体说明如下 : L ist:一个三元组表. 每个三元组 ( A , item2 name, δ) ,其中 A是数据单项属性表中有约束的属 性上的分量值 , item2name是单项的名称 , δ是该项 的支持度. L ist表中三元组按照 A 上的值从大到小 第 2期 孟彩霞 :频繁模式挖掘的约束算法 ·143·

·144 智能系统学报 第4卷 或从小到大)顺序排列 调性约束)或由小到大(简洁反单调性约束)创建 FP-tree:一个字典树,每个节点是一个对偶(r List表; tem-name,.F),其中item-name是项名,F是由FP- 2)初始化FP-tree,根指针T为“NULL”: tree的根节点至当前节点的路径上所有项组成的项 3)ForDB中的每个事务t 集的支持度 ①事务的项集已经是T的一个分支(仔 2.2建立FP-tree 树){ 建立FP-tree的步骤如下: ② 该分支上的节点N的支持度增加1; 1)把项按照A的值从大到小顺序排序,放进 ③ List中该项集的每个单项的支持度增加 List表中 1,} 2)扫描事务数据库,根据List中项的顺序建立 ④ Else FP-tree,把每次涉及到的项的支持度(卿List表中项 ⑤ 创建新的节点N,存放事务T的项集: 的δ值)加1,直到最后一个事务,同时建立相同项 ⑥ 节点N和T连接起来; 之间的连接.此时包含非频繁项的树建立完毕, ⑦ 具有相同项的节点连接起来;} 如图所示 ⑧Endf List Root ⑨End For 65 4)fN的支持度小于最小支持度 60a 5)删除节点N以及和N有关的连接: 55e 2 6)End If 40d3 23建立满足约束的条件树找出最大频繁模式 e:I 35 首先从Lst表中最后一项开始,判断各项是否 30b4 b:1-=b:1 满足给定的条件.如果不满足,则不用建立该项的条 件树,这样就把约束放到了挖掘过程中,根据约束的 图1包含非频繁项的树的结构 性质来降低搜索空间.如果找到满足约束的项,则建 Fig 1 Tree included infrequent item set 立该项的条件树,并把该树中的非频繁项即局部非 3)查Ls表去掉表中非频繁项.当去掉非频繁项 频繁项去掉.由图2可知,最后一项是b,b满足假设 时,根据连接重新调整树的结构.由图1中List可知f 的简洁性约束C,=min (sA)≥30,b的条件树 的支持度小于2,去掉项f后的FP-tree如图2所示. 如图3所示.由于b的条件树中没有局部非频繁项, Root 所以不用再重新调整该树的结构 List e:2 h4 60 c:I 30b 4 h 图2FP-tree结构 图3b的条件树 Fig 2 FP-tree structure Fig 3 Condition-tree of b 算法1建立FP-tree的算法】 然后用该树的分支两两相交来得到局部最大 输入:DB,最小支持度8,简洁性约束; 频繁模式.例如b的条件树前2个分支bcae:1和 输出:FP-tee bcda:1相交得到bca:2然后按照支持度由大到小 方法: 的顺序插入到最大模式树中.最大模式树初始值为 1)按照每个单项的属性A值由大到小(简洁单 空,如果某项集已存在于最大模式树中或是已存在 的最大模式树的子集,则不再插入该项集.挖掘完b 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
(或从小到大 )顺序排列. FP2tree:一个字典树 ,每个节点是一个对偶 ( i2 tem2name, F ) ,其中 item2name是项名 , F是由 FP2 tree的根节点至当前节点的路径上所有项组成的项 集的支持度. 2. 2 建立 FP2tree 建立 FP2tree的步骤如下 : 1)把项按照 A 的值从大到小顺序排序 ,放进 List表中. 2)扫描事务数据库 ,根据 L ist中项的顺序建立 FP2tree,把每次涉及到的项的支持度 (即 L ist表中项 的 δ值 )加 1,直到最后一个事务 ,同时建立相同项 之间的连接. 此时包含非频繁项的树建立完毕 , 如图 1所示. 图 1 包含非频繁项的树的结构 Fig. 1 Tree included infrequent item set 3)查 List表去掉表中非频繁项.当去掉非频繁项 时 ,根据连接重新调整树的结构. 由图 1中 List可知 f 的支持度小于 2,去掉项 f后的 FP2tree如图 2所示. 图 2 FP2tree结构 Fig. 2 FP2tree structure 算法 1 建立 FP2tree的算法. 输入 : DB, 最小支持度 δ,简洁性约束 ; 输出 : FP2tree 方法 : 1)按照每个单项的属性 A值由大到小 (简洁单 调性约束 )或由小到大 (简洁反单调性约束 )创建 List表 ; 2)初始化 FP2tree,根指针 T为“NULL”; 3) For DB中的每个事务 t ① If事务 t的项集已经是 T的一个分支 (子 树 ) { ② 该分支上的节点 N 的支持度增加 1; ③ List中该项集的每个单项的支持度增加 1; } ④ Else { ⑤ 创建新的节点 N,存放事务 T的项集; ⑥ 节点 N 和 T连接起来 ; ⑦ 具有相同项的节点连接起来 ; } ⑧ End If ⑨End For 4) IfN 的支持度小于最小支持度 5)删除节点 N 以及和 N 有关的连接 ; 6) End If 2. 3 建立满足约束的条件树找出最大频繁模式 首先从 L ist表中最后一项开始 ,判断各项是否 满足给定的条件. 如果不满足 ,则不用建立该项的条 件树 ,这样就把约束放到了挖掘过程中 ,根据约束的 性质来降低搜索空间. 如果找到满足约束的项 ,则建 立该项的条件树 ,并把该树中的非频繁项即局部非 频繁项去掉. 由图 2可知 ,最后一项是 b, b满足假设 的简洁性约束 Cs = m in (s. A ) ≥ 30, b的条件树 如图 3所示. 由于 b的条件树中没有局部非频繁项 , 所以不用再重新调整该树的结构. 图 3 b的条件树 Fig. 3 Condition2tree of b 然后用该树的分支两两相交来得到局部最大 频繁模式. 例如 b的条件树前 2个分支 bcae: 1和 bcda: 1相交得到 bca: 2. 然后按照支持度由大到小 的顺序插入到最大模式树中. 最大模式树初始值为 空 ,如果某项集已存在于最大模式树中或是已存在 的最大模式树的子集 ,则不再插入该项集. 挖掘完 b ·144· 智 能 系 统 学 报 第 4卷

第2期 孟彩霞:频繁模式挖掘的约束算法 ·145- 的条件树后得到的最大模式树如图4所示 6) 把这些路径插入M的条件树中; Root 7) 把条件树中的相同项连接起来; 8) 调用m ining(M-conditional tree); 9) 释放M的条件树;}} 10)最大频繁模式即为MFT的每个分支 算法3 m ining(M-conditional tree)算法 d:2.c:2e:2 输入:条件树M-conditional tree,最小支持度8; 输出:局部最大频繁模式(MFT) 图4挖掘完b条件树后的最大模式树 1)IMFT=: Fig 4 Maxmal pattems tree after m ining b 2)M的条件树的每个分支两两相交得到局部 同理,分别建立cda、e的条件树,依次得到局 频繁模式P 部最大模式插入到最大模式中,最后得到的最大模 3)按照支持度递减的顺序把P插入到MFT中; 式树即为图4所示。 4)如果该局部频繁模式存在于MFT中或是 由图4可知,最后的最大频繁模式为bac2、 MFT的子集: bae:2、bad2 5)不需要插入该局部频繁模式: 如果还需要其他的频繁模式,只需从最大频繁 模式中得到所需要的模式,因为这些模式肯定是最 3MCFP处理动态约束 大频繁模式的子集.所以得到所有的频繁模式很容 当约束变化时约束范围可能是以前范围的超集 易,但得到它们的支持度却不容易,因为最大模式中 也可能是子集.约束范围由小变大时称为松约束性 不包含它们的支持度信息.目前许多算法都是在找 变化(relaxing change),约束范围由大变小时称为紧 到最大模式后再重新扫描一遍数据库来得到所有频 约束性变化(tighting change) 繁模式的支持度信息,这样在重新扫描数据库时算 31处理紧约束性的动态变化 法的性能就降低了.针对这一问题,MCFP算法把支 持度的信息都保存在Lst表中,所以不用重新扫描 设约束由Cu=min(sA)≥30变为Caw= 数据库就很容易得到所有频繁模式的信息.例如,由 min(sA)≥40,显然有SSaw∈SSu,其中SSn是指 新约束的范围,SS是指以前的约束范围所以只需 最大频繁模式bac可以知道它的子模式有ba、bc 在最大模式树中去掉不满足约束的项,即hc删除 αc并且根据简洁性约束的性质,直接就能判断这些 子模式都满足约束条件.现在最主要的就是得到它 bc后的最大模式树如图5所示 Root 们的支持度来判断它们是否频繁.以计算bc的支持 度为例,由List表中包含的频繁项的信息可得b:4、 c2,所以b的支持度以这2项中支持度小的一项为 准,即bc2按照这种方法,最后所有的满足约束的 d:2 :2 频繁模式为ba:3、bd:3、ad:2、bc:2、be2、ae2、bac 2、bae2、badk2 图5约束化后的最大模式树 算法2建立MFT(maxmal frequent pattem Fig 5 Maxmal pattems tree after changed constraint tree). 由图5可得满足约束的最大模式为ad:2 输入:FP-tree最小支持度8、约束; ae2由最大模式可得满足约束的所有频繁模式有 输出:最大频繁模式MFT a:3、d:3、e:3 1)M=List表中的最后一项; 3.2处理松约束性的动态变化 2)M的条件树M-conditional tree=中; 设约束由CoM=min(sA)≥40变为Cnaw= 3)For(i=1:i<=项的个数:i++){; min(sA)≥30,则SSw2SSu.这样b和c也满足约 4)if(min(M.A)≥30){ 束条件了,只需再挖掘6c的条件树,最后把局部频 5) 找出含有项M的所有路径; 繁模式插入到Ca=mim(sA)≥40约束时的最大 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
的条件树后得到的最大模式树如图 4所示. 图 4 挖掘完 b条件树后的最大模式树 Fig. 4 Maximal patterns tree after mining b 同理 ,分别建立 c、d、a、e的条件树 ,依次得到局 部最大模式插入到最大模式中 ,最后得到的最大模 式树即为图 4所示. 由图 4 可知 ,最后的最大频繁模式为 bac: 2、 bae: 2、bad: 2. 如果还需要其他的频繁模式 ,只需从最大频繁 模式中得到所需要的模式 ,因为这些模式肯定是最 大频繁模式的子集. 所以得到所有的频繁模式很容 易 ,但得到它们的支持度却不容易 ,因为最大模式中 不包含它们的支持度信息. 目前许多算法都是在找 到最大模式后再重新扫描一遍数据库来得到所有频 繁模式的支持度信息 ,这样在重新扫描数据库时算 法的性能就降低了. 针对这一问题 ,MCFP算法把支 持度的信息都保存在 List表中 ,所以不用重新扫描 数据库就很容易得到所有频繁模式的信息. 例如 ,由 最大频繁模式 bac可以知道它的子模式有 ba、bc、 ac,并且根据简洁性约束的性质 ,直接就能判断这些 子模式都满足约束条件. 现在最主要的就是得到它 们的支持度来判断它们是否频繁. 以计算 bc的支持 度为例 ,由 L ist表中包含的频繁项的信息可得 b: 4、 c: 2,所以 bc的支持度以这 2项中支持度小的一项为 准 ,即 bc: 2. 按照这种方法 ,最后所有的满足约束的 频繁模式为 ba: 3、bd: 3、ad: 2、bc: 2、be: 2、ae: 2、bac: 2、bae: 2、bad: 2. 算法 2 建立 MFT (maximal frequent pattern tree). 输入 : FP2tree、最小支持度 δ、约束 ; 输出 :最大频繁模式 MFT. 1) M =L ist表中的最后一项 ; 2) M 的条件树 M2conditional tree = < ; 3) For( i = 1; i < =项的个数; i ++ ) { ; 4) if( m in ( M. A ) ≥30) { 5) 找出含有项 M 的所有路径 ; 6) 把这些路径插入 M 的条件树中 ; 7) 把条件树中的相同项连接起来 ; 8) 调用 m ining( M 2conditional tree) ; 9) 释放 M 的条件树 ; } } 10)最大频繁模式即为 MFT的每个分支. 算法 3 m ining( M 2conditional tree)算法. 输入:条件树 M 2conditional tree,最小支持度δ; 输出 :局部最大频繁模式 (LMFT) 1) LMFT = <; 2) M 的条件树的每个分支两两相交得到局部 频繁模式 P; 3) 按照支持度递减的顺序把 P插入到 MFT中; 4) 如果该局部频繁模式存在于 MFT中或是 MFT的子集 ; 5) 不需要插入该局部频繁模式. 3 MCFP处理动态约束 当约束变化时约束范围可能是以前范围的超集 也可能是子集. 约束范围由小变大时称为松约束性 变化 ( relaxing change) ,约束范围由大变小时称为紧 约束性变化 ( tighting change). 3. 1 处理紧约束性的动态变化 设约束由 Cold = m in ( s. A ) ≥30 变为 Cnew = m in (s. A ) ≥40,显然有 SSnew Α SSold ,其中 SSnew是指 新约束的范围 , SSold是指以前的约束范围. 所以只需 在最大模式树中去掉不满足约束的项 ,即 b、c. 删除 b、c后的最大模式树如图 5所示. 图 5 约束化后的最大模式树 Fig. 5 Maximal patterns tree after changed constraint 由图 5 可得满足约束的最大模式为 ad: 2、 ae: 2. 由最大模式可得满足约束的所有频繁模式有 a: 3、d: 3、e: 3. 3. 2 处理松约束性的动态变化 设 约 束 由 Cold = m in (s. A ) ≥40变 为 Cnew = m in (s. A ) ≥30,则 SSnew Β SSold . 这样 b和 c也满足约 束条件了 ,只需再挖掘 b、c的条件树 ,最后把局部频 繁模式插入到 Cold =m in ( s. A ) ≥40约束时的最大 第 2期 孟彩霞 :频繁模式挖掘的约束算法 ·145·
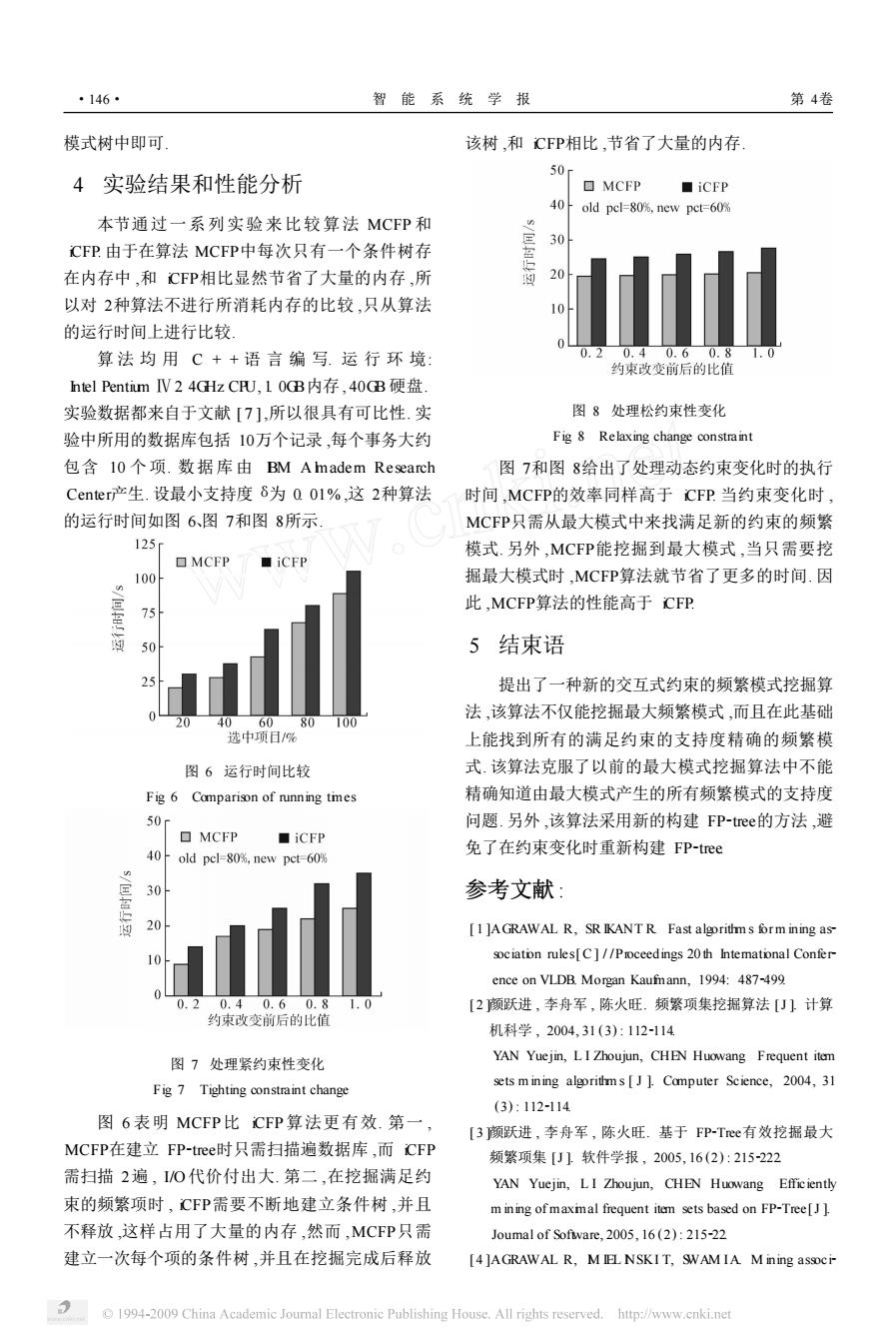
·146 智能系统学报 第4卷 模式树中即可 该树,和CFP相比,节省了大量的内存 4实验结果和性能分析 50r MCFP ■iCFP 40 old pcl=80%,new pct=60% 本节通过一系列实验来比较算法MCFP和 30 CFP由于在算法MCFP中每次只有一个条件树存 在内存中,和C℉P相比显然节省了大量的内存,所 20 以对2种算法不进行所消耗内存的比较,只从算法 的运行时间上进行比较 算法均用C++语言编写.运行环境 0.20.40.60.8 约束改变前后的比值 ntel Pentium IV24 Hz CRU,10GB内存,40GB硬盘. 实验数据都来自于文献【7],所以很具有可比性.实 图8处理松约束性变化 验中所用的数据库包括10万个记录,每个事务大约 Fig 8 Relaxing change constraint 包含l0个项.数据库由BM Amadem Research 图7和图8给出了处理动态约束变化时的执行 Center产生.设最小支持度8为Q01%,这2种算法 时间,MCFP的效率同样高于CFP当约束变化时, 的运行时间如图6、图7和图8所示 MCFP只需从最大模式中来找满足新的约束的频繁 125 模式.另外,MCFP能挖掘到最大模式,当只需要挖 口MCFP ■iCFP 100 掘最大模式时,MCFP算法就节省了更多的时间.因 此,MCFP算法的性能高于CFP 75 50 5结束语 提出了一种新的交互式约束的频繁模式挖掘算 法,该算法不仅能挖掘最大频繁模式,而且在此基础 20 406080 00 选中项日/% 上能找到所有的满足约束的支持度精确的频繁模 图6运行时间比较 式.该算法克服了以前的最大模式挖掘算法中不能 Fig 6 Comparison of running tmes 精确知道由最大模式产生的所有频繁模式的支持度 50r 问题.另外,该算法采用新的构建FP-tree的方法,避 ▣MCFP ■iCFP 40 old pcl=80%,new pct=60% 免了在约束变化时重新构建FP-tree 30 参考文献: 20 1 ]A GRAWAL R,SR IKANT R Fast algorithms orm ining as- sociaton rules[C]//Proceedings 20 th Intemational Confer ence on VLDB.Morgan Kaufnann,1994:487-499 0.20.40.60.8 1.0 [2颜跃进,李舟军,陈火旺.频繁项集挖掘算法[J)计算 约束改变前后的比值 机科学,2004,31(3):112-114 图7处理紧约束性变化 YAN Yuejin,LI Zhoujun,CHEN Huowang Frequent item Fig 7 Tighting constraint change sets m ining algorithms [J ]Computer Science,2004,31 (3):112-114 图6表明MCFP比CFP算法更有效.第一, [3颜跃进,李舟军,陈火旺.基于FP-Tee有效挖掘最大 MCFP在建立FP-tee时只需扫描遍数据库,而CFP 频繁项集[J]软件学报,2005,16(2):215-222 需扫描2遍,1/O代价付出大.第二,在挖掘满足约 YAN Yuejin,LI Zhoujun,CHEN Huowang Efficiently 束的频繁项时,CFP需要不断地建立条件树,并且 m ining ofmaxmal frequent item sets based on FP-Tree[J. 不释放,这样占用了大量的内存,然而,MCFP只需 Joumal of Sofware,2005,16(2):215-22 建立一次每个项的条件树,并且在挖掘完成后释放 [4 ]AGRAWAL R,M IEL NSKI T,SWAMIA M ining associ 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
模式树中即可. 4 实验结果和性能分析 本节通过一系列实验来比较算法 MCFP 和 iCFP. 由于在算法 MCFP中每次只有一个条件树存 在内存中 ,和 iCFP相比显然节省了大量的内存 ,所 以对 2种算法不进行所消耗内存的比较 ,只从算法 的运行时间上进行比较. 算 法 均 用 C + + 语 言 编 写. 运 行 环 境: Intel Pentium Ⅳ2. 4GHz CPU, 1. 0GB内存 , 40GB 硬盘. 实验数据都来自于文献 [ 7 ],所以很具有可比性. 实 验中所用的数据库包括 10万个记录 ,每个事务大约 包含 10 个项. 数据库由 IBM A lmadern Research Center产生. 设最小支持度 δ为 0. 01% ,这 2种算法 的运行时间如图 6、图 7和图 8所示. 图 6 运行时间比较 Fig. 6 Comparison of running times 图 7 处理紧约束性变化 Fig. 7 Tighting constraint change 图 6 表明 MCFP比 iCFP算法更有效. 第一 , MCFP在建立 FP2tree时只需扫描遍数据库 ,而 iCFP 需扫描 2遍 , I/O代价付出大. 第二 ,在挖掘满足约 束的频繁项时 , iCFP需要不断地建立条件树 ,并且 不释放 ,这样占用了大量的内存 ,然而 ,MCFP只需 建立一次每个项的条件树 ,并且在挖掘完成后释放 该树 ,和 iCFP相比 ,节省了大量的内存. 图 8 处理松约束性变化 Fig. 8 Relaxing change constraint 图 7和图 8给出了处理动态约束变化时的执行 时间 ,MCFP的效率同样高于 iCFP. 当约束变化时 , MCFP只需从最大模式中来找满足新的约束的频繁 模式. 另外 ,MCFP能挖掘到最大模式 ,当只需要挖 掘最大模式时 ,MCFP算法就节省了更多的时间. 因 此 ,MCFP算法的性能高于 iCFP. 5 结束语 提出了一种新的交互式约束的频繁模式挖掘算 法 ,该算法不仅能挖掘最大频繁模式 ,而且在此基础 上能找到所有的满足约束的支持度精确的频繁模 式. 该算法克服了以前的最大模式挖掘算法中不能 精确知道由最大模式产生的所有频繁模式的支持度 问题. 另外 ,该算法采用新的构建 FP2tree的方法 ,避 免了在约束变化时重新构建 FP2tree. 参考文献 : [ 1 ]AGRAWAL R, SR IKANT R. Fast algorithm s formining as2 sociation rules[ C ] / /Proceedings 20 th International Confer2 ence on VLDB. Morgan Kaufmann, 1994: 4872499. [ 2 ]颜跃进 , 李舟军 , 陈火旺. 频繁项集挖掘算法 [J ]. 计算 机科学 , 2004, 31 (3) : 1122114. YAN Yuejin, L I Zhoujun, CHEN Huowang. Frequent item sets m ining algorithm s [ J ]. Computer Science, 2004, 31 (3) : 1122114. [ 3 ]颜跃进 , 李舟军 , 陈火旺. 基于 FP2Tree有效挖掘最大 频繁项集 [J ]. 软件学报 , 2005, 16 (2) : 2152222. YAN Yuejin, L I Zhoujun, CHEN Huowang. Efficiently m ining of maximal frequent item sets based on FP2Tree[J ]. Journal of Software, 2005, 16 (2) : 215222. [ 4 ]AGRAWAL R, IM IEL INSKI T, SWAM IA. M ining associ2 ·146· 智 能 系 统 学 报 第 4卷