§3.3 Carnot定理 Th 高温热源 W=W lo' W W W 71= 2 门R R 一W 21 e'w 1o-w 假设 W W n>ng T。低温热源 2, 21 (a) 2>21 所有量取绝对值
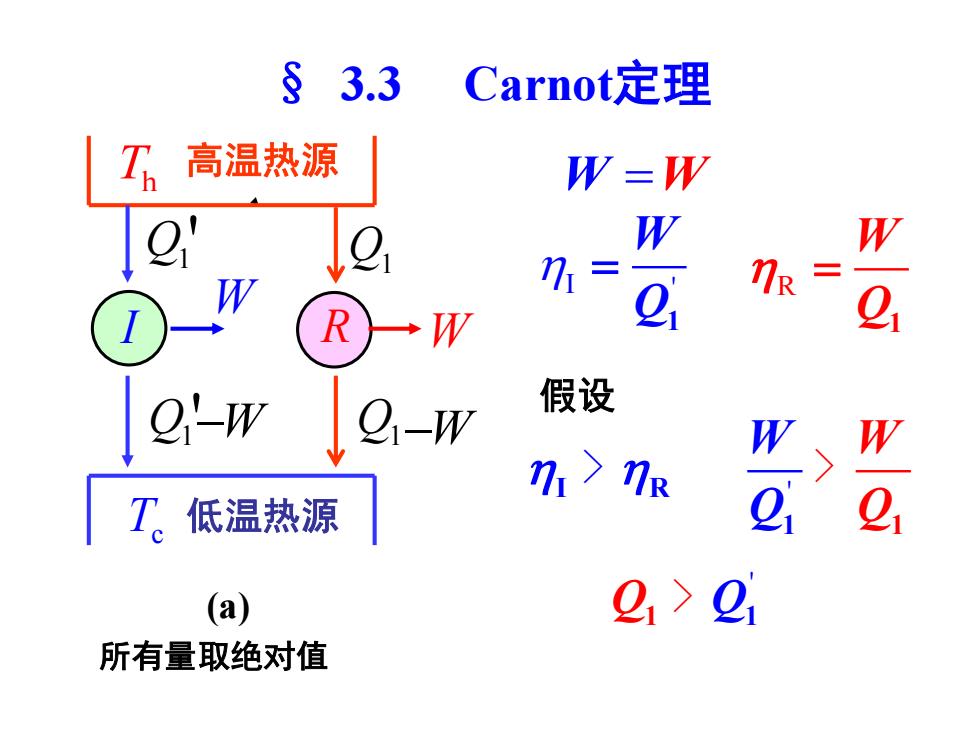
§ 3.3 Carnot定理 Th 高温热源 Tc 低温热源 Q1 W Q1 ' W Q1 '−W Q1−W I R (a) W =W I ' W Q = 1 R W Q = 1 假设 I R > ' W Q W 1 Q1 > ' Q1 Q1 > 所有量取绝对值
§2.3 Carnot定理 Th 高温热源 从低温热源吸热 (2-W)-(2-W) wW R =(2-2)>0 -W e-w 高温热源得到热 T。低温热源 (2-2) 这违反了Clausius说法,只有 (b) 1≤7R
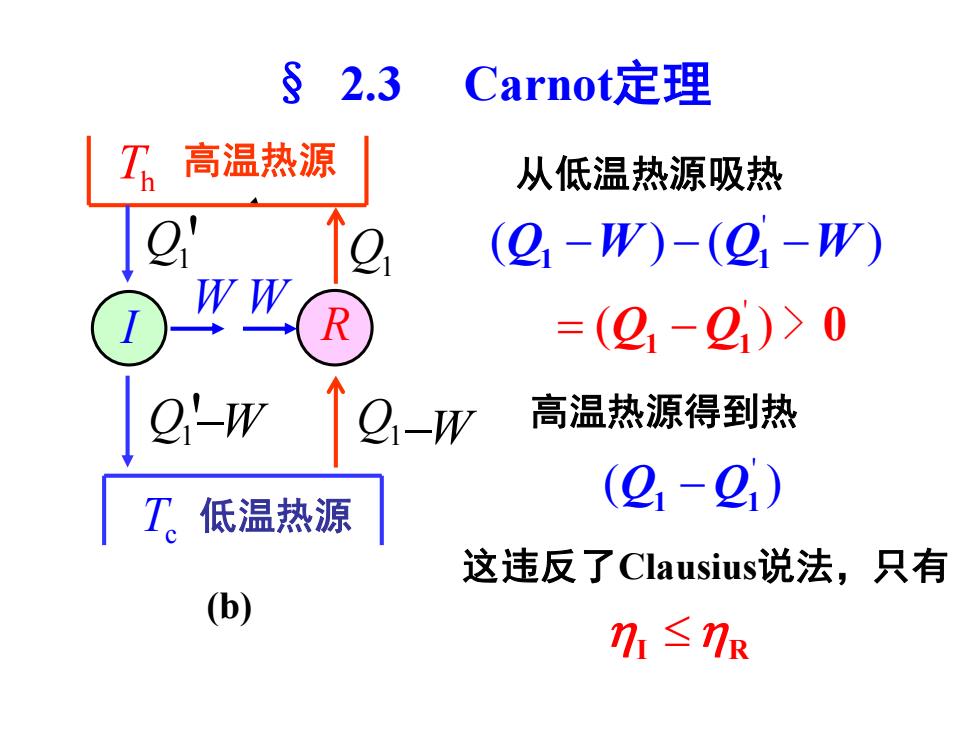
§ 2.3 Carnot定理 Th 高温热源 Tc 低温热源 Q1 W Q1 ' W Q1 '−W Q1−W I R (b) ' ( ) ( ) Q W Q W 1 1 − − − ' = − ( ) Q Q 1 1 > 0 从低温热源吸热 I R 高温热源得到热 ' ( ) Q Q 1 1 − 这违反了Clausius说法,只有

§3.3 Carnot定理 Carnot定理推论: 所有工作于同温热源与同温冷源之间的可逆热机, 其热机效率都相等,即与热机的工作物质无关。 Carnot定理的意义: (1)引入了一个不等号:≤,原则上解决了 化学反应的方向问题; (2)原则上解决了热机效率的极限值问题
Carnot定理推论: Carnot定理的意义: (2)原则上解决了热机效率的极限值问题。 (1)引入了一个不等号 ,原则上解决了 化学反应的方向问题; I R § 3.3 Carnot定理 所有工作于同温热源与同温冷源之间的可逆热机, 其热机效率都相等,即与热机的工作物质无关

§3.4熵的概念 从Carnot循环得到的结论: 即Carnot循环中,热效应与温度商值的加和等于零。 =0 T T 对于任意的可逆循环,都可以分解为若干个 小Carnot循环
§3.4 熵的概念 从Carnot循环得到的结论: Q Q T T + = c h c h 0 对于任意的可逆循环,都可以分解为若干个 小Carnot循环。 即Carnot循环中,热效应与温度商值的加和等于零

任意可逆循环的热温商 任意可逆循环热温商的加和等于零,即: 证明如下:()在如图所示的任意可逆 M 循环的曲线上取很靠近的PQ过程; 图2.3任意可逆循环 (2)通过P,Q点分别作RS和TU两条可逆绝热膨胀线, (3)在P,Q之间通过O点作等温可逆膨胀线VW,使两 个三角形PVO和OWQ的面积相等, 这样使PO过程与PYOWO过程所作的功相同。 同理,对MW过程作相同处理,使MXO'YN折线所经过 程作功与MN过程相同。WX就构成了一个卡诺循环
R ( ) 0 i i i Q T = 任意可逆循环的热温商 证明如下: 任意可逆循环热温商的加和等于零,即: 同理,对MN过程作相同处理,使MXO’YN折线所经过 程作功与MN过程相同。VWYX就构成了一个卡诺循环。 或 (2)通过P,Q点分别作RS和TU两条可逆绝热膨胀线, (1)在如图所示的任意可逆 循环的曲线上取很靠近的PQ过程; (3)在P,Q之间通过O点作等温可逆膨胀线VW,使两 个三角形PVO和OWQ的面积相等, 这样使PQ过程与PVOWQ过程所作的功相同。 0 δ R = T Q