
2.2自动控制系统数学模型 2.2.2解析法建模 1.响应曲线法主要用于测取阶跃响应曲线 图2.8响应曲线 (a)阶跃响应曲线:(b)矩形脉冲响应曲线 第2章自动控制系统基本知识 6
第2章 自动控制系统基本知识 6 2.2.2 解析法建模 2.2 自动控制系统数学模型 1.响应曲线法 主要用于测取阶跃响应曲线

2.2自动控制系统数学模型 2.2.2解析法建模 2.矩形脉冲响应曲线法 采用矩形脉冲作为输入信号, 0 施加在对象的输入端,同时记 录输出端跟随时间变化的特性 曲线。 240 3to 410 图2.9矩形脉冲响应曲线转换为阶跃响应曲线 第2章自动控制系统基本知识
第2章 自动控制系统基本知识 7 2.2 自动控制系统数学模型 2.2.2 解析法建模 2.矩形脉冲响应曲线法 采用矩形脉冲作为输入信号, 施加在对象的输入端,同时记 录输出端跟随时间变化的特性 曲线

2.2自动控制系统数学模型 2.2.2解析法建模 3.由阶跃响应曲线建立对象数学模型 一阶特性 0,(S)= Ko Tos+1 亦可用此函数描述: ,6)= -e-rs 0(S)= Tos+1 0(S)= Ts(Ts+1) n阶特性 0()= K。 (Tos+1)” Ko () e 第2章自动控制系统基本知识 8
第2章 自动控制系统基本知识 8 2.2.2 解析法建模 3.由阶跃响应曲线建立对象数学模型 2.2 自动控制系统数学模型 0 0 0 ( ) 1 = + K s T s 0 0 0 ( ) 1 − = + K s s e T s 0 0 0 ( ) ( 1) = + n K s T s 0 0 0 ( ) ( 1) − = + s n K s e T s 0 1 ( ) − = s a s e T s 0 1 2 1 ( ) ( 1) − = + s s e T s T s 一阶特性 n阶特性 亦可用此函数描述:
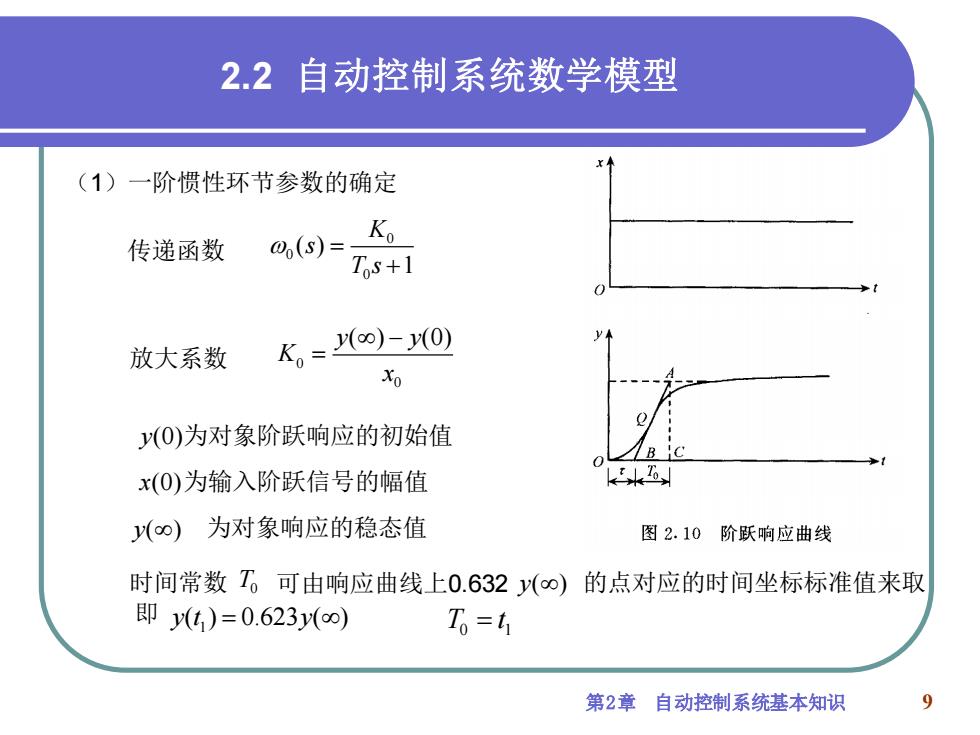
2.2自动控制系统数学模型 (1)一阶惯性环节参数的确定 传递函数 0(S)= Ko Tos+1 放大系数 K。=o)-y0) Xo y(O)为对象阶跃响应的初始值 x(O)为输入阶跃信号的幅值 (o)为对象响应的稳态值 图2.10阶跃响应曲线 时间常数T,可由响应曲线上0.632y(o) 的点对应的时间坐标标准值来取 即yt)=0.623(∞) To=t 第2章自动控制系统基本知识
第2章 自动控制系统基本知识 9 (1)一阶惯性环节参数的确定 0 0 0 ( ) 1 = + K s T s 0 0 ( ) (0) − = y y K x T t 0 1 = 2.2 自动控制系统数学模型 传递函数 放大系数 y( ) y(0) x(0) 为对象阶跃响应的初始值 为对象响应的稳态值 为输入阶跃信号的幅值 时间常数 T0 可由响应曲线上0.632 y( ) 的点对应的时间坐标标准值来取 即 1 y t y ( ) 0.623 ( ) =
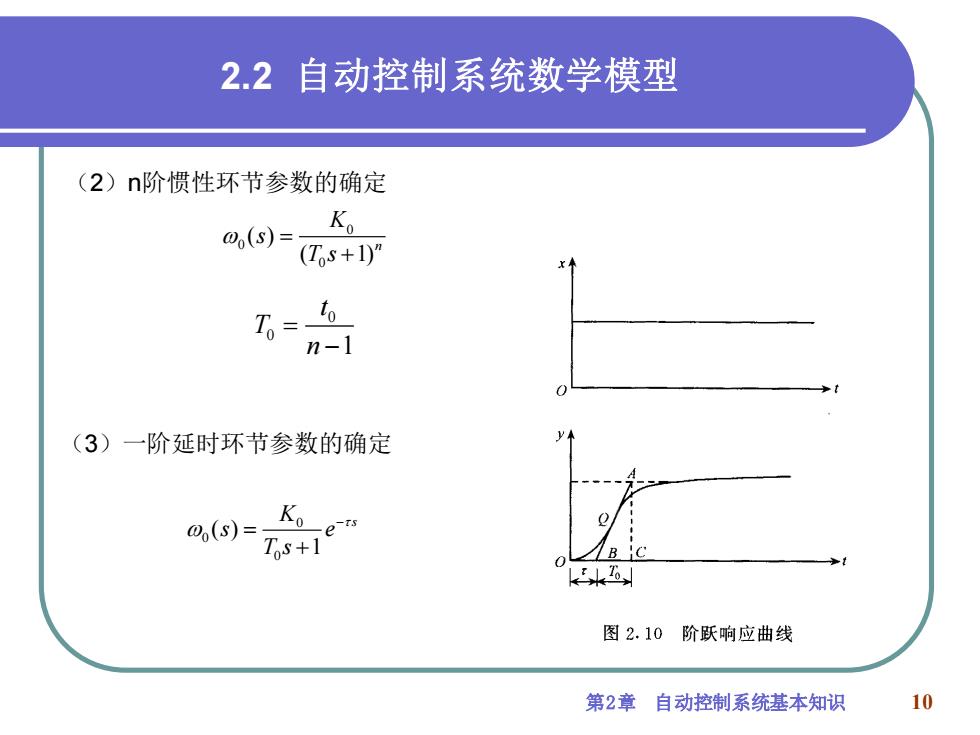
2.2自动控制系统数学模型 (2)n阶惯性环节参数的确定 0(S)= K (Ts+1)” n-1 (3)一阶延时环节参数的确定 0(S)= Ko er Tos+ B C 图2.10阶跃响应曲线 第2章自动控制系统基本知识 10
第2章 自动控制系统基本知识 10 (2)n阶惯性环节参数的确定 0 0 0 ( ) ( 1) = + n K s T s 0 0 1 = − t T n (3)一阶延时环节参数的确定 0 0 0 ( ) 1 − = + K s s e T s 2.2 自动控制系统数学模型