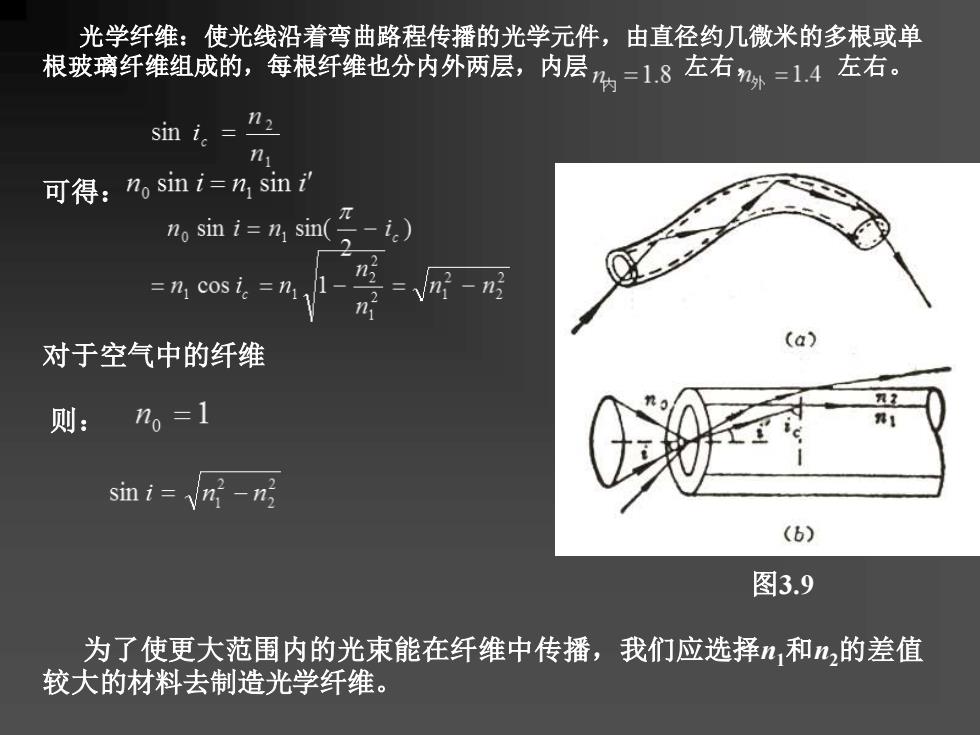
光学纤维:使光线沿着弯曲路程传播的光学元件,由直径约几微米的多根或单 根玻璃纤维组成的,每根纤维也分内外两层,内层内=1.8左右外=1.4左右。 sin i2 n 可得:no sin i=n1sini no(-i) =n1c0s.=n11- (a) 对于空气中的纤维 n? 则: n=1 sin i=n-n (b) 图3.9 为了使更大范围内的光束能在纤维中传播,我们应选择n,和n,的差值 较大的材料去制造光学纤维
光学纤维:使光线沿着弯曲路程传播的光学元件,由直径约几微米的多根或单 根玻璃纤维组成的,每根纤维也分内外两层,内层 左右, 左右。 可得: 对于空气中的纤维 则: 图3.9 为了使更大范围内的光束能在纤维中传播,我们应选择n1和n2的差值 较大的材料去制造光学纤维

四、棱镜 出射线和入射线之间的交角日称为偏向角 0=(-i2)+(-) 又因 0=i,+-A 可以证明:当,=时偏向角达最小值。 最小偏向角9。=2i1-A i1= 0。+A 又当:i=时,折射角为 =2= A sin 0。+A 图3.10 sini 2 1n= sini A sin
四、棱镜 出射线和入射线之间的交角 称为偏向角 又因 可以证明:当 时偏向角达最小值。 最小偏向角: 又当: 时,折射角为 图3.10 i 2 + i 2 = A 2 0 1 A i + = 1 1 i = i 2 2 2 A i = i =

第五节光在球面上的反射和折射 单独一个球面不仅是一个简单的光学系统,而且是组成 光学仪器的基本元件,研究光经由球面的反射和折射,是 一般光学系统成象的基础。 一、符号法则 为了研究光线经由球面反射和折射的光路,必须先说明 一些概念以及规定一些适当的符号法则,以便使所得的结 果能普遍适用。 球面的中心点O称为顶点,球面的球心C称为曲率中心, 球面的半径称为曲率半径。CO称为主轴,通过主轴的平面 称为主截面。主轴对于所有的主截面具有对称性。因而我 们只须讨论一个主截面内光线的反射
第五节 光在球面上的反射和折射 单独一个球面不仅是一个简单的光学系统,而且是组成 光学仪器的基本元件,研究光经由球面的反射和折射,是 一般光学系统成象的基础。 一、符号法则 为了研究光线经由球面反射和折射的光路,必须先说明 一些概念以及规定一些适当的符号法则,以便使所得的结 果能普遍适用。 球面的中心点O称为顶点,球面的球心C称为曲率中心, 球面的半径称为曲率半径。CO称为主轴,通过主轴的平面 称为主截面。主轴对于所有的主截面具有对称性。因而我 们只须讨论一个主截面内光线的反射

在计算任一条光线的线段长度和角度时,我们对符号作如下规定。 (1)光线和主轴交点的位置都从顶点算起,凡在顶点右方者,其间距离 的数值为正;凡在顶点左方者,其间距离的数值为负。物点或象点至主轴 的距离,在主轴上方为正,在下方为负。 (2)光线方向的倾斜角度都从主轴(或球面法线)算起,并取小于的 角度,由主轴(或球面法线)转向有关光线时,若沿顺时针方向转,则该 角度的数值为正;若沿逆时针方向转动时的,则该角度的数值为负。 (3)在图中出现的长度和角度只用正值。假定光线自左向右进行。 图3.11
在计算任一条光线的线段长度和角度时,我们对符号作如下规定。 (1)光线和主轴交点的位置都从顶点算起,凡在顶点右方者,其间距离 的数值为正;凡在顶点左方者,其间距离的数值为负。物点或象点至主轴 的距离,在主轴上方为正,在下方为负。 (2)光线方向的倾斜角度都从主轴(或球面法线)算起,并取小于 的 角度,由主轴(或球面法线)转向有关光线时,若沿顺时针方向转,则该 角度的数值为正;若沿逆时针方向转动时的,则该角度的数值为负。 (3)在图中出现的长度和角度只用正值。假定光线自左向右进行。 图3.11

二、球面反射对光束单心性的破坏 光线△MC的光程为:(PAP )=nl+nl 在PAP和APAC中应用余弦定理, PC=(-S)-(-r)=r-s CP'=-r-(-S)=S'-I I=-r)2+(r-s)2+2-rXr-s)coso] 1'=-[【-r2+('-r)2-2(-rs'-r)cosp月 图3.12 根据费马原理,指定两点间(是否更为确切)光程应取稳定值。 则: 2tm小wm。片片 do 11s'-r1 或: r-s s'-r =0 +ic-7 显然,S'的值随u亦即角p的变化而变化,亦即从物点发散的单心光束经球面反 射后,将不在保持单心(即使平行入射也不例外),这一点可用3.10图说明
二、球面反射对光束单心性的破坏 光线 的光程为: 在 和 中应用余弦定理, 图3.12 根据费马原理,指定两点间(是否更为确切)光程应取稳定值。 则: 或: 显然, 的值随u亦即角 的变化而变化,亦即从物点发散的单心光束经球面反 射后,将不在保持单心(即使平行入射也不例外),这一点可用3.10图说明。 PAP (PAP) = nl + nl PAC ACP 2 1 2 2 2 1 2 2 ( ) ( ) 2( )( ) cos ( ) ( ) 2( )( ) cos ( ) ( ) ( ) l r s r r s r l r r s r r s CP r s s r PC s r r s = − + − − − − = − + − + − − = − − − = − = − − − = − l r s l s r l l l s r l r s + − − + = = − − − 1 ( ) 1 1 0 ( ) 1 1 1 l s l s l l r + + =