
北京化二大学 第三节 单螺杆挤出理论 化简后,x、y、方向的运动方程 OP 十 Ty二 0 (1) az dy OP 0tyx二0 (2) OX dy OP :0 (3) dy
= 0 ∂ ∂ + ∂ ∂ − yZ P yz τ = 0 ∂ ∂ + ∂ ∂ − yX P yx τ = 0 ∂ ∂ − y P (1) (2) (3) 化简后,x、y、z方向的运动方程 方向的运动方程 第三节 单螺杆挤出理论 单螺杆挤出理论

北京化二大学 第三节 单螺杆挤出理论 本构方程: Tyx =7 OV (4) dy av, 7 (5) dy
y Vx yx ∂ ∂ = ητ y Vz yz ∂ ∂ = ητ 本构方程: (5) (4) 第三节 单螺杆挤出理论 单螺杆挤出理论

北京化二大学 第三节 单螺杆挤出理论 四、熔体输送理论 (一)牛顿流体的理论模型 2、速度分布方程及流量 (1)Z向的速度分布方程及流量 a、Z向的速度分布方程 Op 0'V 将(5)式代入(1)式: +7 =0 Oz ⊙y2 积分一次得: ,1.ap dy y+c1
2、速度分布方程及流量 、速度分布方程及流量 (1)Z向的速度分布方程及流量 向的速度分布方程及流量 a、Z向的速度分布方程 向的速度分布方程 0 2 2 = ∂ ∂ + ∂ ∂ − y V z P z η 积分一次得: 将(5)式代入(1)式: 第三节 单螺杆挤出理论 单螺杆挤出理论 四、熔体输送理论 四、熔体输送理论 (一)牛顿流体的理论模型 (一)牛顿流体的理论模型

北京化二大学 第三节 单螺杆挤出理论 四、熔体输送理论 二次积分得: +Cy+C 0z2 积分常数C和C2可由以下边界条件求得: y=0,Vz=0→C2=0; y=h3,Vz=Vbz→ Vo_ h OP C1= h270z
二次积分得: 积分常数C1和C2可由以下边界条件求得: 可由以下边界条件求得: y=0,Vz=0→c2=0; y=h3,Vz=Vbz→ 3 1 3 2 Vbz h P c h z η ∂ = − ∂ 四、熔体输送理论 四、熔体输送理论 第三节 单螺杆挤出理论 单螺杆挤出理论 2 1 2 1 2 z P y V C y C η z ∂ = + + ∂ ii i
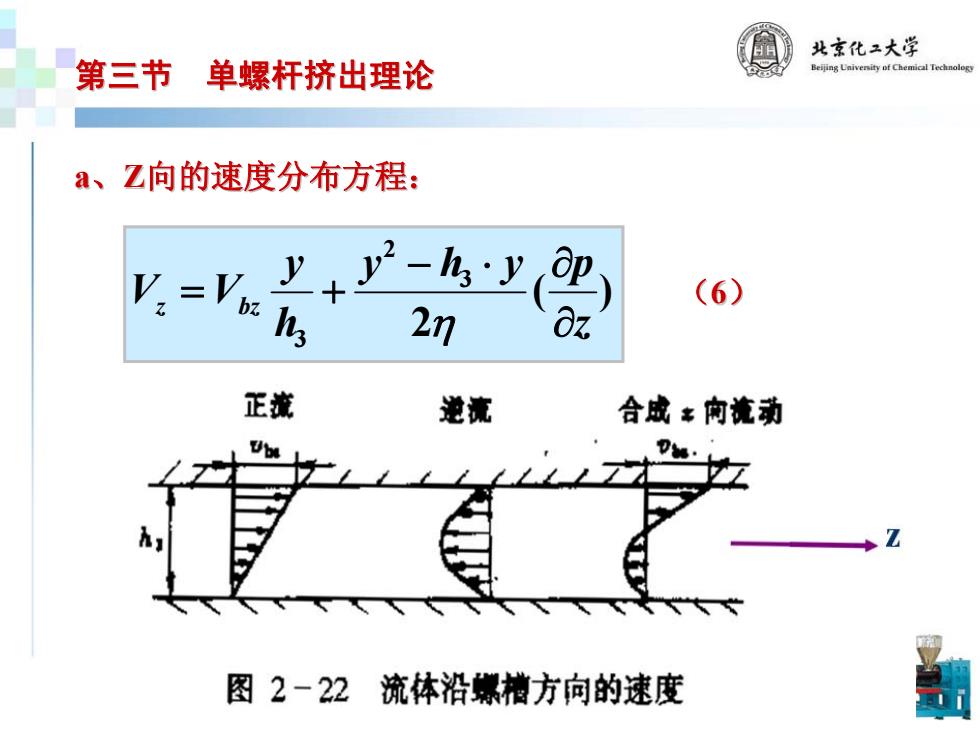
北京化二大学 第三节 单螺杆挤出理论 a、Z向的速度分布方程: V:=Vht -y迎 (6) h 2n Oz 正藏 逆流 合成多向流动 图2-22 流体沿爆槽方向的速度
a、Z向的速度分布方程: 向的速度分布方程: )( (6) 2 3 2 3 z pyhy h y VV bzz ∂∂⋅− += η 第三节 单螺杆挤出理论 单螺杆挤出理论