
北京化二大学 第三节 单螺杆挤出理论 b、z方向流体的体积流率一Q 体积流率Q=Vz×螺槽横截面 Qz Wif"Vzdy iv Whs iwh (7) 2 1211 第一项:正流流量 第二项:逆流流量
b、z方向流体的体积流率- 方向流体的体积流率-Q 体积流率Q=Vz× 螺槽横截面 第一项:正流流量 第一项:正流流量 第二项:逆流流量 第二项:逆流流量 (7) )( 122 1 3 3 3 0 3 Z WhiV PiWh dyVWiQ bz h Z Z ∂ ∂ = − = ∫ η 第三节 单螺杆挤出理论 单螺杆挤出理论

北京化二大学 第三节 单螺杆挤出理论 '=πD ncosp W=πD sing-e'≈πD sino ap aP △P d sino= sinp,,k= &z OL L sino 将上式代入(7)式: 元2.D2.n.h·sinp.cos_元.D.sin2p,oP 2 12n1 aL =Qd+Cp
, 3 cos W D sin -e D sin sin sin , sin V Dn bz PP P dL dz zL L π ϕ π ϕπ ϕ ϕ ϕ ϕ = = ≈ ∂∂ Δ = =⋅ = ∂ ∂ ∵ 将上式代入(7)式: Pd 1 23 3 3 22 Q 12 sin 2 cossin Q L hnD hD P Q += ∂ ∂ ⋅ ⋅⋅⋅ − ⋅⋅⋅⋅⋅ = η π πϕϕ ϕ 第三节 单螺杆挤出理论 单螺杆挤出理论

北京化二大学 第三节 单螺杆挤出理论 (2)沿x方向流体的速度分布及流量 a、x方向的速度分布方程 ap o'v 将(4)代入(2),得: 7 Ox 积分(边界条件:y=0,Vx=0;y=h3’Vx=-Vbx) (9) 2n1
(2)沿x方向流体的速度分布及流量 方向流体的速度分布及流量 a、x方向的速度分布方程 方向的速度分布方程 将(4)代入(2),得: 积分(边界条件: 积分(边界条件:y=0, Vx=0;y=h3,Vx= -Vbx) )( 2 13 2 3 x pyhy h y x VV bx ∂∂⋅− +−= η (9) 第三节 单螺杆挤出理论 单螺杆挤出理论 2 2 P Vx x y η ∂ ∂ = ∂ ∂

北京化二大学 第三节 单螺杆挤出理论 b、Qx(在x方向上的单宽流率) h 1 Q= V.dy=-Yah 2 ;=0 12m10x 在x方向上料流的压力梯度: Op -6n1 (10) Ox 居 (10)代入(9): V.-Vy 2-3y (11) ;
b、Qx (在x方向上的单宽流率) 方向上的单宽流率) 在x方向上料流的压力梯度: 方向上料流的压力梯度: 0h x P 12η 1 h 2 V dyVQ 3 1 3 bx x h 0 x 3 = ∂ ∂ −−== ∫ (10) (10)代入(9): (11) 2 3 6 1 hV xP bx −= η ∂∂ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ bx x 3 3 y y = 2-3 V V h h 第三节 单螺杆挤出理论 单螺杆挤出理论
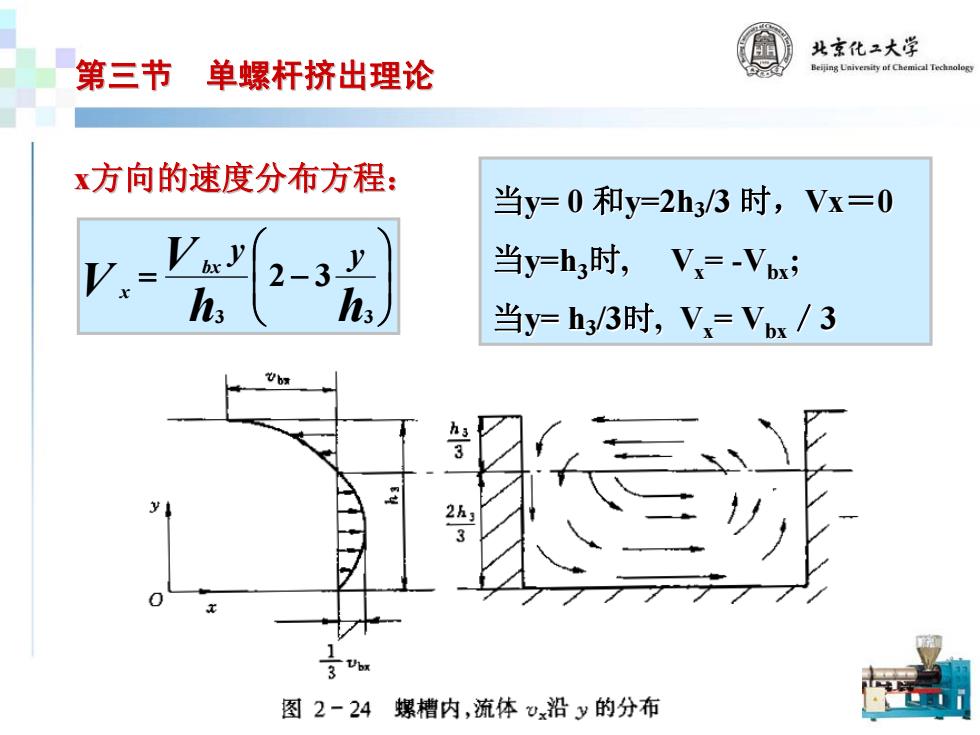
北京化二大学 第三节 单螺杆挤出理论 x方向的速度分布方程: 当y=0和y=2h3/3时,Vx=0 V-Vay 2-3业 当y=h3时,Vx=Vbx; h 当y=h/3时,V=Vbx/3 零 图2-24螺槽内,流体0沿y的分布
x方向的速度分布方程: 方向的速度分布方程: 当y= 0 和y=2h3/3 时,Vx=0 0 当y=h3时, Vx= -Vbx; 当y= h3/3时, Vx= Vbx/3 ⎟⎟⎠⎞ ⎜⎜⎝⎛ = − hhV V y y bx x 3 3 32 第三节 单螺杆挤出理论 单螺杆挤出理论