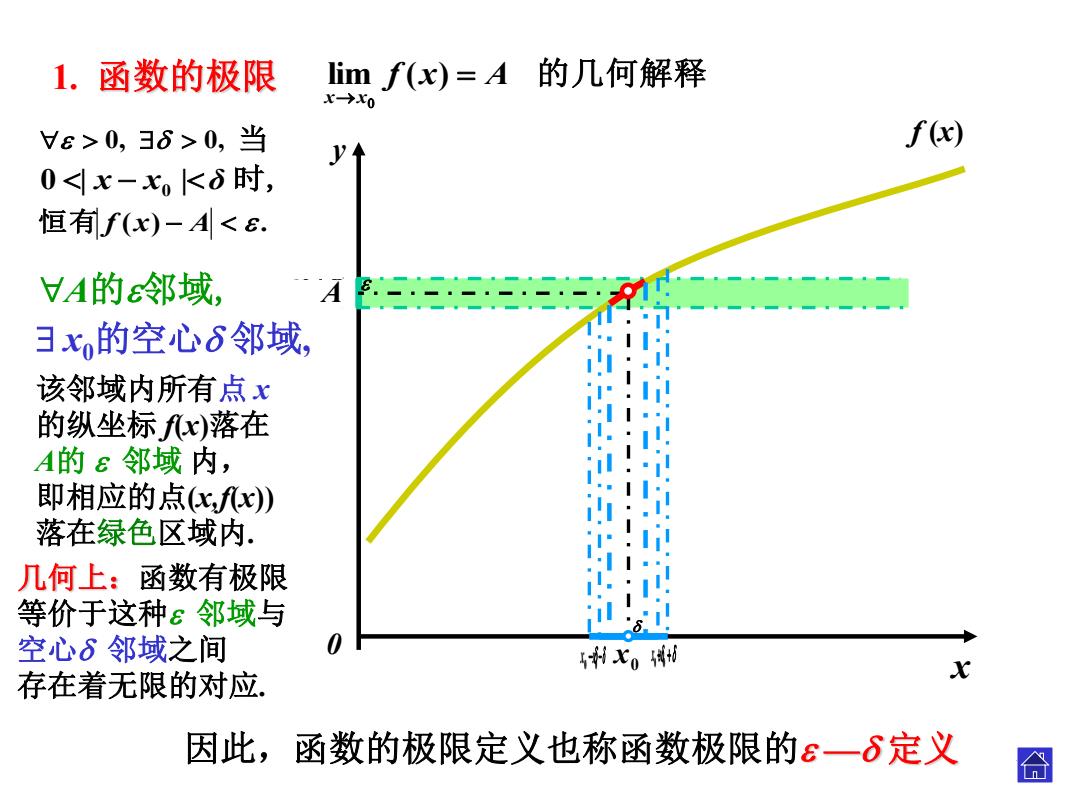
1.函数的极限 limf(x)=A的几何解释 x→x0 Vε>0,36>0,当 f(x) y 0<x-xK6时, 恒有f(x)-A<E. VA的邻域, A 3x的空心6邻域, 该邻域内所有点x 的纵坐标fx)落在 A的ε邻域内, 即相应的点(c,x) 落在绿色区域内. 几何上:函数有极限 等价于这种ε邻域与 空心δ邻域之间 0 利七o博0 存在着无限的对应 X 因此,函数的极限定义也称函数极限的ε一δ定义
A x y 0 0 x A A 0 x 0 x 0 x 0 x 几何上:函数有极限 等价于这种 邻域与 空心 邻域之间 存在着无限的对应. 1. 函数的极限 lim f (x) A 的几何解释 x x 因此,函数的极限定义也称函数极限的 — 定义 . f (x) 该邻域内所有点 x 的纵坐标 f(x)落在 A的 邻域 内, 即相应的点(x,f(x)) 落在绿色区域内. A的邻域, x0的空心 邻域, 恒有 f (x) A . 0, 0, 当 0 | x x0 |δ 时
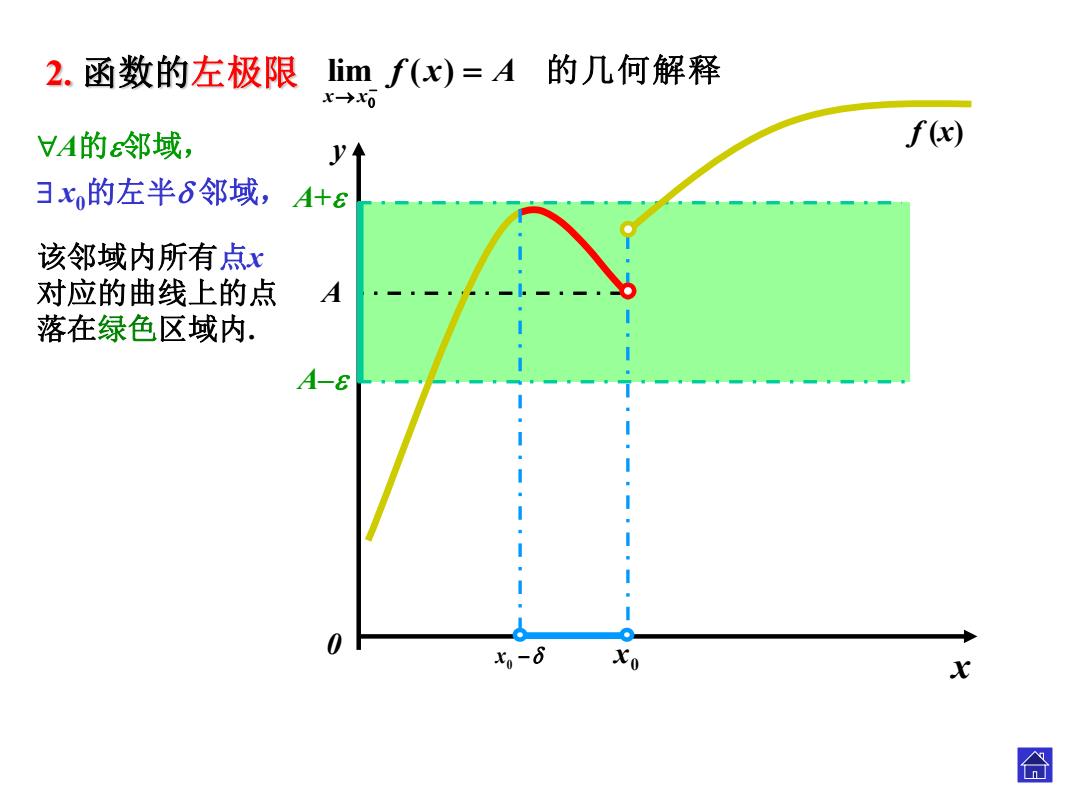
2.函数的左极限 Iimf(x)=A的几何解释 VA的s邻域, f(x) y 彐x的左半6邻域,A+e 该邻域内所有点x 对应的曲线上的点 A 落在绿色区域内. A-8 七,-8 xo X 合
x y0 f (x ) 0 x A 0 x 该邻域内所有 点 x 对应的曲线上的点 落在绿色区域内 . 2. 函数的左极限 lim f ( x ) A 的几何解释 x x A的 邻域, x0的左半 邻域, A + A –

2.函数的左极限 limf(x)=A的几何解释 VA的s邻域, f(x) y x的左半6邻域,A+8 该邻域内所有点x 对应的曲线上的点 A 落在绿色区域内. A-8 七,-8 xo X 合
A x y 0 f (x) 0 x A A 0 x lim f (x) A 的几何解释 x x 2. 函数的左极限 . 该邻域内所有点x 对应的曲线上的点 落在绿色区域内. A的邻域, x0的左半 邻域

2.函数的左极限 limf(x)=A的几何解释 x→X0 VA的邻域, f(x) y 3x的左半6邻域, 4t8 该邻域内所有点x A 对应的曲线上的点 A 落在绿色区域内. 七,-6 xo X 合
A x y 0 f (x) 0 x0 x A A A A A A A A lim f (x) A 的几何解释 x x 2. 函数的左极限 . 该邻域内所有点x 对应的曲线上的点 落在绿色区域内. A的邻域, x0的左半 邻域

2.函数的左极限 limf(x)=A的几何解释 VA的邻域, y f(x) 3x的左半6邻域, 该邻域内所有点x A+6 对应的曲线上的点 A 落在绿色区域内. A-8 七。-8 X 合
A x y 0 f (x) 0 x A A 0 x 2. 函数的左极限 lim f (x) A 的几何解释 x x . 该邻域内所有点x 对应的曲线上的点 落在绿色区域内. A的邻域, x0的左半 邻域