
熵的概念 •从卡诺循环得到的结论 •任意可逆循环的热温商 熵的引出 •熵的定义
熵的概念 Xi’an University of science & Technology •从卡诺循环得到的结论 •任意可逆循环的热温商 •熵的引出 •熵的定义

从卡诺循环得到的结论 nology -W 2+2 Th-Te 7= C 9. T 1+ =1- 2. T To T 或: T 即卡诺循环中,热效应与温度商值的加和等于零
从卡诺循环得到的结论 Xi’an University of science & Technology h c h c h h h W Q Q T T Q Q T − + − = = = h c h c 1 1 T T Q Q + = − h h c c T Q T Q = − c h c h 0 Q Q T T + = 或: 即卡诺循环中,热效应与温度商值的加和等于零
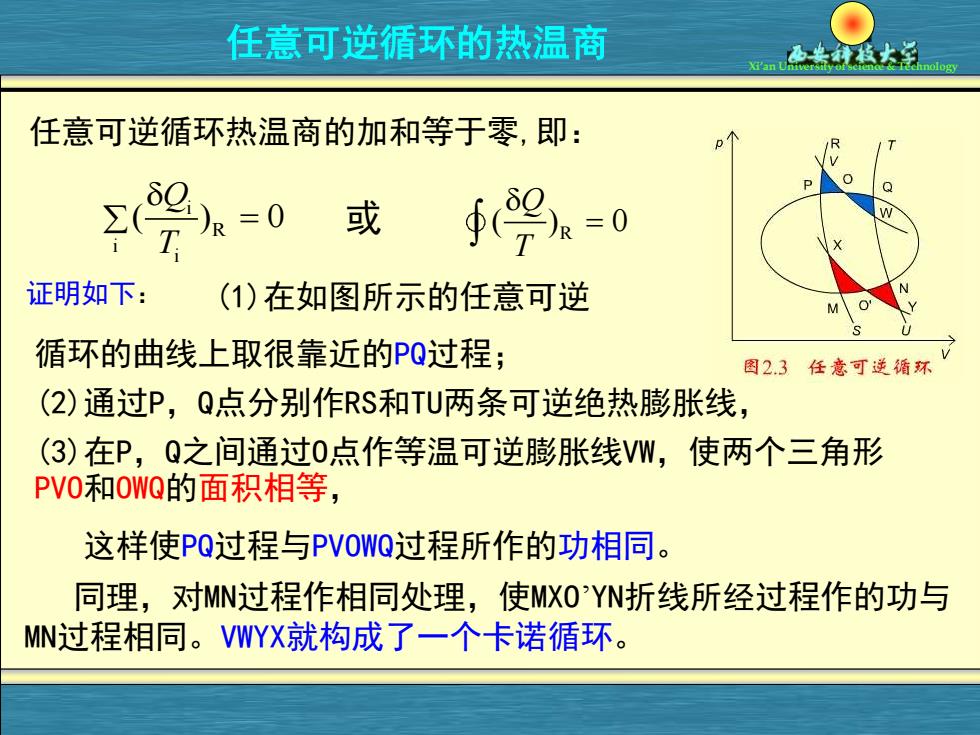
任意可逆循环的热温商 任意可逆循环热温商的加和等于零,即: R 证明如下: (1)在如图所示的任意可逆 M 循环的曲线上取很靠近的PQ过程; 图2.3任意可逆循环 (2)通过P,Q点分别作RS和TU两条可逆绝热膨胀线, (3)在P,Q之间通过0点作等温可逆膨胀线VW,使两个三角形 PV0和OWQ的面积相等, 这样使PQ过程与PVOWQ过程所作的功相同。 同理,对MN过程作相同处理,使MXO'YN折线所经过程作的功与 MN过程相同。VWYX就构成了一个卡诺循环
Xi’an University of science & Technology i R i i ( ) 0 Q T = 任意可逆循环的热温商 证明如下: 任意可逆循环热温商的加和等于零,即: 同理,对MN过程作相同处理,使MXO’YN折线所经过程作的功与 MN过程相同。VWYX就构成了一个卡诺循环。 R ( ) 0 Q T = 或 (2)通过P,Q点分别作RS和TU两条可逆绝热膨胀线, (1)在如图所示的任意可逆 循环的曲线上取很靠近的PQ过程; (3)在P,Q之间通过O点作等温可逆膨胀线VW,使两个三角形 PVO和OWQ的面积相等, 这样使PQ过程与PVOWQ过程所作的功相同
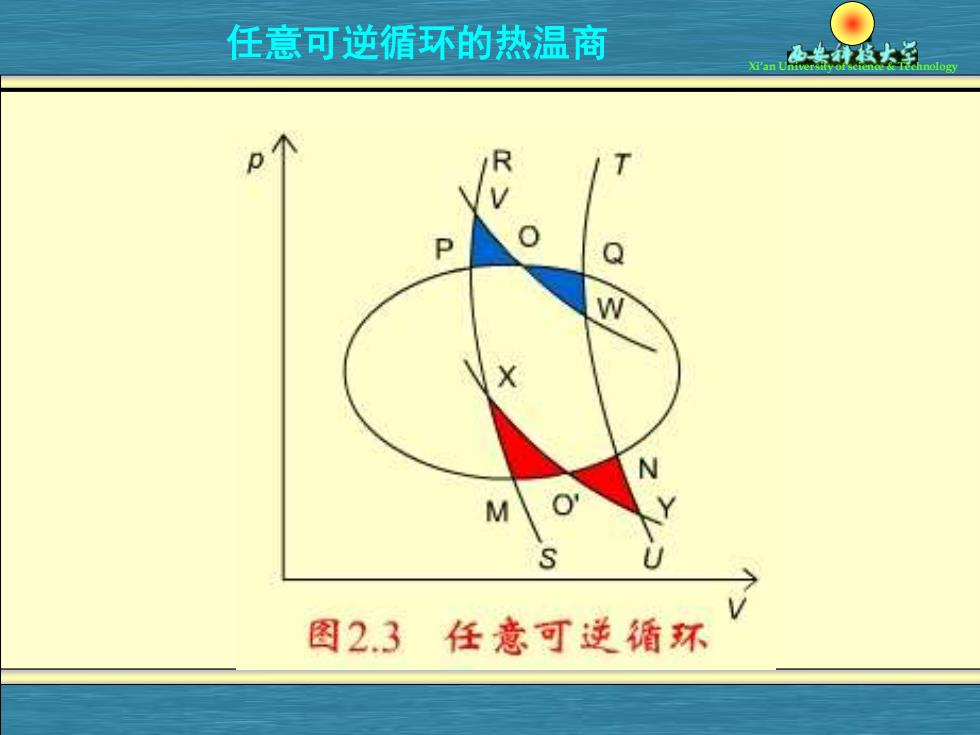
任意可逆循环的热温商 nology M 图2.3任意可逆循环
任意可逆循环的热温商 Xi’an University of science & Technology

任意可逆循环的热温商 用相同的方法把任意可逆 循环分成许多首尾连接的小卡 诺循环,前一个循环的等温可 逆膨胀线就是下一个循环的绝 热可逆压缩线,如图所示的虚 线部分,这样两个过程的功恰 好抵消。 图2.4一连串卡诺循环 从而使众多小卡诺循环的总效应与任意可逆循 环的封闭曲线相当,所以任意可逆循环的热温商的 加和等于零,或它的环程积分等于零
任意可逆循环的热温商 Xi’an University of science & Technology 用相同的方法把任意可逆 循环分成许多首尾连接的小卡 诺循环,前一个循环的等温可 逆膨胀线就是下一个循环的绝 热可逆压缩线,如图所示的虚 线部分,这样两个过程的功恰 好抵消。 从而使众多小卡诺循环的总效应与任意可逆循 环的封闭曲线相当,所以任意可逆循环的热温商的 加和等于零,或它的环程积分等于零