
章离心泵的基本方程 第二节基本方程 欧拉方程 动量矩定律:质点系对某一轴线的动量矩的时间 变化率等于作用于该质点系上的所有外力矩。 dt内,质点系1221动量矩的变化 △L=L(1’2’2’1’)-L(1221) =L(22’2’2)-L(11’1’1)2?4 =dm2 C2u r2 dmi Ciu ri dm(C2u r2-Ciu r1) 外力矩 M=pQr(c2ur2-C1ur) 叶轮对流体作的功 N=MO=P QT (C2u U2-Ciu u1) 叶轮对单位重量流体作功 Hr∞=(c2uu2-C1uu1)/g
第 2 章 离心泵的基本方程 第二节 基本方程 动量矩定律:质点系对某一轴线的动量矩的时间 变化率等于作用于该质点系上的所有外力矩。 1 1 1’ 1’ 2’ 2’ 2 2 R2 R1 △L= L(1’2’2’1’ )-L(1221) = L(22’2’2 )-L(11’1’1) =dm2 c2u r2 – dm1 c1u r1 = dm(c2u r2 – c1u r1) 欧拉方程 dt内,质点系1221动量矩的变化 外力矩 叶轮对流体作的功 叶轮对单位重量流体作功 M=ρQT(c2u r2 – c1u r1) N=Mω=ρQT(c2u u2 – c1u u1) HT∞ =(c2u u2 – c1u u1)/g

章离心泵的基本方程 w9 第二节基本方程 理论扬程盟T一的影响因素 C10≈0 Hr∞=(C2u∞u2-C1u∞ui)/g 60 C2u=u2-C2mctgB2A nπD2Qr 60b2t2 60 -ctgβ2A πd,b2t2 B2A>908 D2 D2 B24=90° D D2' B2A<90° D2” D2" Q Qy
第 2 章 离心泵的基本方程 第二节 基本方程 理论扬程HT∞的影响因素 c1u∞ ≈ 0 60 2 2 n D u π = A T u r A ctg d b n D Q c u c ctg 2 2 2 2 2 2 2 2 2 60 β π τ π β = − ∞ = − ∞ ] 60 ) 60 [( 1 2 2 2 2 2 A T T ctg b n D Q n g H β τ π ⋅ ∞ = − HT∞ =(c2u∞ u2 – c1u∞ u1)/g β2A <90° β2A =90° H β2A >90° T∞ QT D2 ′ HT∞ QT D2 ″ D2 D2 D2 ′ D2 ″

章离心泵的基本方程 第二节基本方程 理论扬程H的影响因素 H。=1[nD)2- g 60 Or'n ciglβ2J 60b2t2 B2A 2A” 82A 2A n n
β2A ′ HT∞ QT β2A ″ β2A b2 ′ HT∞ QT b2 ″ b2 第 2 章 离心泵的基本方程 第二节 基本方程 理论扬程HT∞的影响因素 τ2 ′ HT∞ QT τ2 ″ τ2 n2 ′ HT∞ QT n2 ″ n2 ] 60 ) 60 [( 1 2 2 2 2 2 A T T ctg b n D Q n g H β τ π ⋅ ∞ = − β2A ′ β2A β2A ″ n′ n n″ b2 ′ b2 b2 ″
第 章离心泵的基本方程 第三节反作用度 反作用度 Win =c+-2.uCxm cosa2 c+-2.42"Ca cm4=(c3n+G-1wn)/2,1m4=(G2+4-w)/2 H∞=(C2u∞u2-C1u∞u1/g 欧拉第二方程 动能头H。 静能头H C2 定义:单位重量流体流经叶 28 28 轮后静压能的增量H。与理 论能头H之比.p=H,/Hr
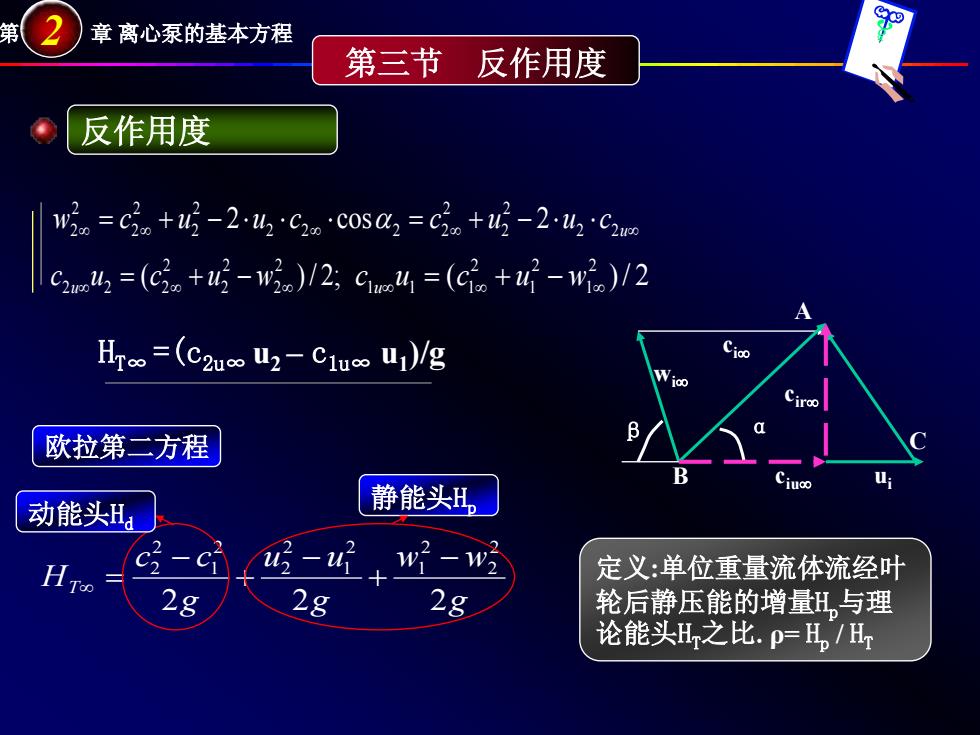
第 2 章 离心泵的基本方程 ∞ ∞ ∞ ∞ ∞ = + − ⋅ ⋅ ⋅ = + − ⋅ ⋅ u w c u u c c u u c 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 cosα 2 ( )/ 2; 2 2 2 2 2 2 ∞ 2 = 2∞ + − w ∞ c u c u u g w w g u u g c c HT 2 2 2 2 2 2 1 2 1 2 2 2 1 2 2 − + − + − ∞ = 欧拉第二方程 ui wi∞ ci∞ β α ciu∞ cir∞ A B C 第三节 反作用度 反作用度 ( )/ 2 2 1 2 1 2 1 ∞ 1 = 1∞ + − w ∞ c u c u u 动能头Hd 静能头Hp 定义:单位重量流体流经叶 轮后静压能的增量Hp与理 论能头HT之比.ρ= Hp / HT HT∞ =(c2u∞ u2 – c1u∞ u1)/g

章离心泵的基本方程 第三节反作用度 反作用度p与B2的关系 B2A的极值 H.F[(c2u2-c1u2)+(c2x2-c1r2)]/2g≈c2u2/2g p=1-Ha/H≈1-(c2u2/2g)/(c2u2/g)=1-c2u/2u2 p-0时,c2uF2u2→B2 Amax-ctg(u2/C2r p=1时,c2u=0→B2 Amin=ctg(u/c2 2Amin p=1/2,C2uFu2,B2A90° 反作用度p与B2的关系 P=1-C2u/2u2=1/2+C2rctg B 2A/2u2 HT=(u2-C2rctg B 2A)u2/g Hr=Ha=2u22 /g 0 Ha=(u2 -c2rctg B2A)2/2g 名 离心泵 P24=15°≈40° 离心压缩机 B24=30°60° ctg B 2Amin P2AF90° ctg B 2Amax 高速泵 B24=90°
第 2 章 离心泵的基本方程 第三节 反作用度 反作用度ρ与β2A的关系 ρ=1- Hd / HT≈1-(c2u 2 /2g)/(c2uu2 /g)=1-c2u/2u2 β2Amax u2 c2 c2 β2Amin c2u c2r β2A的极值 Hd=[(c2u 2-c1u 2)+ (c2r 2-c1r 2)]/2g≈c2u 2/2g ρ=1-c2u/2u2=1/2+ c2rctgβ2A/2u2 HT = (u2 -c2rctgβ2A)u2/g Hd=(u2 -c2rctgβ2A)2/2g HT= Hd=2u2 2 /g ρ ρ=1 Hp ctgβ2Amin β2A=90° ctgβ2Amax ρ=0时, c2u=2u2→β2Amax=π-ctg-(u2/c2r) ρ=1时, c2u=0→β2Amin=ctg-(u2/c2r) ρ=1/2, c2u=u2, β2A=90° 反作用度ρ与β2A的关系 β2A=30°~60° 高速泵 离心泵 β2A=15°~40° 离心压缩机 β2A=90°