
基于任务优先图的任务调度 案例2:优先级定义 案例2假定只有两个处理器。优先图中不同节点的等 级不相同。下面的算法生成一个优先图: 假定有k个终止节点(无后续节点),从1到k依次标记这些 节点。 ● 令S是没有被分配(未被标记)的节点的集合,并且其中每 个节点的后续节点都已被标记,从中选一个标记成。方法如 下: 01 令exu)是u的所有直接后续节点的标记的升序排列。 若对S中所有u'(u'u),lexu<lexu)(字典序),那么u可以 赋予i
基于任务优先图的任务调度 案例2:优先级定义 ⚫ 案例2假定只有两个处理器。优先图中不同节点的等 级不相同。下面的算法生成一个优先图: ⚫ 假定有k个终止节点(无后续节点),从1到k依次标记这些 节点。 ⚫ 令S是没有被分配(未被标记)的节点的集合,并且其中每 个节点的后续节点都已被标记,从中选一个标记成i。方法如 下: ⚫ 令lex(u)是u的所有直接后续节点的标记的升序排列。 若对S中所有u’(u’≠u), lex(u)<lex(u’) (字典序),那么u可以 赋予i
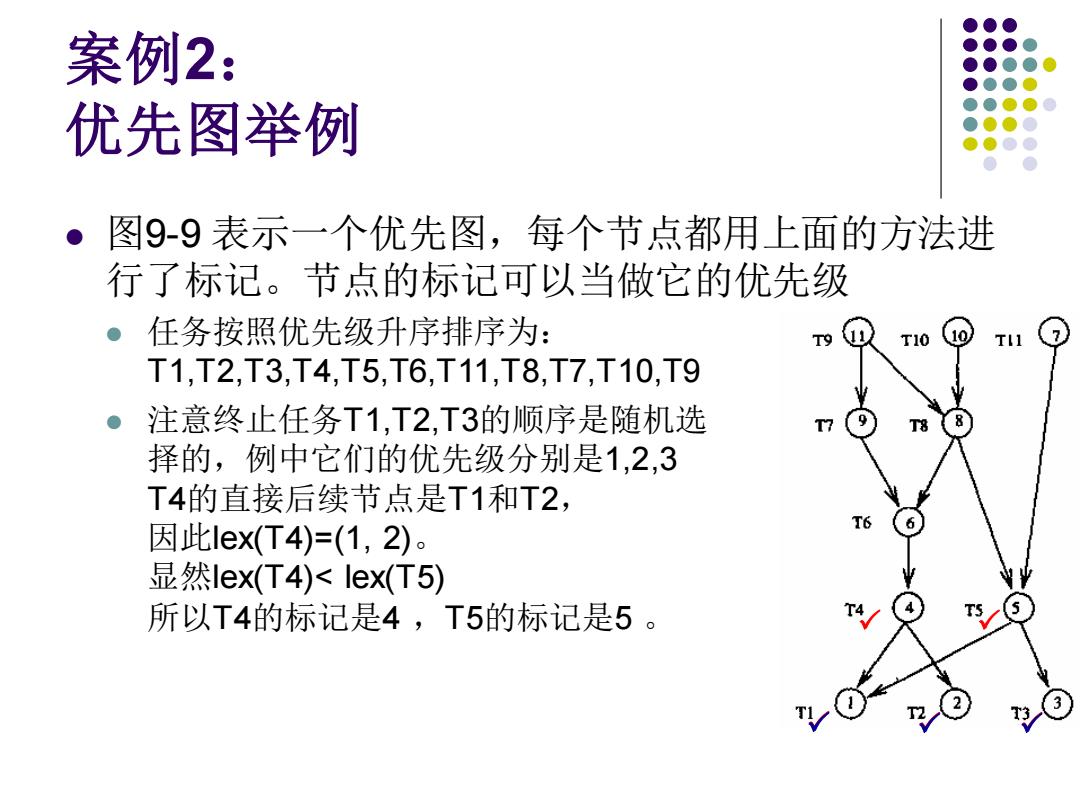
案例2: 优先图举例 。图9-9表示一个优先图,每个节点都用上面的方法进 行了标记。节点的标记可以当做它的优先级 任务按照优先级升序排序为: T10 TI T1,T2,T3,T4,T5,T6,T11,T8,T7,T10,T9 ● 注意终止任务T1,T2,T3的顺序是随机选 T 择的,例中它们的优先级分别是1,2,3 T4的直接后续节点是T1和T2, 因此lex(T4)=(1,2)。 显然Iex(T4)<lex(T5) 所以T4的标记是4,T5的标记是5
案例2: 优先图举例 ⚫ 图9-9 表示一个优先图,每个节点都用上面的方法进 行了标记。节点的标记可以当做它的优先级 ⚫ 任务按照优先级升序排序为: T1,T2,T3,T4,T5,T6,T11,T8,T7,T10,T9 ⚫ 注意终止任务T1,T2,T3的顺序是随机选 择的,例中它们的优先级分别是1,2,3 T4的直接后续节点是T1和T2, 因此lex(T4)=(1, 2)。 显然lex(T4)< Iex(T5) 所以T4的标记是4 ,T5的标记是5 。
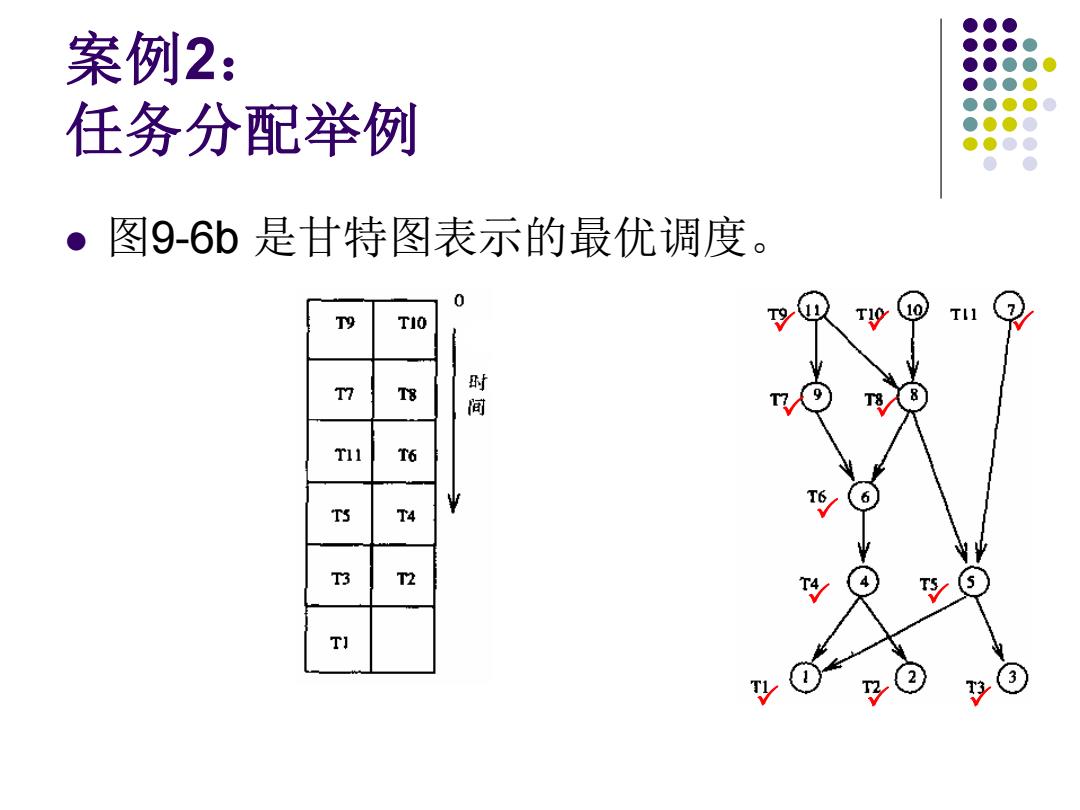
案例2: 任务分配举例 。图9-6b是甘特图表示的最优调度。 0 T10 10 T9 T10 T7 T8 间 T11 T6 T5 T4 T3 T2 TI
案例2: 任务分配举例 ⚫ 图9-6b 是甘特图表示的最优调度。

基于任务相互关系图的任务调度 任务图定义 第二个任务调度模型是利用任务相互关系图和 进程的集合来表示应用程序 ●任务相互关系图由无向图GV,E)表示 V:是进程的集合 E:是边的集合, 其中每条边表示两个通信进程间的相互作用关系,用相 关两个进程的通信代价标记(不是优先关系)
基于任务相互关系图的任务调度 任务图定义 ⚫ 第二个任务调度模型是利用任务相互关系图和 进程的集合来表示应用程序。 ⚫ 任务相互关系图由无向图Gt (Vt , Et )表示 Vt:是进程的集合 Et:是边的集合, 其中每条边表示两个通信进程间的相互作用关系,用相 关两个进程的通信代价标记(不是优先关系)

基于任务相互关系图的任务调度 处理器图定义 与任务优先图模型不同的是处理器间通信在任务相互 关系图调度模型中有重要作用。 特别地,处理器图由G(V,E)表示 顶点集V,中每个元素是一个处理器 边集E。中每个元素是一个通信信道 一般来说,VsV,因此可以假设任务划分已经完 成。然后,进行分配M:V→V,以及执行时间的估计。 注意,w(U)和w(u,V)分别表示节点u和链接(u,V)的代 价
基于任务相互关系图的任务调度 处理器图定义 ⚫ 与任务优先图模型不同的是处理器间通信在任务相互 关系图调度模型中有重要作用。 ⚫ 特别地,处理器图由Gp (Vp , Ep )表示 顶点集Vp中每个元素是一个处理器 边集Ep中每个元素是一个通信信道 ⚫ 一般来说,|Vt |≤|Vp |,因此可以假设任务划分已经完 成。然后,进行分配M:Vt→Vp以及执行时间的估计。 注意,w(u)和w(u, v)分别表示节点u和链接(u, v)的代 价