电子科技大学：《算法设计与分析 Algorithms Design and Analysis》课程教学资源（课件讲稿）第三章 动态规划 Dynamic Programming

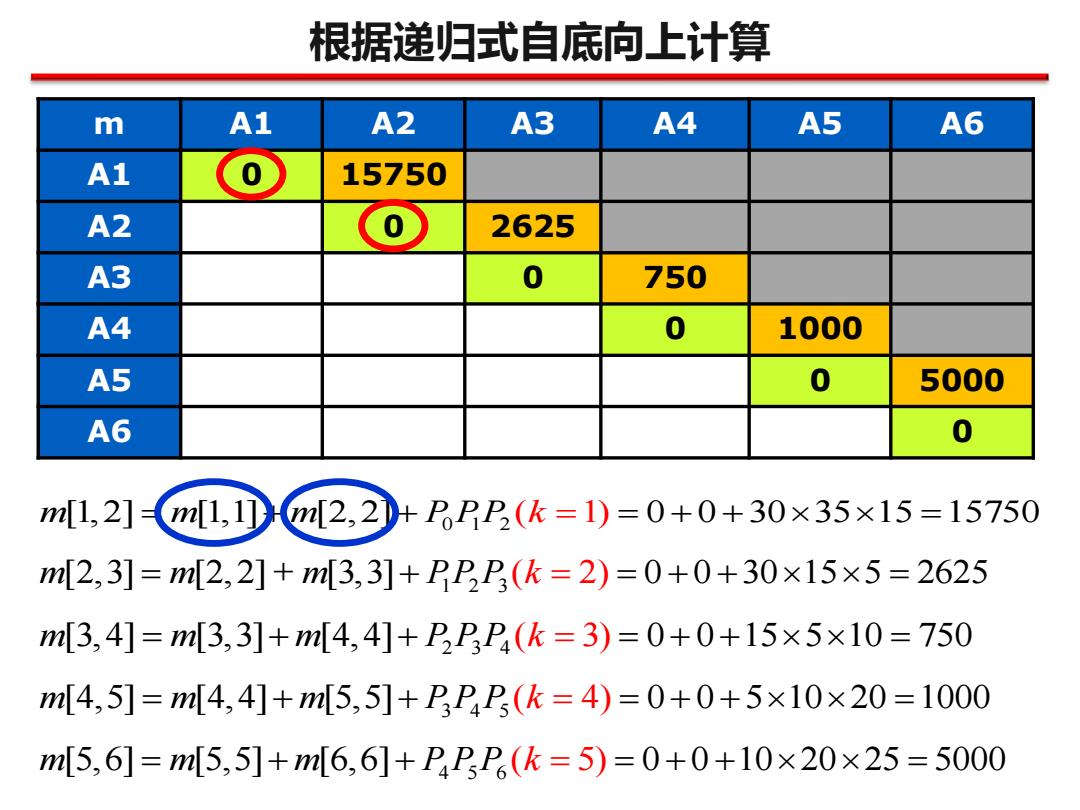
根据递归式自底向上计算 m A1 A2 A3 A4 A5 A6 A1 15750 A2 2625 A3 0 750 A4 0 1000 A5 0 5000 A6 0 m[1,2] m[1,1) m[2,2 + PPP(k=1)=0+0+30×35×15=15750 m[2,3]=ml2,2]+m3,3]+PPP(k=2)=0+0+30×15×5=2625 m3,4]=m3,3]+m4,4]+PPP(k=3)=0+0+15×5×10=750 m[4,5]=m[4,4]+m[5,5]+PP,P(k=4)=0+0+5×10×20=1000 m[5,6]=m[5,5]+m[6,6]+PPP(k=5)=0+0+10×20×25=5000

根据递归式自底向上计算 m A1 A2 A3 A4 A5 A6 A1 0 15750 A2 0 2625 A3 0 750 A4 0 1000 A5 0 5000 A6 0 0 1 2 m m m P PP [1,2] [1,1] [2,2] 0 0 30 35 15 15 5 = + + = + +   = ( 1) k = 7 0 1 2 3 m m m PP P [2,3] [2,2] + [3,3] 0 0 30 15 5 2625 = + = + +   = ( 2) k = 234 m m m P P P [3,4] [3,3] [4,4] = + + = + +   = (k = 3) 0 0 15 5 10 750 345 m m m P P P [4,5] [4,4] [5,5] = + + = + +   = (k = 4) 0 0 5 10 20 1000 4 5 6 m m m P P P [5,6] [5,5] [6,6] 0 0 10 20 25 5000 = + + = + +   = ( 5) k =

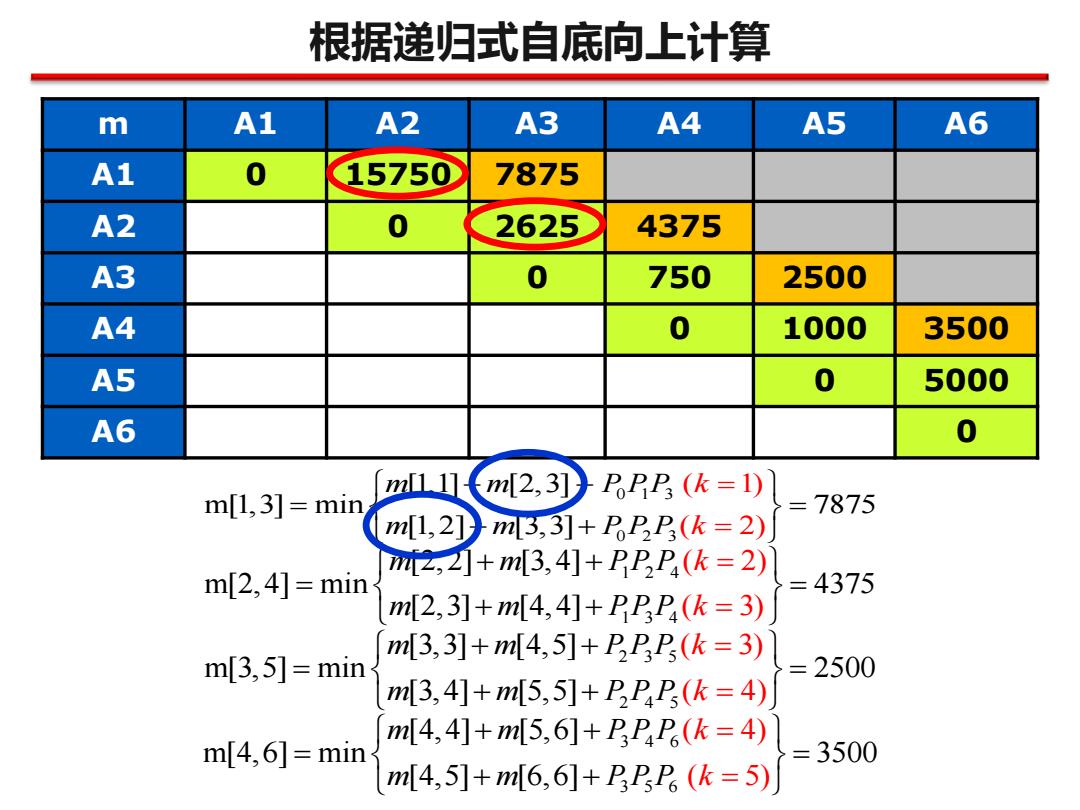
根据递归式自底向上计算 m A1 A2 A3 A4 A5 A6 A1 0 15750 7875 A2 0 2625 4375 A3 0 750 2500 A4 0 1000 3500 A5 0 5000 A6 0 m11m[2,3]) m[1,3]=min PoPP (k=1) 7875 m[1,2] m3,3)]+PP(k=2) 2,2+m[3,4]+PPP,(k=2) m[2,4]=min =4375 m[2,3]+m[4,4]+PPP(k=3) m3,3]+m[4,5]+PPP(k=3) m[3,5]=min =2500 m3,4]+m[5,5]+PPaP,(k=4) m[4,4]+m[5,6]+PPP(k=4) m[4,6]=min =3500 m[4,5]+m[6,6]+PPP(k=5)

根据递归式自底向上计算 m A1 A2 A3 A4 A5 A6 A1 0 15750 7875 A2 0 2625 4375 A3 0 750 2500 A4 0 1000 3500 A5 0 5000 A6 0 013 0 2 3 [1,1] [2,3] m[1,3] min 7875 [1,2] ( 1) [3,3] ( 2) m m P PP m k m P P P k   + + = =     = + + = 1 2 4 1 3 4 [2,2] [3,4] m[2,4] min 4375 [2,3] ( 2) [4,4] ( 3) m m PP P m k m PP P k   + + = =     = + + = 2 3 5 2 4 5 [3,3] [4,5] m[3,5] min 2500 [3,4] ( 3) [5,5] ( 4) m m P P P m k m P P P k   + + = =     = + + = 3 4 6 3 5 6 [4,4] [5,6] m[4,6] min 3500 [4,5] ( 4) [6,6] ( 5) m m P P P m k m P P P k   + + = =     = + + =

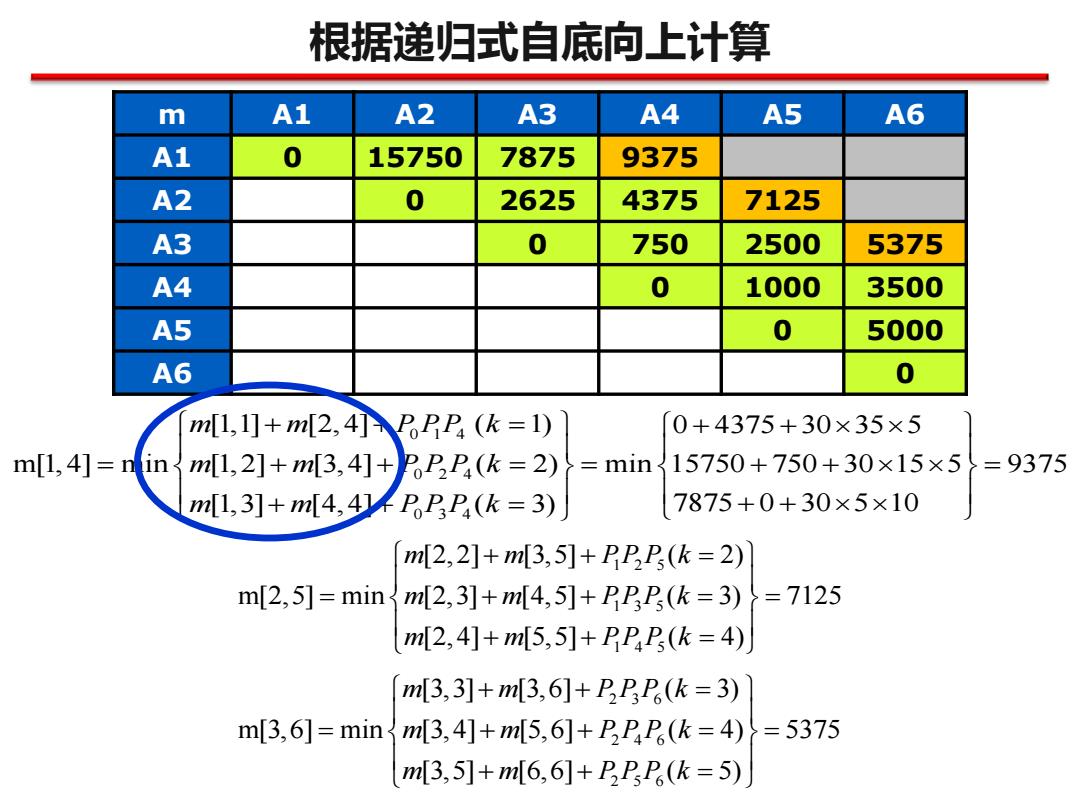
根据递归式自底向上计算 m A1 A2 A3 A4 A5 A6 A1 0 15750 7875 9375 A2 0 2625 4375 7125 A3 0 750 2500 5375 A4 0 1000 3500 A5 0 5000 A6 0 m[1,1]+m[2,4P(k=1) 0+4375+30×35×5 m[l,4]=ninm[1,2]+m[3,4]+PP(k=2) =min{15750+750+30×15×5=9375 m[1,3]+m[4,4FPPP(k=3) 7875+0+30×5×10 m2,2]+m[3,5]+22(k=2) m[2,5]=minm2,3]+m4,5]+EP,(k=3)=7125 m[2,4]+m5,5]+PPP(k=4) m[3,3]+m[3,6]+PPP(k=3) m[3,6]=min ml[3,4]+m[5,6]+卫P,P,(k=4)=5375 m[3,5]+mM[6,6]+PP,P(k=5)

根据递归式自底向上计算 m A1 A2 A3 A4 A5 A6 A1 0 15750 7875 9375 A2 0 2625 4375 7125 A3 0 750 2500 5375 A4 0 1000 3500 A5 0 5000 A6 0 0 1 4 024 034 [1,1] [2,4] ( 1) 0 4375 30 35 5 m[1,4] min [1,2] [3,4] ( 2) min 15750 750 30 15 5 9375 [1,3] [4,4] ( 3) 7875 0 30 5 10   + + =   + +       = + + = = + +   =           + + =   + +   m m P PP k m m P P P k m m P P P k 1 2 5 1 3 5 1 4 5 [2,2] [3,5] ( 2) m[2,5] min [2,3] [4,5] ( 3) 7125 [2,4] [5,5] ( 4) m m PP P k m m PP P k m m PP P k   + + =   = + + = =       + + = 2 3 6 2 4 6 2 5 6 [3,3] [3,6] ( 3) m[3,6] min [3,4] [5,6] ( 4) 5375 [3,5] [6,6] ( 5) m m P P P k m m P P P k m m P P P k   + + =   = + + = =       + + =

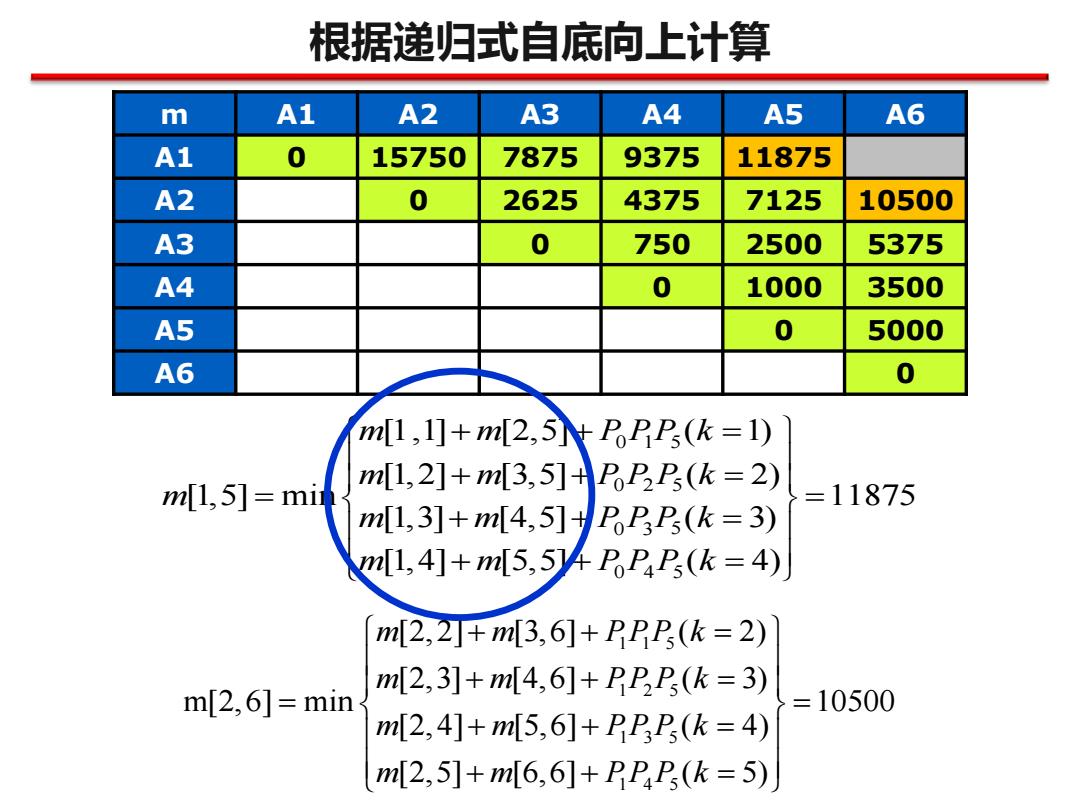
根据递归式自底向上计算 m A1 A2 A3 A4 A5 A6 A1 0 15750 7875 9375 11875 A2 0 2625 4375 7125 10500 A3 0 750 2500 5375 A4 0 1000 3500 A5 0 5000 A6 0 m[1,1]+m2,5tPPP(k=1) m1,5]=mi m[1,2]+m[3,5]+HPP2P(k=2) =11875 m[1,3]+m[4,5]+PPP(k=3) m[l,4]+m[5,54PP(k=4) m2,2+m3,6]+PPP(k=2) m2,3]+m[4,6]+PPP,(k=3) m[2,6]=min =10500 m[2,4]+m[5,6]+PPP,(k=4) m[2,5]+m[6,6]+PPP(k=5)

根据递归式自底向上计算 m A1 A2 A3 A4 A5 A6 A1 0 15750 7875 9375 11875 A2 0 2625 4375 7125 10500 A3 0 750 2500 5375 A4 0 1000 3500 A5 0 5000 A6 0 0 1 5 0 2 5 0 3 5 0 4 5 [1,1] [2,5] ( 1) [1,2] [3,5] ( 2) [1,5] min 11875 [1,3] [4,5] ( 3) [1,4] [5,5] ( 4) m m P PP k m m P P P k m m m P P P k m m P P P k               + + = + + = = = + + = + + = 1 1 5 1 2 5 1 3 5 1 4 5 [2,2] [3,6] ( 2) [2,3] [4,6] ( 3) m[2,6] min 10500 [2,4] [5,6] ( 4) [2,5] [6,6] ( 5) m m PPP k m m PP P k m m PP P k m m PP P k   + + =     + + = = =   + + =       + + =

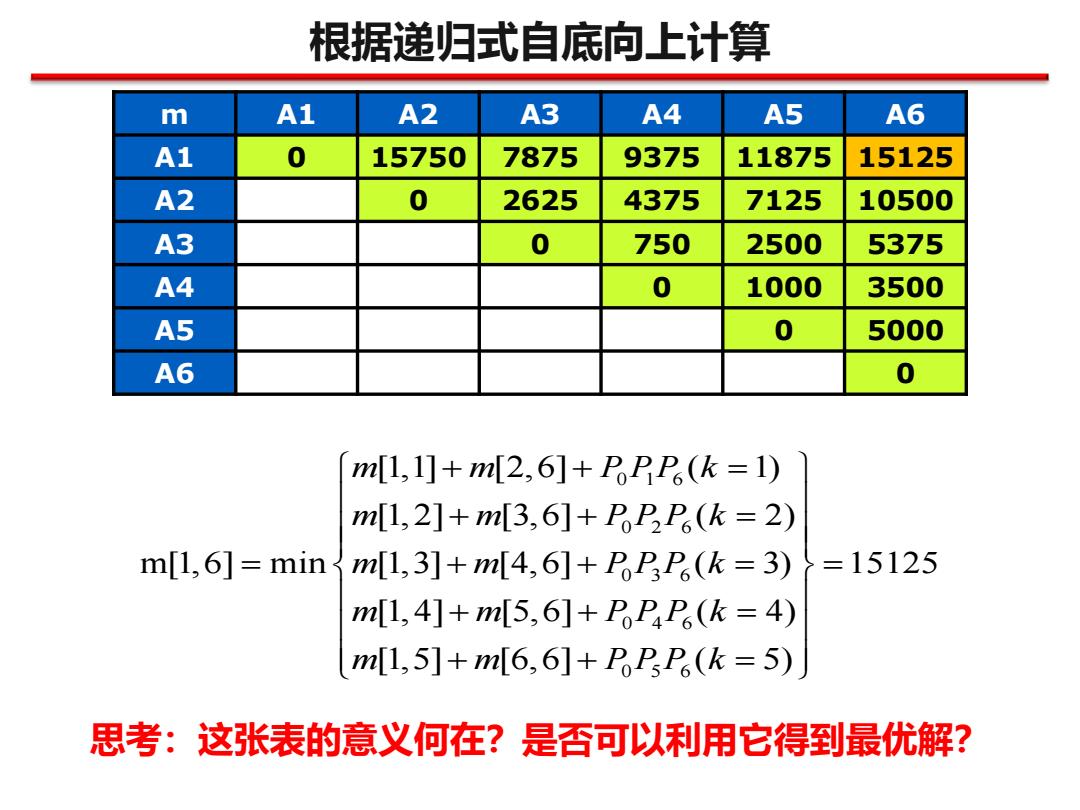
根据递归式自底向上计算 m A1 A2 A3 A4 A5 A6 A1 0 15750 7875 9375 11875 15125 A2 0 2625 4375 7125 10500 A3 0 750 2500 5375 A4 0 1000 3500 A5 0 5000 A6 0 m1,1]+m[2,6]+PPP(k=1) m[1,2]+m[3,6]+PPP。(k=2) m[1,6]=minm[1,3]+m[4,6]+PPP(k=3) =15125 m[1,4]+m[5,6]+PP4P。(k=4) m[1,5]+m[6,6]+PPP(k=5) 思考：这张表的意义何在？是否可以利用它得到最优解？

根据递归式自底向上计算 m A1 A2 A3 A4 A5 A6 A1 0 15750 7875 9375 11875 15125 A2 0 2625 4375 7125 10500 A3 0 750 2500 5375 A4 0 1000 3500 A5 0 5000 A6 0 0 1 6 0 2 6 0 3 6 0 4 6 0 5 6 [1,1] [2,6] ( 1) [1, 2] [3,6] ( 2) m[1,6] min [1,3] [4,6] ( 3) 15125 [1, 4] [5,6] ( 4) [1,5] [6,6] ( 5) m m P PP k m m P P P k m m P P P k m m P P P k m m P P P k   + + =   + + =   = + + = =     + + =       + + = 思考：这张表的意义何在？是否可以利用它得到最优解？