
动态规划法求解矩阵连乘问题 3第四步:构造最优解对应的问题解值 需设置另一张表S:在填充表m的过程中 记录各个子矩阵链取最优值时的分割位置k ,S[i][]=k表示:A[i:j]的最优划分方式是(A[i:k])(A[k+1:j]) 可以据此构造矩阵链的最优计算次序 。从s[1,n]记录的信息可以知道A[1:n]的最佳划分方式 即:(A[1:k])(A[k+1:n])其中:k=S[1,n] 其中:A[1:k]和A[k+1:n]的最佳划分方式可以递归地得到 ,即:(A[1:x])(A[x+1:k]) 其中:X=S[1,k] 和:(A[k+1:y])(A[y+1:n])其中:y=S[k+1,n] 由此递归下去,可以得到最优完全加括号方式,即构造出一个最优解
动态规划法求解矩阵连乘问题 第四步:构造最优解对应的问题解值 需设置另一张表 S :在填充表 m 的过程中 ⚫ 记录各个子矩阵链取最优值时的分割位置k ⚫ S[i][j]=k表示:A[i:j] 的最优划分方式是 (A[i:k])(A[k+1:j]) 可以据此构造矩阵链的最优计算次序 ⚫ 从s[1,n]记录的信息可以知道A[1:n]的最佳划分方式 ⚫ 即:(A[1 : k])(A[k+1 : n]) 其中:k = S[1, n] ⚫ 其中:A[1 : k]和A[k+1:n]的最佳划分方式可以递归地得到 ⚫ 即:(A[1 : x])(A[x+1: k]) 其中:x = S[1, k] ⚫ 和:(A[k+1 : y])(A[y+1: n]) 其中:y = S[k+1, n] 由此递归下去,可以得到最优完全加括号方式,即构造出一个最优解
最优解? 构造最优解 最优值? m A1 A2 A3 A4 A5 A6 A1 0 15750 7875 9375 11875 15125 A2 0 2625 4375 7125 10500 A3 0 750 2500 5375 A4 0 1000 3500 A5 0 5000 A6 0 S 1 2 3 4 5 6 1 0 1 1 3 3 3 2 0 2 3 3 3 3 0 3 3 3 4 0 4 5 5 0 5 6 0 该矩阵连乘问题的最优解为:(A1(A2A3))((A4A5)A6)
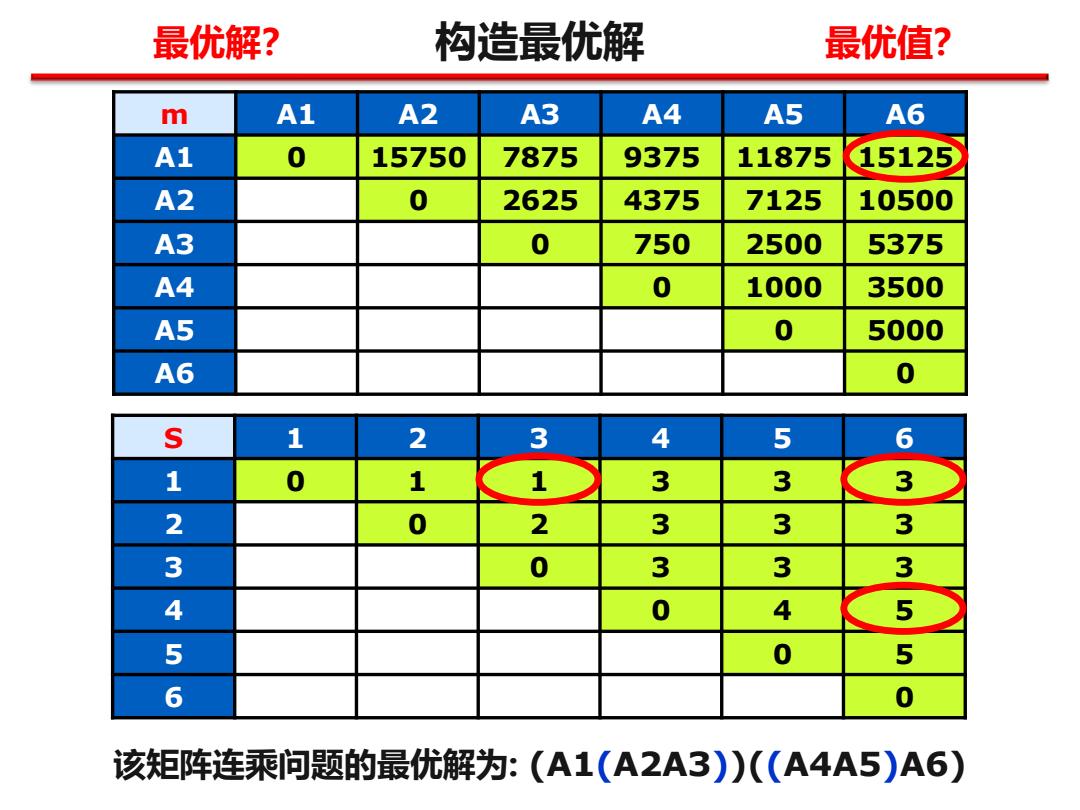
构造最优解 m A1 A2 A3 A4 A5 A6 A1 0 15750 7875 9375 11875 15125 A2 0 2625 4375 7125 10500 A3 0 750 2500 5375 A4 0 1000 3500 A5 0 5000 A6 0 S 1 2 3 4 5 6 1 0 1 1 3 3 3 2 0 2 3 3 3 3 0 3 3 3 4 0 4 5 5 0 5 6 0 该矩阵连乘问题的最优解为: (A1(A2A3))((A4A5)A6) 最优解? 最优值?

构造最优解 上述算法中,s[1.n,1.n]记录了各个子矩阵链取最优值时 分割位置k。 Φs[i,j]表示A[i,j]的最佳方式是(A[i,k])(A[k+1,j])。 从s[1,n]记录的信息可以知道A[1,n]的最佳方式,它是 (A[1,s[1,n]])(A[s[1,n]+1,n])。 其中,A[1,s[1,n]最佳方式可以递归地得到,它是 (A[1,s[1,s[1,n]])(A[s[1,s[1,n]+1,s[1,s[1,n]]) 由此递归下去,可以得到最优完全加括号方式,即构造出一个 最优解
构造最优解 上述算法中,s[1..n,1..n]记录了各个子矩阵链取最优值时 分割位置k。 s[i,j]表示A[i,j]的最佳方式是(A[i,k])(A[k+1,j])。 从s[1,n]记录的信息可以知道A[1,n]的最佳方式,它是 (A[1,s[1,n]])(A[s[1,n]+1,n])。 其中,A[1,s[1,n]]最佳方式可以递归地得到,它是 (A[1,s[1,s[1,n]]])(A[s[1,s[1,n]]+1,s[1,s[1,n]]]) 由此递归下去,可以得到最优完全加括号方式,即构造出一个 最优解

构造最优解 ●构造最优解的过程是一个递劃归过程 ●算法: Pubic void TraceBack(ints,int i,int j) { if(i==j)return; TraceBack(s,i,s[i,j]); TraceBack(s,s[i,j]+1,j); System.out.println(“Multiply A”+i+,”+s[i,j]+ ”andA”+(s[i,j]+i)+,”+j); ●算法的调用: void mainO)f int0P={3035,155,10,20,25}; int n=P.length; int[n][n]m,s; MatrixChain(P,n,m,s);/动态规划算法 TraceBack(s,1,n); }
构造最优解 ⚫构造最优解的过程是一个递归过程 ⚫算法: ⚫算法的调用: Pubic void TraceBack( int[ ][ ] s,int i,int j) { if(i==j) return; TraceBack(s,i,s[i,j]); TraceBack(s,s[i,j]+1,j); System.out.println(“Multiply A”+i+” , ”+s[i,j]+ ”and A”+(s[i,j]+1)+”,”+j); } void main(){ int[] P={30,35,15,5,10,20,25}; int n=P.length; int[n][n] m,s; MatrixChain(P,n,m,s); //动态规划算法 TraceBack(s,1,n); }

动态规划方法 MatrixChain(形参表) 3{ 初始化是将m,即对 c3初始化; 角线元素,赋值为0。 自底向上地计算每一个m[[j]并将结果填入表 中。 3} 底是m,即对角线元 素。最顶层是m[1川n
MatrixChain(形参表) { 初始化; 自底向上地计算每一个m[i][j]并将结果填入表 中。 } 底是m[i][i],即对角线元 素。最顶层是m[1][n]。 初始化是将m[i][i],即对 角线元素,赋值为0。 动态规划方法