
矩阵连乘问题 3第一步:分析最优解的结构 上述划分的关键特征在于: 中A[1:n]的一个最优计算次序所包含的矩阵子链也是最优的 Φ即:A[1:k]和A[k+1:n]的计算次序也是最优的 3 最优子结构性质 矩阵连乘计算次序问题的最优解包含着其子问题的最优解 这种性质称为最优子结构性质 Φ该性质是该问题是否可用动态规划算法求解的显著特征之一!
矩阵连乘问题 第一步:分析最优解的结构 上述划分的关键特征在于: A[1:n]的一个最优计算次序所包含的矩阵子链也是最优的 即:A[1:k]和A[k+1:n]的计算次序也是最优的 最优子结构性质 矩阵连乘计算次序问题的最优解包含着其子问题的最优解 这种性质称为最优子结构性质 该性质是该问题是否可用动态规划算法求解的显著特征之一!

动态规划法求解矩阵连乘问题 3第二步:建立递归系(递归地定义最优值) 中设:计算A[ij]所需要的最少数乘次数为m[i][j] (1≤isjsn) 则:原问题的最优值为m[1][n] 当i=j时,A[ij]=A,因此:m[i门[i]=0 Φ当i<j时,可利用最优子结构性质来计算m[]: ·设:A的维度为P-1xP,假设A[ij]的最优划分位置为k 。 则:m[=m[[k+m[k+1]]+P1PkP) k的取值只有-i个可能,即:k∈{i,i+1,,j1} k是其中使计算量达到最小的位置,因此[][们可定义为 i- i=j min {mli,k]+mlk+1,j]+pppi i< j<k<j
动态规划法求解矩阵连乘问题 第二步:建立递归关系(递归地定义最优值) 设:计算A[i:j]所需要的最少数乘次数为m[i][j] (1≤i≤j≤n) 则:原问题的最优值为m[1][n] 当 i=j 时,A[i:j]=Ai,因此:m[i][i]=0 当 i<j 时,可利用最优子结构性质来计算m[i][j]: • 设:Ai 的维度为 Pi-1 x Pi ,假设A[i:j]的最优划分位置为k • 则:m[i][j]=m[i][k]+m[k+1][j]+ Pi-1 Pk Pj • k的取值只有j-i个可能,即:k∈{i, i+1, ..., j-1} • k是其中使计算量达到最小的位置,因此m[i][j]可定义为 + + + = = − m i k m k j p p p i j i j m i j i k j min{ [ , ] [ 1, ] } 0 [ , ] 1 i k j

动态规划法求解矩阵连乘问题 第三步:计算最优值 简单地递归计算m[1][n]将耗费指数时间 在递劃归计算时,许多子问题被重复计算多次 考虑1≤i≤j≤n的所有可能情况 不同的有序对(,)对应于不同的子问题 因此,不同子问题的个数最多只有: n(n-1)_n2-n 2 2 2 Φ 这也是该问题可用动态规划算法求解的又一显著特征 采用动态规划法,可依据其递归式以自底向上的方式进行计算 在计算过程中,保存已解决的子问题答案 每个子问题只计算一次,而在后面需要时只要简单查一下, 从而避免大量的重复计算,最终得到多项式时间的算法
动态规划法求解矩阵连乘问题 第三步:计算最优值 简单地递归计算m[1][n]将耗费指数时间 • 在递归计算时,许多子问题被重复计算多次 考虑 1≤i≤j≤n 的所有可能情况 • 不同的有序对 (i, j) 对应于不同的子问题 • 因此,不同子问题的个数最多只有: 2 ( 1) 2 2 2 n n n n n − − = = 这也是该问题可用动态规划算法求解的又一显著特征 采用动态规划法,可依据其递归式以自底向上的方式进行计算 • 在计算过程中,保存已解决的子问题答案 • 每个子问题只计算一次,而在后面需要时只要简单查一下, 从而避免大量的重复计算,最终得到多项式时间的算法
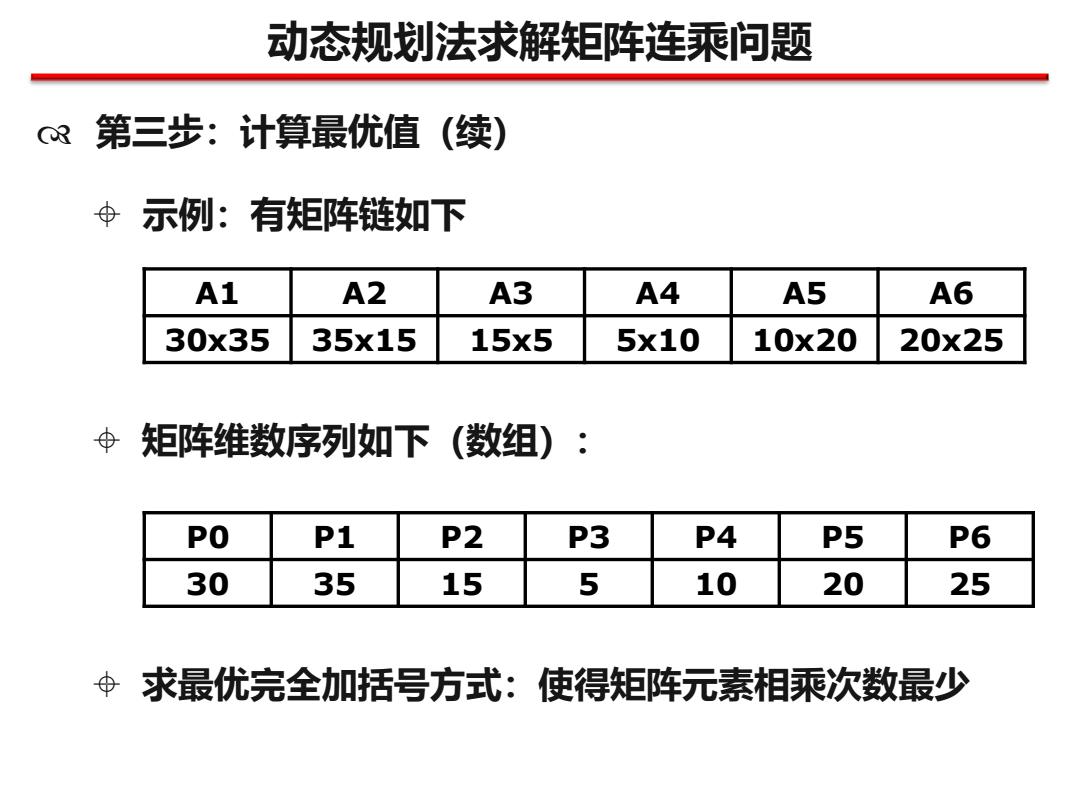
动态规划法求解矩阵连乘问题 3第三步:计算最优值(续) Φ示例:有矩阵链如下 A1 A2 A3 A4 A5 A6 30x35 35x15 15x5 5x10 10x20 20x25 Φ矩阵维数序列如下(数组) PO P1 P2 P3 P4 P5 P6 30 35 15 5 10 20 25 Φ求最优完全加括号方式:使得矩阵元素相乘次数最少
动态规划法求解矩阵连乘问题 第三步:计算最优值(续) 示例:有矩阵链如下 矩阵维数序列如下(数组): A1 A2 A3 A4 A5 A6 30x35 35x15 15x5 5x10 10x20 20x25 P0 P1 P2 P3 P4 P5 P6 30 35 15 5 10 20 25 求最优完全加括号方式:使得矩阵元素相乘次数最少
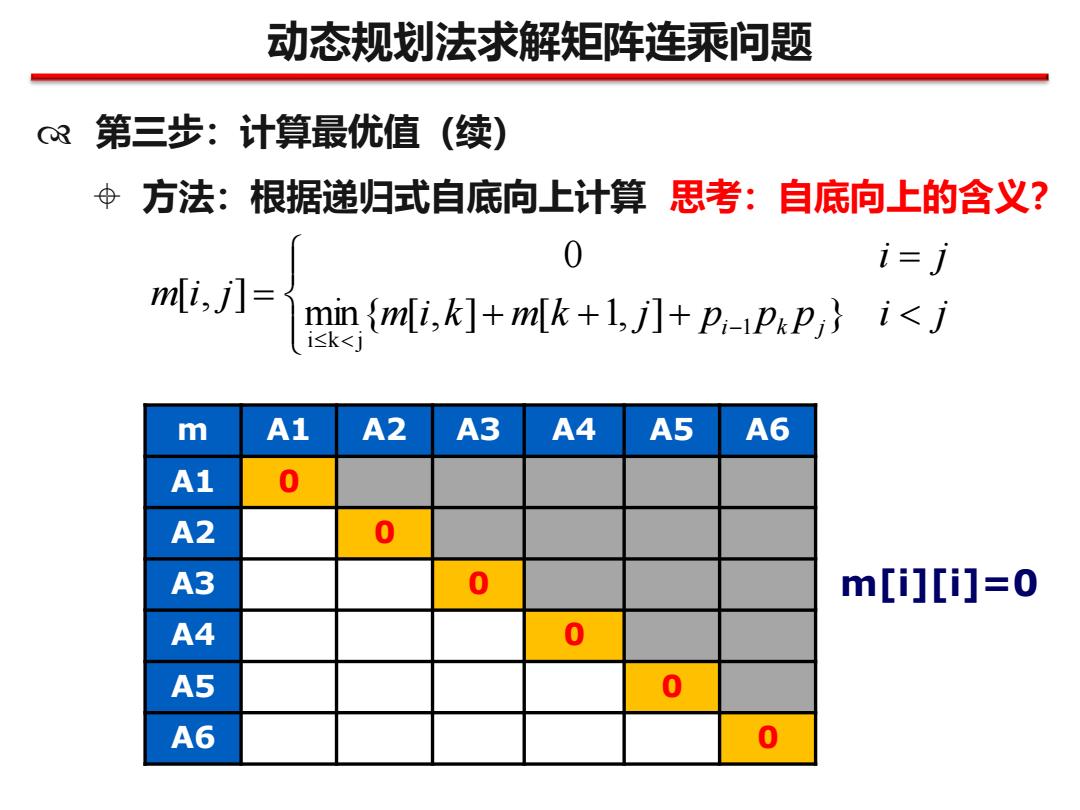
动态规划法求解矩阵连乘问题 R 第三步:计算最优值(续) Φ方法:根据递归式自底向上计算 思考:自底向上的含义? 0 i=j m[i,j]=了 min {mli,k]+mlk+1,j]+pppi}i<j i≤k<j m A1 A2 A3 A4 A5 A6 A1 A2 0 A3 0 m[i][i]=0 A4 0 A5 0 A6 0
动态规划法求解矩阵连乘问题 第三步:计算最优值(续) 方法:根据递归式自底向上计算 + + + = = − m i k m k j p p p i j i j m i j i k j min{ [ , ] [ 1, ] } 0 [ , ] 1 i k j m A1 A2 A3 A4 A5 A6 A1 0 A2 0 A3 0 A4 0 A5 0 A6 0 m[i][i]=0 思考:自底向上的含义?