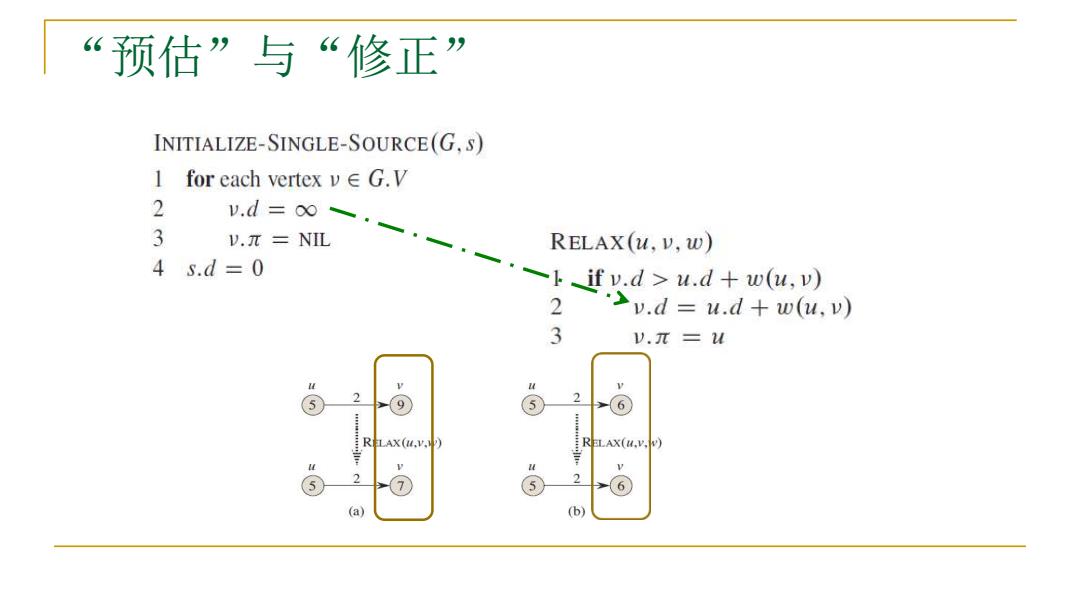
预估”与“修正” INITIALIZE-SINGLE-SOURCE(G,S) 1 for each vertex v G.V 2 3 v.d=·. ).π=NIL RELAX(u,v,w) 4s.d=0 -ifv.d>u.d+w(u,v) 2 '>v.d u.d+w(u.v) 3 V.π=2u 2 ⑤ (6 RLAX(u.V) RELAX(u.v.Wv) ⑦ ⑤ 2 (a) (b)
“预估”与“修正
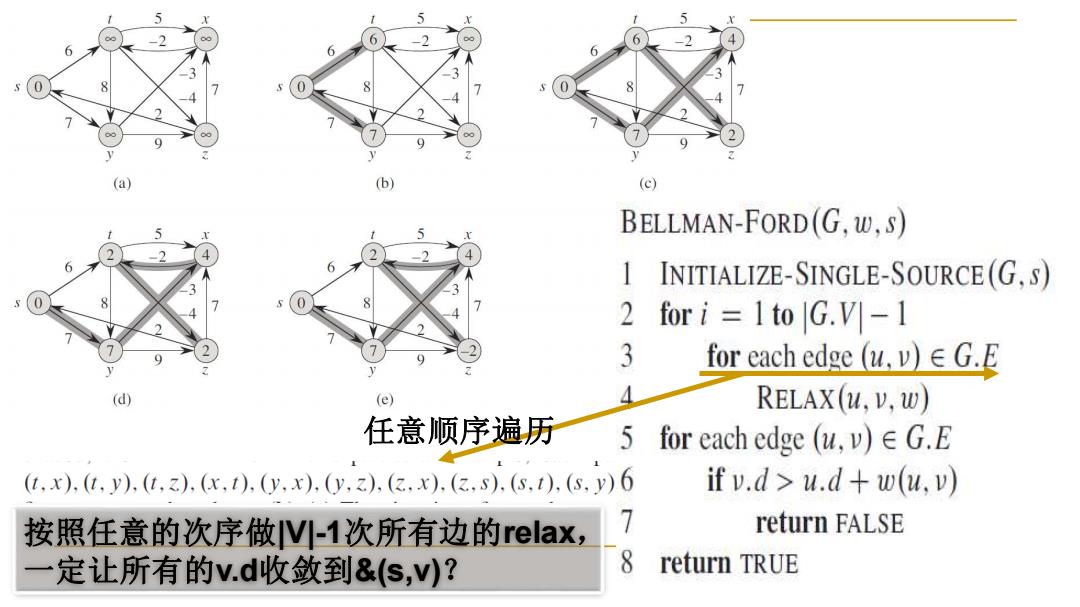
6 (a) (c) BELLMAN-FORD(G,w,s) 6 1 INITIALIZE-SINGLE-SOURCE(G.S) 2 for i 1to |G.V]-1 3 for each edge (u.v)G.E (d) (e) RELAX(u,v,w) 任意顺序遍历 5 for each edge (u,v)G.E (t,x),(1,y),(1,z,(x,1),y,x,y,z),(3,x),(3,s,(,),(s,y)6 if v.d>u.d+w(u,v) 按照任意的次序做V-1次所有边的relax, 7 return FALSE 定让所有的v.d收敛到&(s,v)? 8 return TRUE
任意顺序遍历 按照任意的次序做|V|-1次所有边的relax, 一定让所有的v.d收敛到&(s,v)?

我们需要对v.d进行详细观察! Lemma 24.11 (Upper-bound property) Let G =(V,E)be a weighted,directed graph with weight function w E->R. Let s e V be the source vertex,and let the graph be initialized by INITIALIZE- SINGLE-SOURCE(G,s).Then,v.d >8(s,v)for all vV,and this invariant is maintained over any sequence of relaxation steps on the edges of G.Moreover, once v.d achieves its lower bound 8(s,v),it never changes. 计算中不断变化(其实是不断“变小”) 的v.d始终是最短距离的上界!
我们需要对v.d进行详细观察! 计算中不断变化(其实是不断“变小”) 的v.d始终是最短距离的上界!

Proof We prove the invariant v.d >8(s,v)for all vertices vV by induction over the number of relaxation steps. For the basis,v.d>8(s,v)is certainly true after initialization,since v.d=oo implies v.d (s,v)for all v V-fs),and since s.d =0 >8(s,s)(note that 8(s,s)=-oo if s is on a negative-weight cycle and 0 otherwise). For the inductive step,consider the relaxation of an edge (u,v).By the inductive hypothesis,x.d =8(s,x)for all x V prior to the relaxation.The only d value that may change is v.d.If it changes,we have v.d =u.d+w(u,v) //Relax操作 之 8(,u)+w(u,v) (by the inductive hypothesis) 之 8(s,v) (by the triangle inequality), and so the invariant is maintained. To see that the value of v.d never changes once v.d =8(s,v),note that having achieved its lower bound,v.d cannot decrease because we have just shown that v.d >8(s,v),and it cannot increase because relaxation steps do not increase d values. 既不会再减小,也不会增大
既不会再减小,也不会增大 //Relax操作

问题6: “修正”最终“可能”导致2d=S,y)。 但“一定”吗?