例:设待安排的11个活动按结束时间的非减序排列如下: 1 2 3 4 5 6 7 8 9 10 11 S[i] 1 3 0 5 3 5 6 8 8 2 12 F[i] 4 5 6 7 8 9 10 11 12 13 14 0123 456789 1011121314 1 2 3 4 5 6 7 8 9 10 11 再问:这种解法能否确保全局最优?
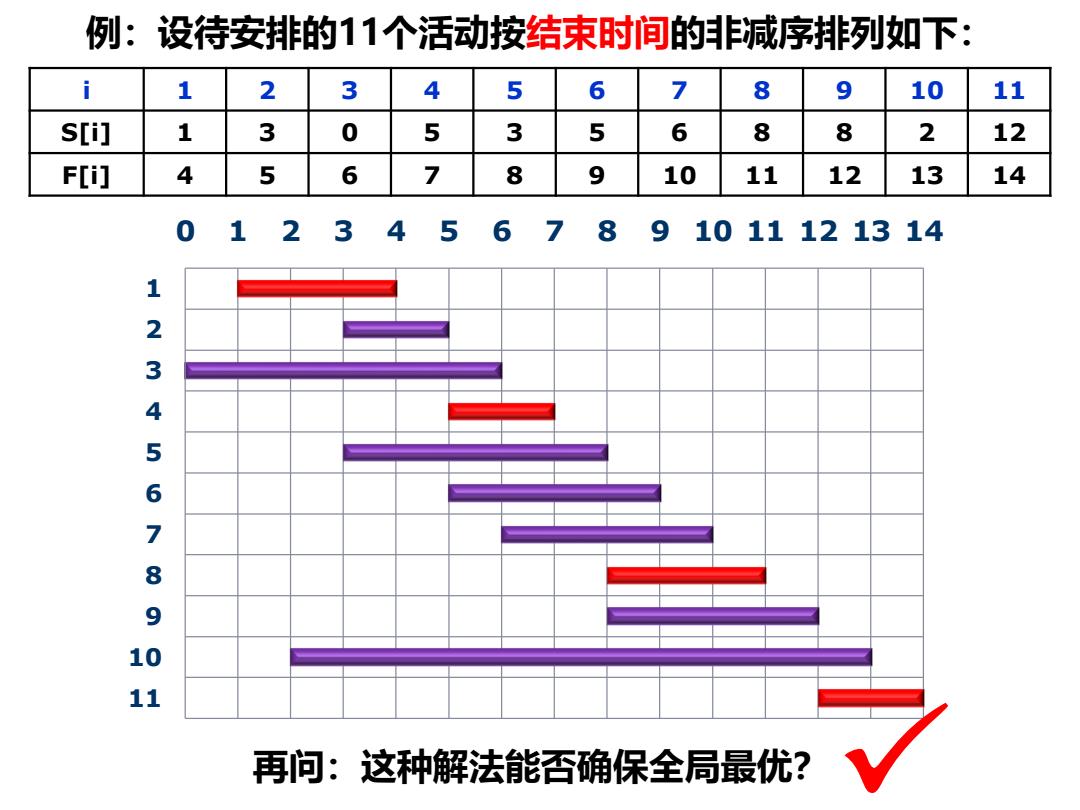
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1 2 3 4 5 6 7 8 9 10 11 例:设待安排的11个活动按结束时间的非减序排列如下: i 1 2 3 4 5 6 7 8 9 10 11 S[i] 1 3 0 5 3 5 6 8 8 2 12 F[i] 4 5 6 7 8 9 10 11 12 13 14 再问:这种解法能否确保全局最优?

证明:按F[1:n]递增顺序进行贪心选择可得全局最优解 @R 证明思路 Φ证明活动安排问题有一个最优解以贪心选择开始 Φ用数学到归纳法证明贪心算法的解是全局最优解 @3 首先证明活动安排问题有一个最优解以贪心选择开始 设:E={1,.,n}为给定活动集合(按F[k]非减序编号) 显然活动1具有最早的完成时间 设:集合A是该问题的一个最优解(元素按F[k]非减序排列) 不妨设A中的第一个活动是活动水k Φ 若k=1,则:A就是一个以贪心选择开始的最优解 若k>1,则设:B=(A-{k})U{1} 由于F[1]≤F[k],且A中活动相容,故B中活动也相容 由于B和A中包含的活动个数相同,故B也是最优的 ·得证:总存在一个以贪心选择开始的最优活动安排方案
证明:按F[1:n]递增顺序进行贪心选择可得全局最优解 证明思路 证明活动安排问题有一个最优解以贪心选择开始 用数学归纳法证明贪心算法的解是全局最优解 首先证明活动安排问题有一个最优解以贪心选择开始 设:E={1,…,n}为给定活动集合(按F[k]非减序编号) • 显然活动1具有最早的完成时间 设:集合A是该问题的一个最优解(元素按F[k]非减序排列) • 不妨设A中的第一个活动是活动k 若k=1,则:A就是一个以贪心选择开始的最优解 若k>1,则设:B=(A-{k})∪{1} • 由于F[1]≤F[k],且A中活动相容,故B中活动也相容 • 由于B和A中包含的活动个数相同,故B也是最优的 得证:总存在一个以贪心选择开始的最优活动安排方案

活动安排问题的最优子结构性质 c3设E={1,2,,}为所给的活动集合,在做了贪心选择,即选 择了活动1后,原问题就简化为对E中所有与活动1相容的活 动进行活动安排的子问题。 ?即,若A是原问题的最优解,则A'=A-{1)是活动安排问题 E'={i∈E:S;之f}的最优解。 3证明:如果能找到E'的一个解B',它包含比A'更多的 活动,则将活动1加入到B'中将产生E的一个解,它包含 比A更多的活动。这与A的最优性矛盾! 3因此:在做出贪心选择 (活动1)之后,原问题N简化为: 子问题N':对E中所有与活动1相容的活动进行安排 每一步所做的贪心选择都将问题简化为一个更小的与原 问题具有相同形式的子问题
活动安排问题的最优子结构性质 设E={1,2,…,n}为所给的活动集合,在做了贪心选择,即选 择了活动1后,原问题就简化为对E中所有与活动1相容的活 动进行活动安排的子问题。 即,若A是原问题的最优解,则A’=A-{1}是活动安排问题 E’={i∈E : si ≥ f1 }的最优解。 证明:如果能找到E’的一个解B’,它包含比A’更多的 活动,则将活动1加入到B’中将产生E的一个解,它包含 比A更多的活动。这与A的最优性矛盾! 因此:在做出贪心选择(活动1)之后,原问题N简化为: 子问题N’:对E中所有与活动1相容的活动进行安排 每一步所做的贪心选择都将问题简化为一个更小的与原 问题具有相同形式的子问题

活动安排问题 R 算法设计 Φ用数组A[1:n]来存储所选择的活动 (设活动总数为n) ·约定:若活动i在集合A中,则A[i门=1;否则A[i门=0 ⊕ 各活动的起始时间和结束时间存储于数组S[1:n]和F[1:n]中 且:数组F[1:n]已按结束时间的非减序排列(递增) 依次从F[1:n]中选择活动i,尝试加入集合A 设:变量k记录A中最近一次加入的活动:由于F[1:n]有序,所以 F[k]总是当前集合A中所有活动的最大结束时间 然后依次检查活动ⅱ是否与当前已选择的所有活动相容 若相容则将活动加入集合A中;若不相容,则放弃活动i 继续检查F[1:n]中下一个活动与集合A中活动的相容性 直到所有活动均已检查完毕,程序结束
活动安排问题 算法设计 用数组A[1:n]来存储所选择的活动(设活动总数为n) • 约定:若活动i在集合A中,则A[i]=1;否则A[i]=0 各活动的起始时间和结束时间存储于数组S[1:n]和F[1:n]中 • 且:数组F[1:n]已按结束时间的非减序排列(递增) 依次从F[1:n]中选择活动 i ,尝试加入集合A • 设:变量k记录A中最近一次加入的活动:由于F[1:n]有序,所以 F[k]总是当前集合A中所有活动的最大结束时间 • 然后依次检查活动 i 是否与当前已选择的所有活动相容 – 若相容则将活动i加入集合A中;若不相容,则放弃活动i – 继续检查F[1:n]中下一个活动与集合A中活动的相容性 – 直到所有活动均已检查完毕,程序结束

活动安排问题 3 算法设计(续) Φ新增的活动ⅰ和当前集合A中所有活动相容的充分必要条件是 ● S[门]≥F[k]:即活动ⅰ的开始时间不早于k的结束时间 k为最近加入集合A的活动 一若条件满足,则活动ⅰ取代k成为最近加入A的活动 若S[门]<F[k],则放弃活动i,转而考虑下一个活动 算法的直觉:这种选择方式为后序活动预留尽可能多的时间 由于输入的活动按照其完成时间的非减序排列 所以每次总是选择具有最早完成时间的相容活动加入集合A 贪心选择的意义在于:使剩余的可安排时间段极大化,以便 安排尽可能多的相容活动
活动安排问题 算法设计(续) 新增的活动 i 和当前集合A中所有活动相容的充分必要条件是 ⚫ S[i]≥F[k]:即活动 i 的开始时间不早于k的结束时间 ━ k为最近加入集合A的活动 ━ 若条件满足,则活动 i 取代 k 成为最近加入A的活动 ⚫ 若S[i]<F[k],则放弃活动 i ,转而考虑下一个活动 算法的直觉:这种选择方式为后序活动预留尽可能多的时间 ⚫ 由于输入的活动按照其完成时间的非减序排列 ⚫ 所以每次总是选择具有最早完成时间的相容活动加入集合A ⚫ 贪心选择的意义在于:使剩余的可安排时间段极大化,以便 安排尽可能多的相容活动