贪心算法求解活动安活动的起始时间和结束时间 存储于数组s[]和f[]中且按结 算法描述 束时间的非减序排列 Public static int greedySelector(int[s,int[f,boolean a[ int n=s.length-1; 算法用数组a[]存储所选择的活动,活 a[1]=true; 动i在集合A中,当且仅当a[i]=true int j=1; int count=l; 变量记录最近一次加入A的活动,由于 for(int=2;i长=n;t)输入的活动以其完成时间的非减序排列, 时间复杂度 if(s[i]>=fljl 财然后浓次检查靠嘉是容车普劫的最大 a[i]=true;. O(n) 前包选择的所有活动相容动1,并将 j=i; J阿U/为L count++; 若相杏列总亮当前集合撕有活动的 } 动最失结束时间如敌活和当前集合A else a[i]=false; 选鲜话动稻蓉统必要条件是其 始不阜最近症湘巢给A的活 return count; 动j的结束时间f),即s≥f行,若活动i 3 与之相容,则成为最近加入集合A中 的活动,并取代活动的位置
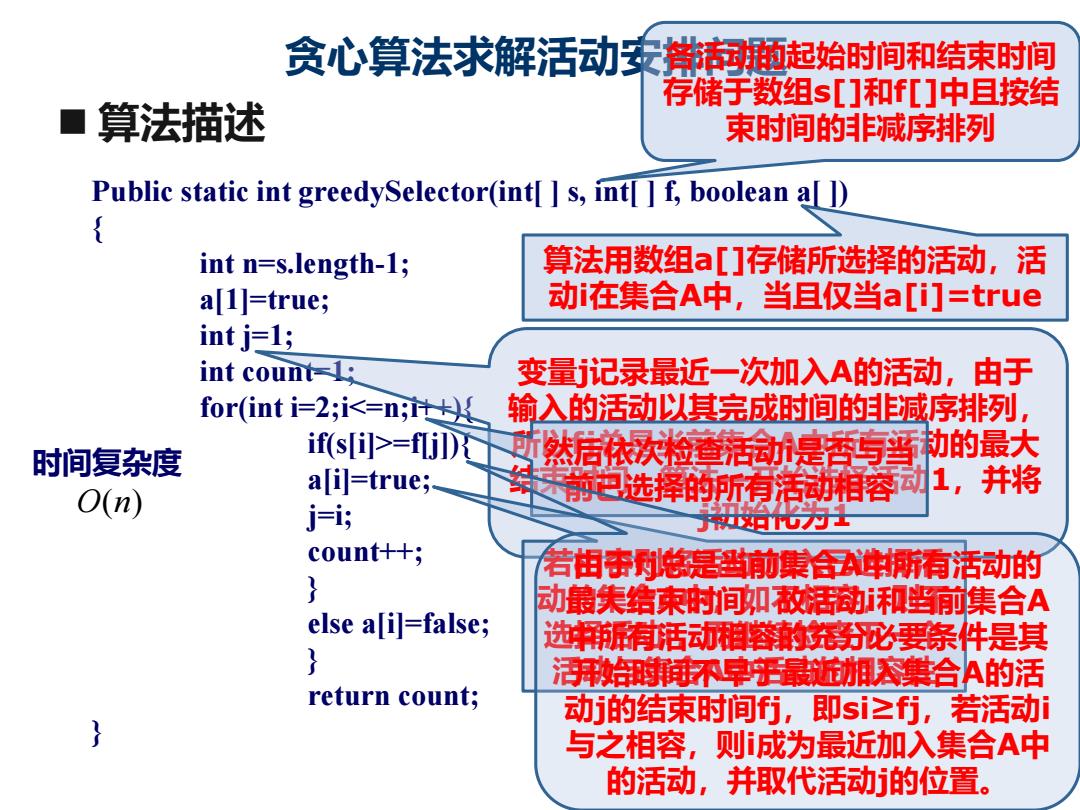
◼ 算法描述 贪心算法求解活动安排问题 Public static int greedySelector(int[ ] s, int[ ] f, boolean a[ ]) { int n=s.length-1; a[1]=true; int j=1; int count=1; for(int i=2;i<=n;i++){ if(s[i]>=f[j]){ a[i]=true; j=i; count++; } else a[i]=false; } return count; } 各活动的起始时间和结束时间 存储于数组s[]和f[]中且按结 束时间的非减序排列 算法用数组a[]存储所选择的活动,活 动i在集合A中,当且仅当a[i]=true 变量j记录最近一次加入A的活动,由于 输入的活动以其完成时间的非减序排列, 所以fj总是当前集合A中所有活动的最大 结束时间,算法一开始选择活动1,并将 j初始化为1 然后依次检查活动i是否与当 前已选择的所有活动相容 若相容则将活动i加入已选择活 动的集合A中;如不相容,则不 选择活动i,而继续检查下一个 活动与集合A中活动的相容性 由于fj总是当前集合A中所有活动的 最大结束时间,故活动i和当前集合A 中所有活动相容的充分必要条件是其 开始时间不早于最近加入集合A的活 动j的结束时间fj,即si≥fj,若活动i 与之相容,则i成为最近加入集合A中 的活动,并取代活动j的位置。 时间复杂度 O n( )

活动安排问题 R 算法分析 Φ复杂度分析:为使最多的活动能相容地使用公共资源 若活动已按结束时间的非减序排列:算法只需O()的时间 若活动未按非减序排列:可以用O(nlogn)的时间先排序 全局最优解 贪心算法并不总能求得问题的整体最优解 但对于活动安排问题,贪心算法却总能求得的整体最优解 即:它最终所确定的相容活动集合A的规模最大 这个结论可以用数学归纳法证明
活动安排问题 算法分析 复杂度分析:为使最多的活动能相容地使用公共资源 • 若活动已按结束时间的非减序排列:算法只需O(n)的时间 • 若活动未按非减序排列:可以用O(nlogn)的时间先排序 全局最优解 • 贪心算法并不总能求得问题的整体最优解 • 但对于活动安排问题,贪心算法却总能求得的整体最优解 • 即:它最终所确定的相容活动集合A的规模最大 • 这个结论可以用数学归纳法证明
活动安排问题实例 例:设待安排的11个活动的开始时间和结束时间按 结束时间的非减序排列如下: 12 3 45 6 7 8 9 10 11 S[i] 1 3 0 5 3 5 6 8 8 2 12 f订 45 6 7 8 9 10 11 12 13 14
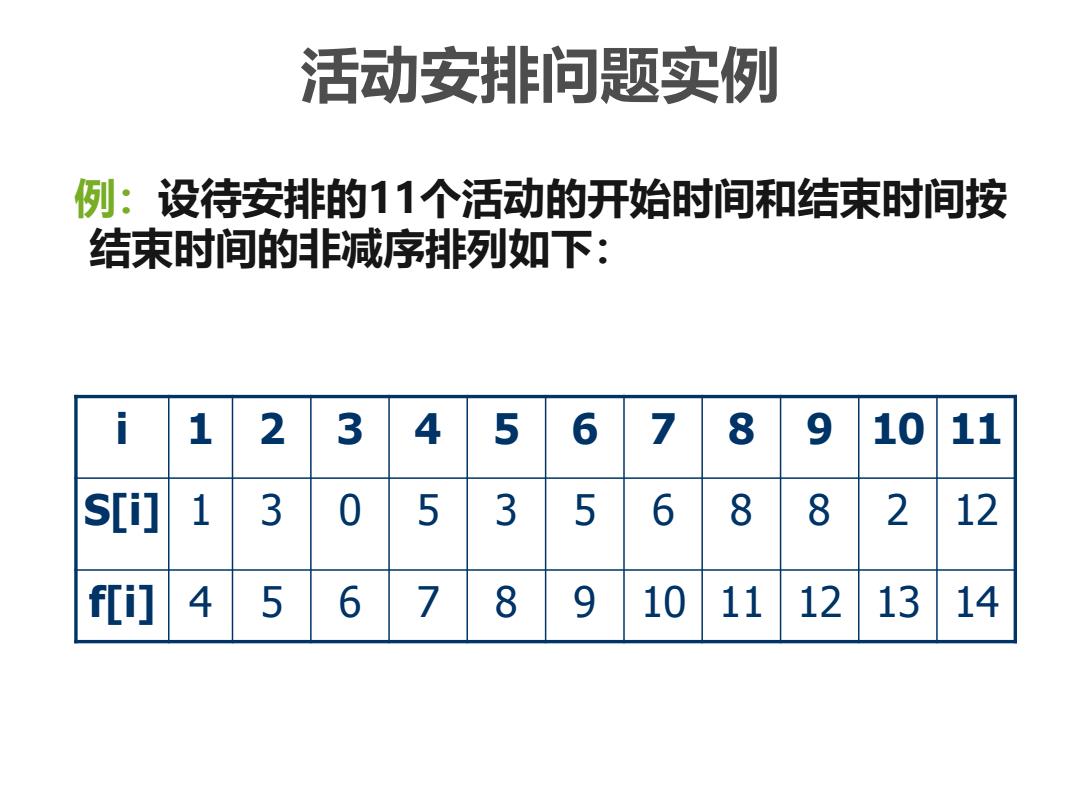
活动安排问题实例 例:设待安排的11个活动的开始时间和结束时间按 结束时间的非减序排列如下: i 1 2 3 4 5 6 7 8 9 10 11 S[i] 1 3 0 5 3 5 6 8 8 2 12 f[i] 4 5 6 7 8 9 10 11 12 13 14

活动安排问题实例 算法greedySelector的 计算过程如左图所示。 图中每行相应于算法的 一次迭代。阴影长条表 示的活动是已选入集合A 的活动,而空白长条表 示的活动是当前正在检 查相容性的活动。 01234567891011121314
活动安排问题实例 算 法 greedySelector 的 计算过程如左图所示。 图中每行相应于算法的 一次迭代。阴影长条表 示的活动是已选入集合A 的活动,而空白长条表 示的活动是当前正在检 查相容性的活动

4.2贪心算法的基本要素
4.2 贪心算法的基本要素