
贪心算法与动态规划的区别 @R 动态规划算法 Φ每一步的最优解是由上一步的局部最优解进行选择得到的 因此需要保存(之前求解的)所有子问题的最优解备查 3 贪心算法 贪心策略:下一步的最优解是由上一步的最优解推导得到的 当前最优解包含上一步的最优解,之前的最优解则不作保留 因此在贪心算法中作出的每步决策都无法改变(不能回退) 3 二者关系 贪心算法本质上是一种(更快的) 动态规划算法 贪心法正确的条件:每一步的最优解一定包含上一步的最优解 如果可以证明:在递归求解的每一步,按贪心选择策略选出的 局部最优解,最终可导致全局最优解,则二者是等价的
贪心算法与动态规划的区别 动态规划算法 每一步的最优解是由上一步的局部最优解进行选择得到的 因此需要保存(之前求解的)所有子问题的最优解备查 贪心算法 贪心策略:下一步的最优解是由上一步的最优解推导得到的 当前最优解包含上一步的最优解,之前的最优解则不作保留 因此在贪心算法中作出的每步决策都无法改变(不能回退) 二者关系 贪心算法本质上是一种(更快的)动态规划算法 贪心法正确的条件:每一步的最优解一定包含上一步的最优解 如果可以证明:在递归求解的每一步,按贪心选择策略选出的 局部最优解,最终可导致全局最优解,则二者是等价的
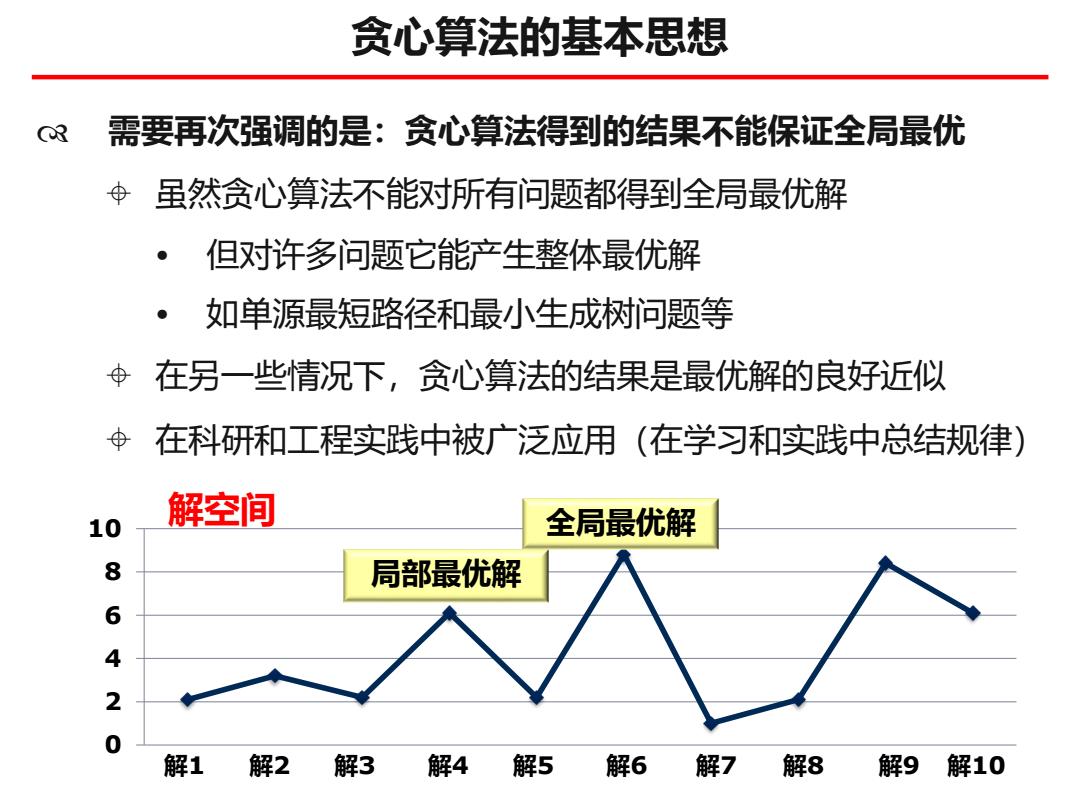
贪心算法的基本思想 C8 需要再次强调的是:贪心算法得到的结果不能保证全局最优 虽然贪心算法不能对所有问题都得到全局最优解 但对许多问题它能产生整体最优解 。1 如单源最短路径和最小生成树问题等 在另一些情况下,贪心算法的结果是最优解的良好近似 在科研和工程实践中被广泛应用(在学习和实践中总结规律) 解空间 10 全局最优解 8 局部最优解 2 解1解2 解3 解4 解5 解6解7 解8 解9解10
贪心算法的基本思想 需要再次强调的是:贪心算法得到的结果不能保证全局最优 虽然贪心算法不能对所有问题都得到全局最优解 • 但对许多问题它能产生整体最优解 • 如单源最短路径和最小生成树问题等 在另一些情况下,贪心算法的结果是最优解的良好近似 在科研和工程实践中被广泛应用(在学习和实践中总结规律) 0 2 4 6 8 10 解空间 解1 解2 解3 解4 解5 解6 解7 解8 解9 解10 局部最优解 全局最优解

4.1活动安排问题 Activity-Selection Problem)
4.1 活动安排问题 ( Activity-Selection Problem)

活动安排问题 0R 问题定义 Φ设:有n个活动的集合E={1,2,.,n} Φ其中:每个活动都要求竞争使用同一资源 (如演讲会场等), 而在同一时间内只有一个活动能使用这一资源 每个活动1都有一个请求使用该资源的起始时间S: 每个活动i都有一个使用资源的结束时间f,且s,<f: 如果选择了活动i,则它在半开时间区间[s,f)内占用资源 若区间[S,f)与S,f)不相交,则称活动i与活动是相容的 也就是说,当S;≥f或S≥f时,活动i与活动j相容 活动安排问题就是要在所给的活动集合中,选出最大的相容活 动子集合,即使得尽可能多的活动能兼容地使用公共资源
活动安排问题 问题定义 设:有n个活动的集合E={1,2,…,n} 其中:每个活动都要求竞争使用同一资源(如演讲会场等), 而在同一时间内只有一个活动能使用这一资源 • 每个活动 i 都有一个请求使用该资源的起始时间 si • 每个活动 i 都有一个使用资源的结束时间 fi,且 si < fi • 如果选择了活动 i,则它在半开时间区间[si , fi)内占用资源 • 若区间[si , fi )与[sj , fj )不相交,则称活动i与活动j是相容的 • 也就是说,当 si ≥ fj 或 sj≥fi 时,活动i与活动j相容 活动安排问题就是要在所给的活动集合中,选出最大的相容活 动子集合,即使得尽可能多的活动能兼容地使用公共资源
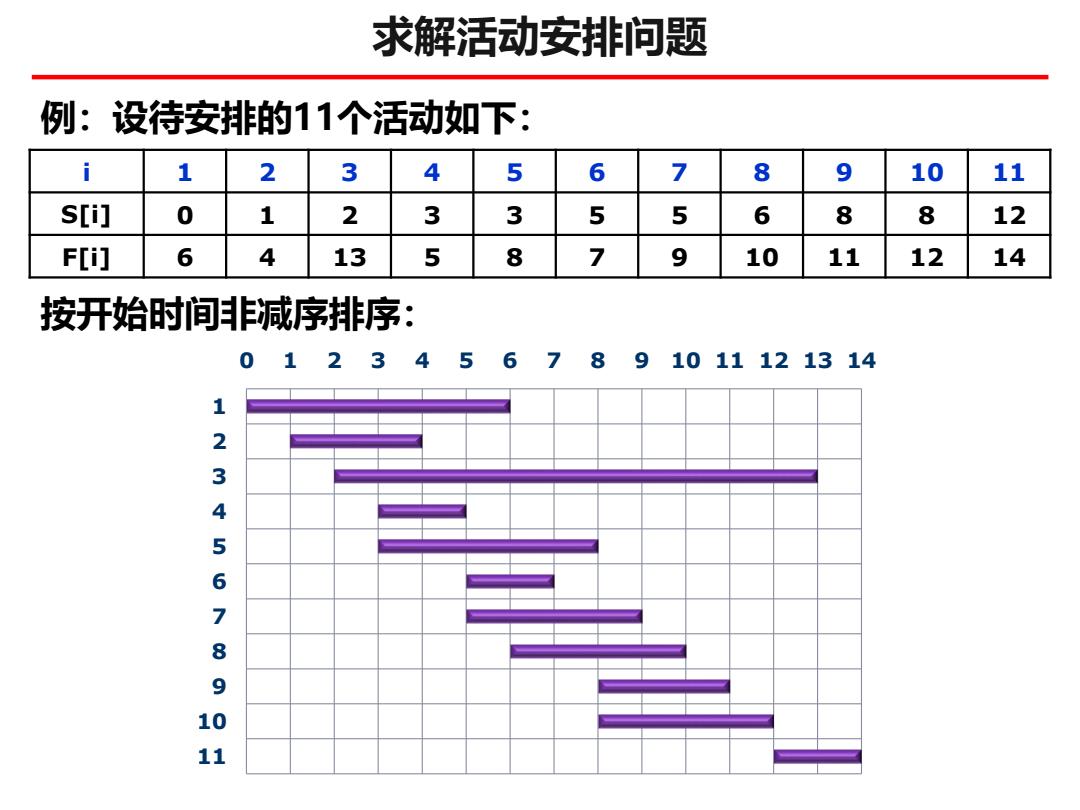
求解活动安排问题 例:设待安排的11个活动如下: i 1 2 3 4 5 6 7 8 9 10 11 S[i] 0 1 2 3 3 5 5 6 8 8 12 Fti] 6 4 13 5 8 7 9 10 11 12 14 按开始时间非减序排序: 01234567891011121314 1 2 3 4 5 6 7 8 9 10
求解活动安排问题 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1 2 3 4 5 6 7 8 9 10 11 例:设待安排的11个活动如下: i 1 2 3 4 5 6 7 8 9 10 11 S[i] 0 1 2 3 3 5 5 6 8 8 12 F[i] 6 4 13 5 8 7 9 10 11 12 14 按开始时间非减序排序: