
内喜古科私大举 ◆比例调节的特点 (1)作用快 (2)有余差(静差) 对于某一给定系统,当负荷变化时,静差的大小与比 例带(P)有关,P愈大,静差愈大:P愈小,静差愈小。 (3)比例带(P) 12
12 ◆比例调节的特点 (1)作用快 (2)有余差(静差) 对于某一给定系统,当负荷变化时,静差的大小与比 例带(P)有关,P愈大,静差愈大;P愈小,静差愈小。 (3)比例带(P )

窗山麦古科私大拳 在工业上,比例调节器比例作用的强弱常用比例带P(有时 又称“比例度δ”,P的宽窄即是表示比例度δ的大小)来表 示。 比例度δ的定义如下: 8=H-H,)/Zm-乙m×100% (P-R)(Pnmx-Pnmn) △e(Z-Zm×100% △e=H-H。—调节器的输入偏差; Ap/(P-Prin) △P=P-P。一调节器的相应输出变化; Z-Zn一调节器输入的变化范围即仪表的量程: P.-P。一调节器输出的变化范围。 13
13 在工业上,比例调节器比例作用的强弱常用比例带P(有时 又称“比例度δ”,P的宽窄即是表示比例度δ的大小)来表 示。 比例度δ的定义如下: 100% /( ) /( ) 100% ( )/( ) ( )/( ) max min max min 0 max min 0 max min − − = − − − − = P P P e Z Z P P P P H H Z Z

δ代表使调节阀开度改变100%,即从全关到全开时所需要的被调量的变化范围。 只有当被调量处在这个范围以内,调节阀的开度(变化)才与偏差成比例, 比例度的名字也就由此而来的。超出这个“比例带”以外,调节阀已处于全 关或全开的状态,此时调节器的输出与输入已不再保持比例关系,而调节器 至少也暂时失去了其控制作用 实际上,调节器的比例带P习惯用它相对于被调量测量仪表的量程的百分 数表示,所以,比例度δ又可定义为:使调节器的输出变化达到全量程(或全 范围)时,输入偏差改变了满量程的百分比。例如,当δ=100%时,输入改 变了满量程的100%,则输出也能按比例地改变其全范围的100%;当δ=200 %时,输入要改变满量程的200%时,输出才能够改变全范围的100%;换句 话说,即当输入改变满量程的100%时,输出只能改变其全范围的50%。 可见,δ大则调节作用就弱,δ小则调节作用就强。 δ的大小也可以用比例带(P)的宽窄来表示:δ大则比例带(P)宽,δ小则比例 带(P)窄。 一般情况下,对于单元组合仪表来说,比例度δ与其放大倍数K互为倒数 关系,即: △U=Kn×△e=x△e 14
14 δ代表使调节阀开度改变100%,即从全关到全开时所需要的被调量的变化范围。 只有当被调量处在这个范围以内,调节阀的开度(变化)才与偏差成比例, 比例度的名字也就由此而来的。超出这个“比例带”以外,调节阀已处于全 关或全开的状态,此时调节器的输出与输入已不再保持比例关系,而调节器 至少也暂时失去了其控制作用 实际上,调节器的比例带P习惯用它相对于被调量测量仪表的量程的百分 数表示,所以,比例度δ又可定义为:使调节器的输出变化达到全量程(或全 范围)时,输入偏差改变了满量程的百分比。例如,当δ=100%时,输入改 变了满量程的100%,则输出也能按比例地改变其全范围的100%;当δ=200 %时,输入要改变满量程的200%时,输出才能够改变全范围的100%;换句 话说,即当输入改变满量程的100%时,输出只能改变其全范围的50%。 可见,δ大则调节作用就弱,δ小则调节作用就强。 δ的大小也可以用比例带(P)的宽窄来表示:δ大则比例带(P)宽,δ小则比例 带(P)窄。 一般情况下,对于单元组合仪表来说,比例度δ与其放大倍数Kp互为倒数 关系,即: U K e e = p = 1
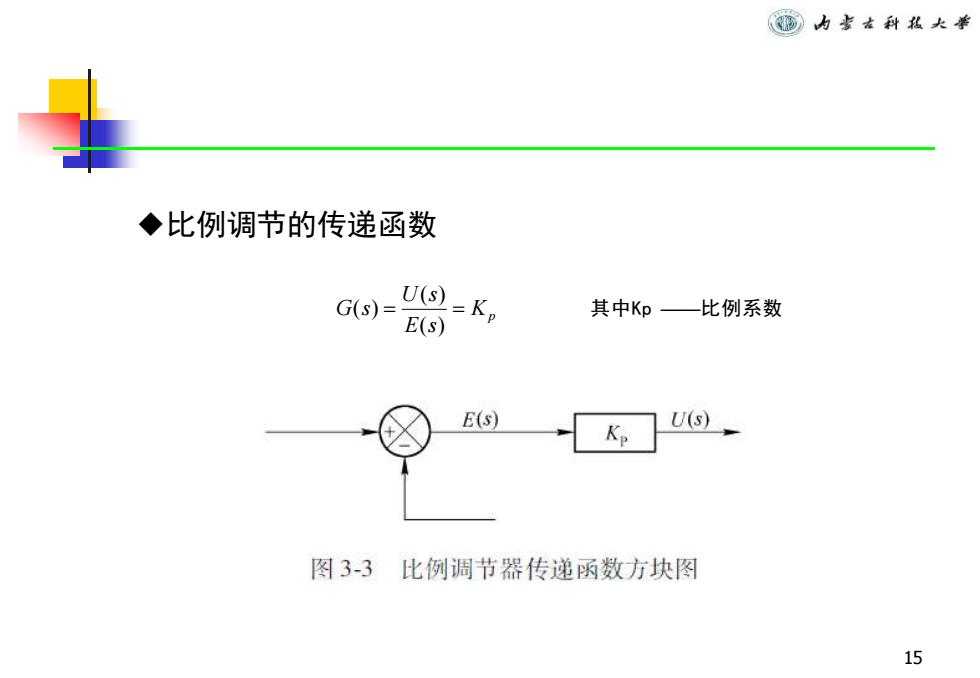
窗内害古科私大举 ◆比例调节的传递函数 G(s)= Us=K。 其中Kp— 比例系数 E(s) E(s) U(s) 图3-3 比例调节器传递函数方块图 15
15 ◆比例调节的传递函数 Kp E s U s G s = = ( ) ( ) ( ) 其中Kp ——比例系数

内喜古科私大幸 ●积分(①调节规律 ◆积分调节规律 ◆积分时间 ◆积分调节的特点 ◆积分调节的传递函数 16
16 ●积分(I)调节规律 ◆积分调节规律 ◆ 积分时间 ◆积分调节的特点 ◆积分调节的传递函数