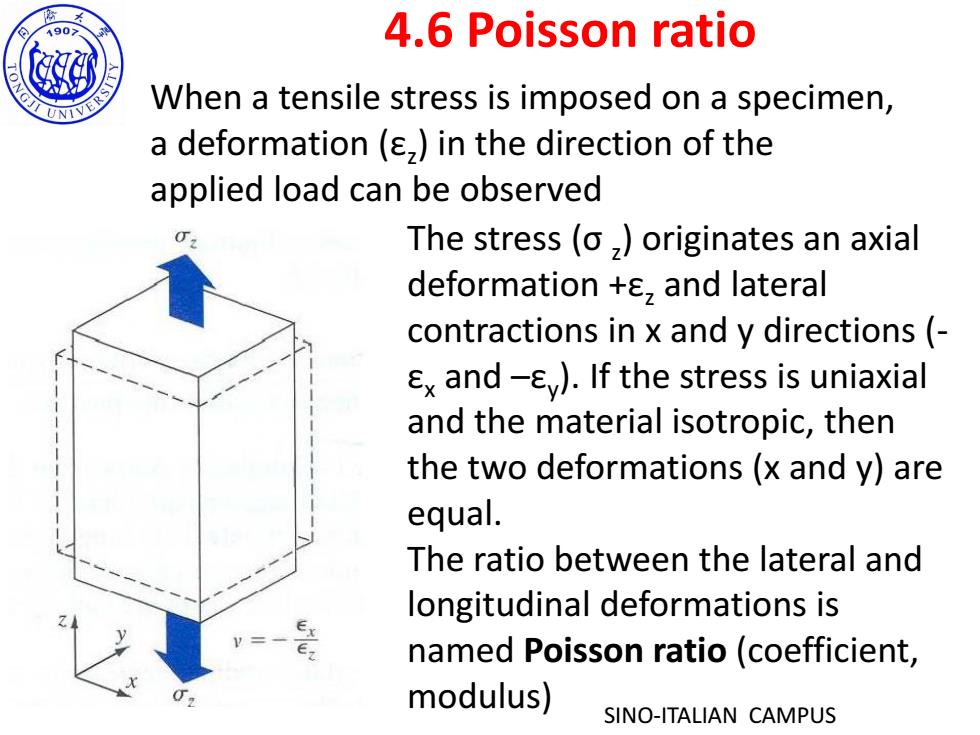
190> 4.6 Poisson ratio When a tensile stress is imposed on a specimen, a deformation(,)in the direction of the applied load can be observed The stress(o,)originates an axial deformation +8,and lateral contractions in x and y directions(- Ex and -)If the stress is uniaxial and the material isotropic,then the two deformations(x and y)are equal. The ratio between the lateral and longitudinal deformations is e named Poisson ratio(coefficient, modulus) SINO-ITALIAN CAMPUS
SINO-ITALIAN CAMPUS 4.6 Poisson ratio When a tensile stress is imposed on a specimen, a deformation (εz ) in the direction of the applied load can be observed The stress (σ z ) originates an axial deformation +εz and lateral contractions in x and y directions (- εx and –εy ). If the stress is uniaxial and the material isotropic, then the two deformations (x and y) are equal. The ratio between the lateral and longitudinal deformations is named Poisson ratio (coefficient, modulus)

190> Cubic sample with no volume variation associated to tensile △I =2 - 10 5 △I 4 2 14 10 5 a0=10 8 0,5 &1 2 5 The maximum value (ideal materials)of the Poisson ratio is 0,5.Generally it ranges between 0,25 and 0,4 SINO-ITALIAN CAMPUS
SINO-ITALIAN CAMPUS Cubic sample with no volume variation associated to tensile The maximum value (ideal materials) of the Poisson ratio is 0,5. Generally it ranges between 0,25 and 0,4
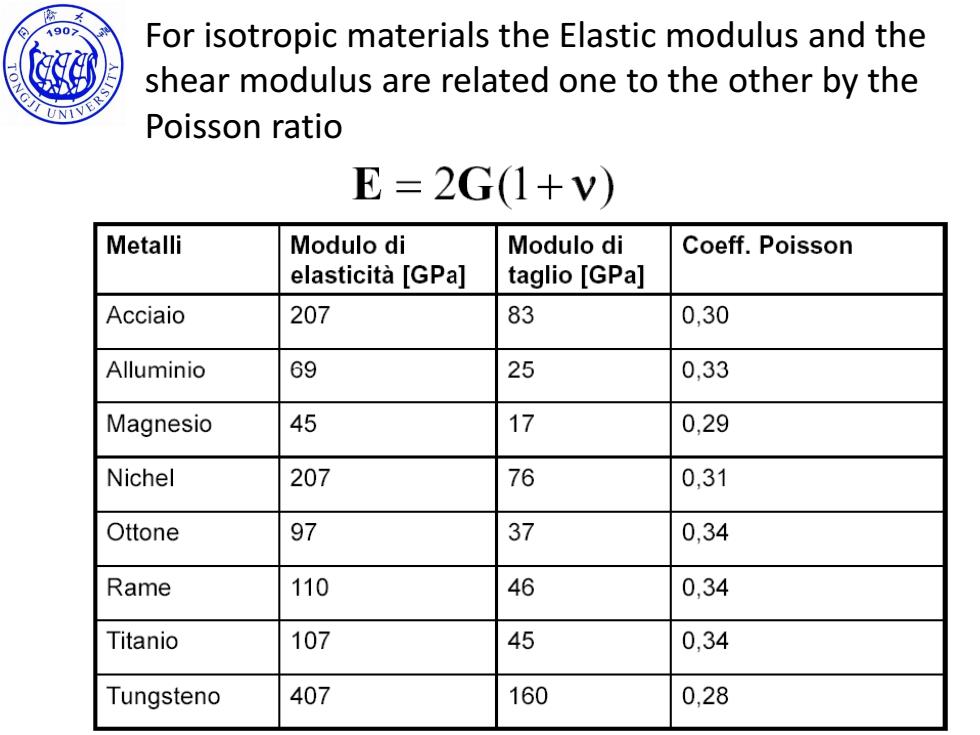
490> For isotropic materials the Elastic modulus and the TONGJI UNIVERS shear modulus are related one to the other by the Poisson ratio E=2G(1+V) Metalli Modulo di Modulo di Coeff.Poisson elasticita [GPa] taglio [GPa] Acciaio 207 83 0,30 Alluminio 69 25 0,33 Magnesio 45 17 0,29 Nichel 207 76 0,31 Ottone 97 37 0,34 Rame 110 46 0,34 Titanio 107 45 0.34 Tungsteno 407 160 0,28
SINO-ITALIAN CAMPUS For isotropic materials the Elastic modulus and the shear modulus are related one to the other by the Poisson ratio
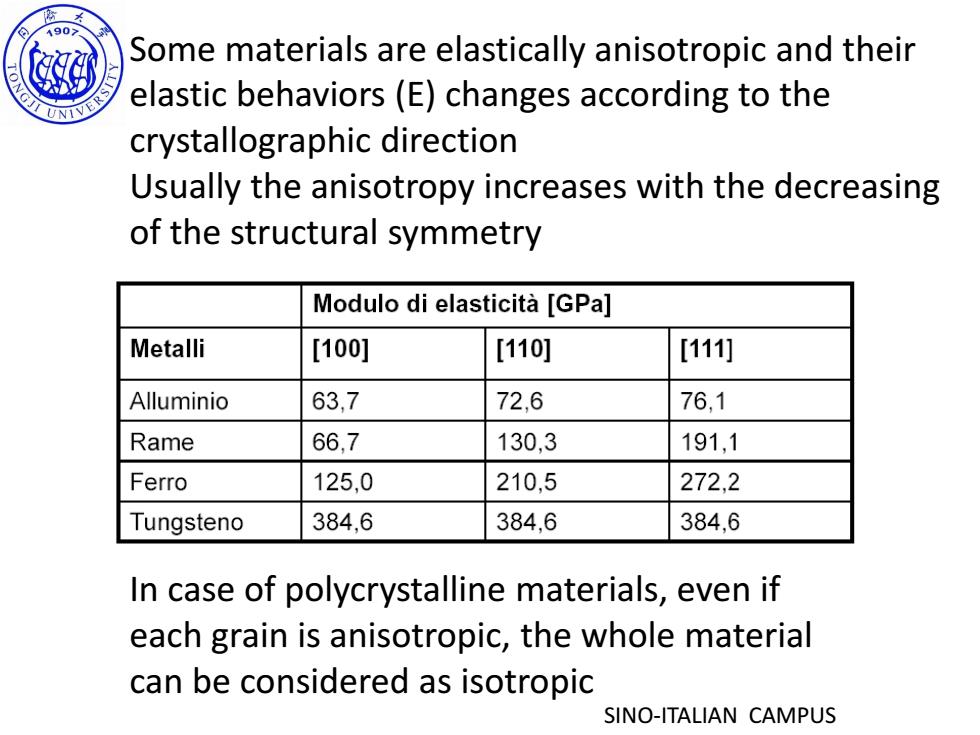
90> Some materials are elastically anisotropic and their elastic behaviors(E)changes according to the crystallographic direction Usually the anisotropy increases with the decreasing of the structural symmetry Modulo di elasticita [GPa] Metalli [100] [110] [111] Alluminio 63,7 72,6 76,1 Rame 66,7 130,3 191,1 Ferro 125,0 210,5 272,2 Tungsteno 384,6 384,6 384,6 In case of polycrystalline materials,even if each grain is anisotropic,the whole material can be considered as isotropic SINO-ITALIAN CAMPUS
SINO-ITALIAN CAMPUS Some materials are elastically anisotropic and their elastic behaviors (E) changes according to the crystallographic direction Usually the anisotropy increases with the decreasing of the structural symmetry In case of polycrystalline materials, even if each grain is anisotropic, the whole material can be considered as isotropic

190> A Cu specimen having initial length 305mm undergoes a tensile stress of 276MPa. If the deformation is totally elastic,which is going to be the resulting elongation?The value of E for Cu is 110GPa. Purely elastic deformation: o=E8 Elongation is expressed through: £= -L。-△l Combining the equations: o=EE= ()EA1= Using the given values: Al-(276MPa)(305mm)-0.77mm 110-103MPa SINO-ITALIAN CAMPUS
SINO-ITALIAN CAMPUS A Cu specimen having initial length 305mm undergoes a tensile stress of 276MPa. If the deformation is totally elastic, which is going to be the resulting elongation? The value of E for Cu is 110GPa. Purely elastic deformation: 𝜎 = 𝐸𝜀 Elongation is expressed through: 𝜀 = 𝑙𝑙−𝑙 0 𝑙 0 = ∆𝑙 𝑙 0 Combining the equations: 𝜎 = 𝐸𝜀 = ∆𝑙 𝑙 0 E ∆𝑙= 𝜎𝑙 0 𝐸 Using the given values: ∆𝑙= (276𝑀𝑃𝑎)(305𝑚𝑚) 110·103MPa =0.77mm