
Stack操作部分的形式约束 initialise(s) pre true (none * post elems'={} (elems'is an empty set * push(s,a) pre lelemsl<max (s is not full * post c>c and (a,c)E elems' (the new time-stamp c'is larger than the previous time-stamp c'and the pair (a,c)belong to S*)
Stack操作部分的形式约束

Stacki操作部分的形式约束 pop(s) pre lelems>0 (s is not empty * post 3(a,b)E elems such that (*(a,b)is the element in s with largest [v(p,q)∈elems b≥ql time-stamp b and is deleted from and elems'=elems-{(a,b)} elems * top(s) pre lelemsl>0 post :3(a,b)E elems such that (*(a,b)is the element in S with [∀(p,q)∈elems b≥g] largest time-stamp b and a is and top(s)=a returned as the value of the function.Note that c and s are not changed *
Stack操作部分的形式约束

Stacki操作部分的形式约束 empty(s) pre true post empty(s)=(l elemsl =0) full(s) pre true post full(s)=(l elemsl max) 这些数据规约和操作规约明确了这个数据结构的: 成员数据类型、组织方式、使用方式 但这些规约和具体的数据结构实现无关:数组方式?链表方式? 实现这个ADT时:必须验证实现方法保持了这些约束的成立
Stack操作部分的形式约束 这些数据规约和操作规约明确了这个数据结构的: 成员数据类型、组织方式、使用方式 但这些规约和具体的数据结构实现无关:数组方式?链表方式? 实现这个ADT时:必须验证实现方法保持了这些约束的成立

以定义ADT为目标去定义数据结构的好处: ·关注分离 ·信息隐藏 ·模块化设计 ·可以加载形式化研究
以定义ADT为目标去定义数据结构的好处: • 关注分离 • 信息隐藏 • 模块化设计 • 可以加载形式化研究
两种用途非常广泛的特殊St:队列、栈 it is worthwhile,at least for reasons of algorithmic clarity,to think of queues and stacks as being in themselves data structures,rather than being merely special kinds of lists. in out in out back front Queue Stack a FIFO list(First-In-First-Out) a LIFO list (Last-In-First-Out) Specially devised elementary instructions such as 'add X to queue 4,"or push X on stack s,"rather than obscure formulations that explicitly involve indices
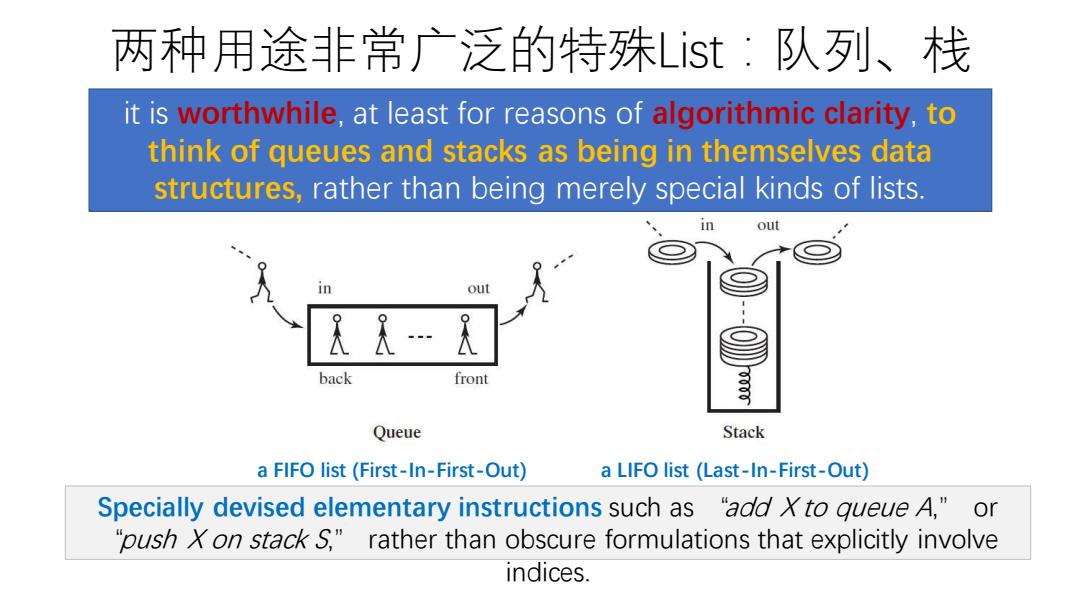
两种用途非常广泛的特殊List:队列、栈 a FIFO list (First-In-First-Out) a LIFO list (Last-In-First-Out) it is worthwhile, at least for reasons of algorithmic clarity, to think of queues and stacks as being in themselves data structures, rather than being merely special kinds of lists. Specially devised elementary instructions such as “add X to queue A,” or “push X on stack S,” rather than obscure formulations that explicitly involve indices