
版权所有:华东理工大学物理化学教研室 16 Example - Deriving a thermodynamic relation Show thermodynamically that πT = 0 for a perfect gas, and compute its value for a van der Waals gas Method: Proving a result 'thermodynamically' means basing it entirely on general thermodynamic relations and equations of state. Answer: 1). For a perfect gas, pV = nRT, and (∂p ∂T )V = nR / V From the equation of p Tp T V T ⎟ − ⎠⎞ ⎜⎝⎛ ∂∂ π = = − p = 0 VnRT πT
版权所有:华东理工大学物理化学教研室 16 Example - Deriving a thermodynamic relation Show thermodynamically that πT = 0 for a perfect gas, and compute its value for a van der Waals gas Method: Proving a result 'thermodynamically' means basing it entirely on general thermodynamic relations and equations of state. Answer: 1). For a perfect gas, pV = nRT, and (∂p ∂T )V = nR / V From the equation of p Tp T V T ⎟ − ⎠⎞ ⎜⎝⎛ ∂∂ π = = − p = 0 VnRT πT
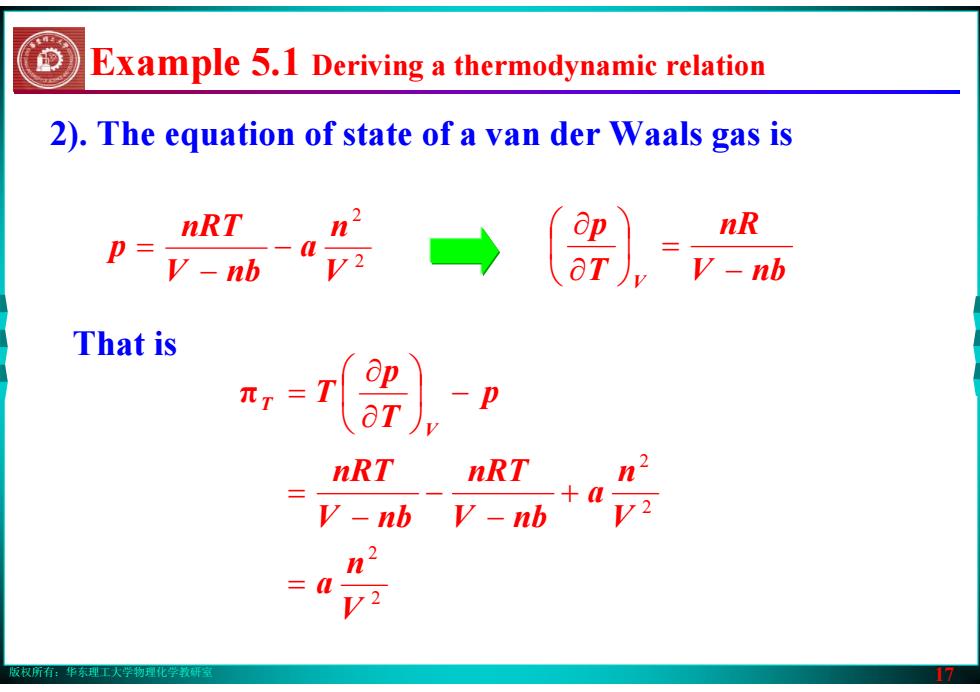
版权所有:华东理工大学物理化学教研室 17 2). The equation of state of a van der Waals gas is That is 2 2 2 2 V n a V n a V nb nRT V nb nRT p Tp T V T = + − − − = ⎟ − ⎠⎞ ⎜⎝⎛ ∂∂ π = 2 2 V n a V nb nRT p − − = V nb nR T p V − ⎟ = ⎠⎞ ⎜⎝⎛ ∂∂ Example 5.1 Deriving a thermodynamic relation
版权所有:华东理工大学物理化学教研室 17 2). The equation of state of a van der Waals gas is That is 2 2 2 2 V n a V n a V nb nRT V nb nRT p Tp T V T = + − − − = ⎟ − ⎠⎞ ⎜⎝⎛ ∂∂ π = 2 2 V n a V nb nRT p − − = V nb nR T p V − ⎟ = ⎠⎞ ⎜⎝⎛ ∂∂ Example 5.1 Deriving a thermodynamic relation

版权所有:华东理工大学物理化学教研室 18 Combing the First and Second Laws 5.1 Properties of the internal energy 5.2 Properties of the Gibbs energy 5.3 The chemical potential of a pure substance Real gases:the fugacity 5.4 The definition of fugacity 5.5 Standard states of real gases 5.6 The relation between fugacity and pressure 5. The Second Law: the machinery
版权所有:华东理工大学物理化学教研室 18 Combing the First and Second Laws 5.1 Properties of the internal energy 5.2 Properties of the Gibbs energy 5.3 The chemical potential of a pure substance Real gases:the fugacity 5.4 The definition of fugacity 5.5 Standard states of real gases 5.6 The relation between fugacity and pressure 5. The Second Law: the machinery

版权所有:华东理工大学物理化学教研室 19 dG = Vdp − SdT For a closed system doing non-expansion work and at constant composition G = G( p,T ) p T p S T V ⎟⎟⎠⎞ ⎜⎜⎝⎛ ∂∂ ⎟ = − ⎠⎞ ⎜⎝⎛ ∂∂ S T G V p G T p ⎟ = − ⎠⎞ ⎜⎝⎛ ∂∂ = ⎟⎟⎠⎞ ⎜⎜⎝⎛ ∂∂ , 1). The outline of the Gibbs energy with T and p 5.2 Properties of the Gibbs energy
版权所有:华东理工大学物理化学教研室 19 dG = Vdp − SdT For a closed system doing non-expansion work and at constant composition G = G( p,T ) p T p S T V ⎟⎟⎠⎞ ⎜⎜⎝⎛ ∂∂ ⎟ = − ⎠⎞ ⎜⎝⎛ ∂∂ S T G V p G T p ⎟ = − ⎠⎞ ⎜⎝⎛ ∂∂ = ⎟⎟⎠⎞ ⎜⎜⎝⎛ ∂∂ , 1). The outline of the Gibbs energy with T and p 5.2 Properties of the Gibbs energy

版权所有:华东理工大学物理化学教研室 20 The entropy of the gaseous phase of a substance is greater than that of the liquid phase, and the entropy of the solid phase is smallest, the Gibbs energy changes most steeply for the gas phase, followed by the liquid phase, and then the solid phase of the substance. The variation of the Gibbs energy with the temperature is determined by the entropy G = G( p,T ) dG = Vdp − SdT 1). The outline of the Gibbs energy with T and p S T G p ⎟ = − ⎠⎞ ⎜⎝⎛ ∂∂ 5.2 Properties of the Gibbs energy
版权所有:华东理工大学物理化学教研室 20 The entropy of the gaseous phase of a substance is greater than that of the liquid phase, and the entropy of the solid phase is smallest, the Gibbs energy changes most steeply for the gas phase, followed by the liquid phase, and then the solid phase of the substance. The variation of the Gibbs energy with the temperature is determined by the entropy G = G( p,T ) dG = Vdp − SdT 1). The outline of the Gibbs energy with T and p S T G p ⎟ = − ⎠⎞ ⎜⎝⎛ ∂∂ 5.2 Properties of the Gibbs energy