杭州电子科技大学：《大学物理》课程实验指导（基础物理）实验25 电子束的偏转与聚焦及电子荷质比的测定

实验25电子荷质比的测量 【实验目的】 1.了解电子在电场和磁场中的运动规律： 2.学习用磁聚焦法测量电子的荷质比： 3.通过本实验加深对洛伦兹力的认识。 【实验仪器】 DZS-D型电子束实验仪 【实验原理】 1,示波管的简单介绍： 示波管如图1所示，示波管包括有： (1)一个电子枪，它发射电子，把电子加速到一定速度，并聚焦成电子束： (2)一个由两对金属板组成的偏转系统： (3)一个在管子末端的荧光屏，用来显示电子束的轰击点。 水年转 酸者限我狂桥 光所 电子枪 图1小型示波管外形示意图 所有部件全都密封在一个抽成真空的玻璃外壳里，目的是为了避免电子与气体分 子碰撞而引起电子束散射。接通电源后，灯丝发热，阴极发射电子。栅极加上相对于 阴极的负电压，它有两个作用：①一方面调节栅极电压的大小控制阴极发射电子的强 度，所以栅极也叫控制极：②另一方面栅极电压和第一阳极电压构成一定的空间电位 分布，使得由阴极发射的电子束在栅极附近形成一个交叉点。第一阳极和第二阳极的 作用一方面构成聚焦电场，使得经过第一交叉点又发散了的电子在聚焦场作用下又会 聚起来：另一方面使电子加速，电子以高速打在荧光屏上，屏上的荧光物质在高速电 子轰击下发出荧光，荧光屏上的发光亮度取决于到达荧光屏的电子数目和速度，改变 栅压及加速电压的大小都可控制光点的亮度。水平偏转板和垂直偏转板是互相垂直的 平行板，偏转板上加以不同的电压，用来控制荧光屏上亮点的位置。 2.电子的加速和电偏转： 为了描述电子的运动，我们选用了一个直角坐标系，其：轴沿示波管管轴，x轴 是示波管正面所在平面上的水平线，y轴是示波管正面所在平面上的竖直线。 从阴极发射出来通过电子枪各个小孔的一个电子，它在从阳极A,射出时在Z方向 上具有速度Vz:Vz的值取决于K和A,之间的电位差V2=V。+Vc(图2)。 电子从K移动到A2,位能降低了e·V2;因此，如果电子逸出阴极时的初始动能

1 实验 25 电子荷质比的测量 【实验目的】 1. 了解电子在电场和磁场中的运动规律； 2. 学习用磁聚焦法测量电子的荷质比； 3. 通过本实验加深对洛伦兹力的认识。 【实验仪器】 DZS D 型电子束实验仪 【实验原理】 1． 示波管的简单介绍： 示波管如图 1 所示，示波管包括有： （1）一个电子枪，它发射电子，把电子加速到一定速度，并聚焦成电子束； （2）一个由两对金属板组成的偏转系统； （3）一个在管子末端的荧光屏，用来显示电子束的轰击点。 图 1 小型示波管外形示意图 所有部件全都密封在一个抽成真空的玻璃外壳里，目的是为了避免电子与气体分 子碰撞而引起电子束散射。接通电源后，灯丝发热，阴极发射电子。栅极加上相对于 阴极的负电压，它有两个作用：①一方面调节栅极电压的大小控制阴极发射电子的强 度，所以栅极也叫控制极；②另一方面栅极电压和第一阳极电压构成一定的空间电位 分布，使得由阴极发射的电子束在栅极附近形成一个交叉点。第一阳极和第二阳极的 作用一方面构成聚焦电场，使得经过第一交叉点又发散了的电子在聚焦场作用下又会 聚起来；另一方面使电子加速，电子以高速打在荧光屏上，屏上的荧光物质在高速电 子轰击下发出荧光，荧光屏上的发光亮度取决于到达荧光屏的电子数目和速度，改变 栅压及加速电压的大小都可控制光点的亮度。水平偏转板和垂直偏转板是互相垂直的 平行板，偏转板上加以不同的电压，用来控制荧光屏上亮点的位置。 2．电子的加速和电偏转： 为了描述电子的运动，我们选用了一个直角坐标系，其 z 轴沿示波管管轴， x 轴 是示波管正面所在平面上的水平线， y 轴是示波管正面所在平面上的竖直线。 从阴极发射出来通过电子枪各个小孔的一个电子，它在从阳极 A2 射出时在 z 方向 上具有速度 Z v ； Z v 的值取决于 K 和 A2 之间的电位差 V2  VB  VC （图 2）。 电子从 K 移动到 A2 ，位能降低了 V2 e  ；因此，如果电子逸出阴极时的初始动能

可以忽略不计，那么它从A,射出时的动能二mV,2就由下式确定： G1 G2 A1 7mev:-c.V: ☑ 图2电子枪电极结构示意图 亮点。 是，如果两个垂直偏转板（水平放置的一对）之间加有电位差V。,使偏转板之间形成 一个横向电场E,那么作用在电子上的电场力便使电子获得一个横向速度V,但却 不改变它的轴向速度分量V,这样，电子在离开偏转板时运动的方向将与z轴成一个 夹角日，而这个0角由下式决定： g9= V 如图3 +++++++ 电的 尺寸，那么 以 上 荧光尿

2 可以忽略不计，那么它从 A2 射出时的动能 2 m vz 2 1  就由下式确定： 2 2 m vz e V 2 1    (1) 图 2 电子枪电极结构示意图 此后，电子再通过偏转板之间的空间。如果偏转板之间没有电位差，那么电子将 笔直地通过。最后打在荧光屏的中心（假定电子枪描准了中心）形成一个小亮点。但 是，如果两个垂直偏转板（水平放置的一对）之间加有电位差 Vd ，使偏转板之间形成 一个横向电场 Ey ，那么作用在电子上的电场力便使电子获得一个横向速度 vy ，但却 不改变它的轴向速度分量 z v ，这样，电子在离开偏转板时运动的方向将与 z 轴成一个 夹角 ，而这个 角由下式决定： z y v v tg  (2) 如 图 3 所 示。如 果知道了偏 转 电 位差和偏转 板 的 尺寸，那么 以 上

各个量都能计算出来。 图3电子在电场中的运动 设距离为d的两个偏转板之间的电位差V。在其中产生一个横向电场 E,=V。/d,从而对电子作用一个大小为F,=eE,=eV/d的横向力。在电子从 偏转板之间通过的时间△t内，这个力使电子得到一个横向动量v,而它等于力的 冲量，即 (3) 于是： v,-e.V.At (4) m d 然而，这个时间间隔△t,也就是电子以轴向速度V,通过距离1(1等于偏转板的长 度)所需要的时间，因此1=V,△1。由这个关系式解出At,代入冲量一动量关系式 结果得： (5) m d v. 这样，偏转角0就由下式给出： tg0=业=eVl (6) 配能显关系式)代入上式m 这个公式表明，偏转角随偏转电位差V的增加而增大，而且，偏转角也随偏转板 长度1的增大而增大，偏转角与成反比，对于给定的总电位差来说，两偏转板之间置 离越近，偏转电场就越强。最后，降低加速电位差V,三V。+V也能增大偏转，这是 因为这样就减小了电子的轴向速度，延长了偏转电场对电子的作用时间。此外，对于 相同的横向速度，轴向速度越小，得到的偏转角就越大。 电子束离开偏转区域以后便又沿一条直线行进，这条直线是电子离开偏转区域 的电了轨迹的线。这样，荧光屏上的亮点会偏移一个直距高D,而这个距 关系式D=Lg0确定：这里L是偏转板到荧光屏的距离（忽略荧光屏的微小的曲率）

3 各个量都能计算出来。 图 3 电子在电场中的运动 设距离为 d 的两个偏转板之间的电位差 Vd 在其中产生一个横向电场 Ey  Vd / d ，从而对电子作用一个大小为 Fy  eEy  eVd / d 的横向力。在电子从 偏转板之间通过的时间 t 内，这个力使电子得到一个横向动量 mvy ，而它等于力的 冲量，即 d t m vy Fy t e Vd         (3) 于是： t d V m e v d y     (4) 然而，这个时间间隔 t ，也就是电子以轴向速度 z v 通过距离l (l 等于偏转板的长 度）所需要的时间，因此l v t  z 。 由这个关系式解出 t ，代入冲量一动量关系式 结果得： z d y v l d V m e v    (5) 这样，偏转角 就由下式给出： 2 z d z y d m v e V l v v tg        (6) 再把能量关系式（1）代入上式，最后得到： 2d l V V tg 2 d    (7) 这个公式表明，偏转角随偏转电位差 Vd 的增加而增大，而且，偏转角也随偏转板 长度l 的增大而增大，偏转角与d 成反比，对于给定的总电位差来说，两偏转板之间距 离越近，偏转电场就越强。最后，降低加速电位差 V2  VB  VC也能增大偏转，这是 因为这样就减小了电子的轴向速度，延长了偏转电场对电子的作用时间。此外，对于 相同的横向速度，轴向速度越小，得到的偏转角就越大。 电子束离开偏转区域以后便又沿一条直线行进，这条直线是电子离开偏转区域 那 一点的电子轨迹的切线。这样，荧光屏上的亮点会偏移一个垂直距离 D ，而这个距离 由 关系式 D  Ltg确定；这里 L 是偏转板到荧光屏的距离（忽略荧光屏的微小的曲率）

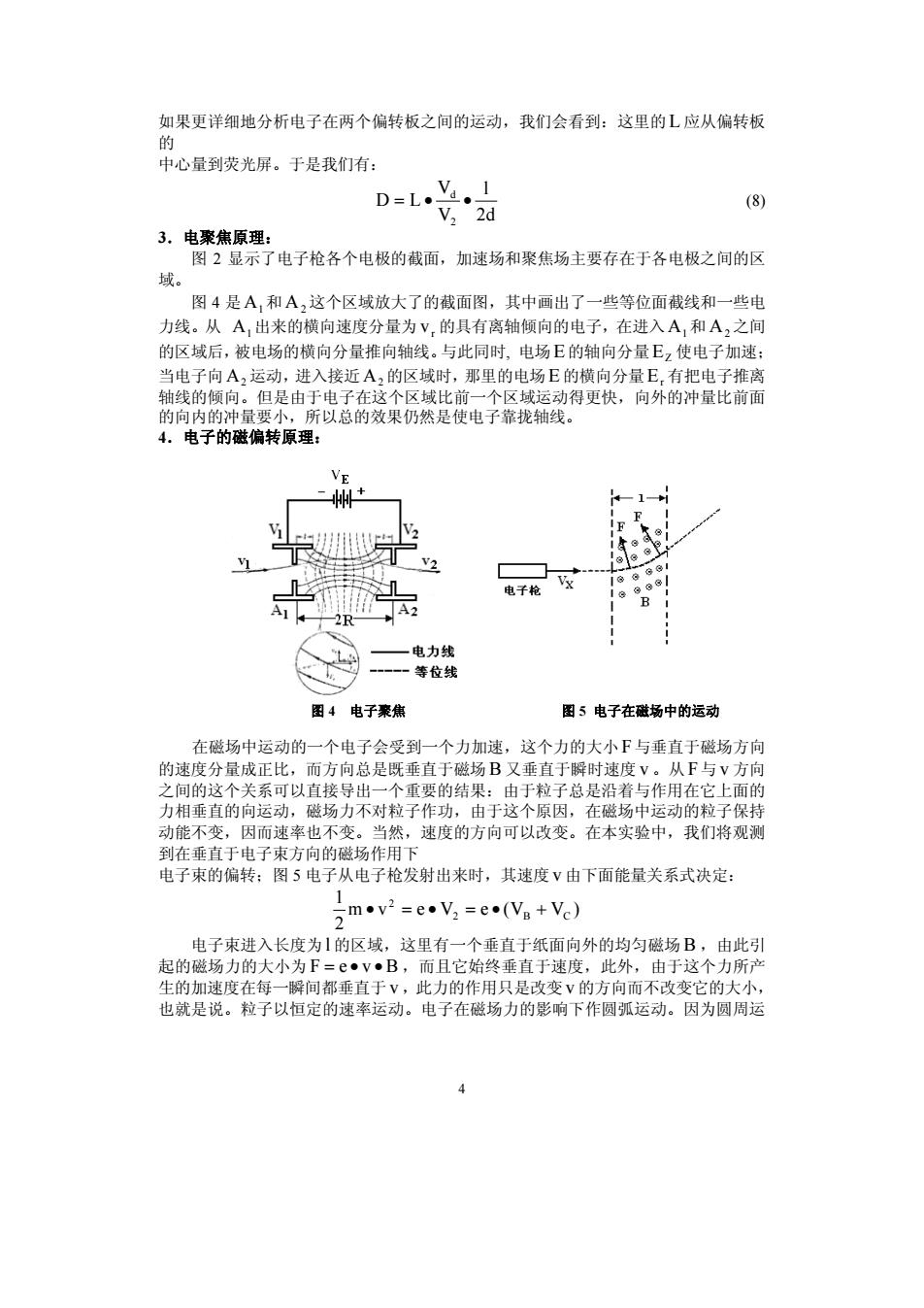
如果更详细地分析电子在两个偏转板之间的运动，我们会看到：这里的L应从偏转板 中心量到荧光屏。于是我们有： =1 © 3.电聚焦原理 图2显示了电子枪各个电极的截面，加速场和聚焦场主要存在于各电极之间的区 。 图4是A,和A,这个区域放大了的截面图，其中画出了一些等位面截线和一些电 力线。从A,出来的楷向速度分量为V的且有离轴面向的申子，在讲入A和A,之间 的区域后，被电场的横向分量推向轴线。与此同时，电场E的轴向分量E2使电子加速 当电子向A,运动，进入接近A,的区域时，那里的电场E的横向分量E,有把电子推密 动得更快，向外的冲量比前面 电子的磁偏转原理： 州 2 电子枪 A -2R- A2 图4电子豪焦 图5电子在磁场中的运动 在磁场中运动的一个电子会受到一个力加速，这个力的大小F与垂直于磁场方向 的速度分量成正比，而方向总是既垂直于磁场B又垂直于瞬时速度V。从F与V方向 之间的这个关系可以直接导出一个重要的结果：由于粒子总是沿若与作用在它上面的 力相垂直的向运动，磁场力不对粒子作功，由于这个原因，在磁场中运动的粒子保持 动能不变，因而速率也不变。当然，速度的方向可以改变。在本实验中，我们将观测 到在垂直于电子束方向的磁场作用下 电子束的偏转：图5电子从电子枪发射出来时，其速度V由下面能量关系式决定： mv2=eV2=e.(Va+Vc) 电子束进入长度为1的区域，这里有一个垂直于纸面向外的均匀磁场B,由此引 起的磁场力的大小为F=eV·B,而且它始终垂直于速度，此外，由于这个力所产 生的加速度在每一瞬间都垂直于V,此力的作用只是改变V的方向而不改变它的大小 也就是说。粒子以恒定的速率运动。电子在磁场力的影响下作圆弧运动。因为圆周运 4

4 如果更详细地分析电子在两个偏转板之间的运动，我们会看到：这里的 L 应从偏转板 的 中心量到荧光屏。于是我们有： 2d l V V D L 2 d    (8) 3．电聚焦原理： 图 2 显示了电子枪各个电极的截面，加速场和聚焦场主要存在于各电极之间的区 域。 图 4 是 A1和 A2这个区域放大了的截面图，其中画出了一些等位面截线和一些电 力线。从 A1出来的横向速度分量为 r v 的具有离轴倾向的电子，在进入 A1和 A2之间 的区域后，被电场的横向分量推向轴线。与此同时, 电场E 的轴向分量 EZ 使电子加速； 当电子向 A2 运动，进入接近 A2的区域时，那里的电场 E 的横向分量 Er 有把电子推离 轴线的倾向。但是由于电子在这个区域比前一个区域运动得更快，向外的冲量比前面 的向内的冲量要小，所以总的效果仍然是使电子靠拢轴线。 4．电子的磁偏转原理： 图 4 电子聚焦 图 5 电子在磁场中的运动 在磁场中运动的一个电子会受到一个力加速，这个力的大小 F与垂直于磁场方向 的速度分量成正比，而方向总是既垂直于磁场 B 又垂直于瞬时速度 v 。从 F与 v 方向 之间的这个关系可以直接导出一个重要的结果：由于粒子总是沿着与作用在它上面的 力相垂直的向运动，磁场力不对粒子作功，由于这个原因，在磁场中运动的粒子保持 动能不变，因而速率也不变。当然，速度的方向可以改变。在本实验中，我们将观测 到在垂直于电子束方向的磁场作用下 电子束的偏转；图 5 电子从电子枪发射出来时，其速度 v 由下面能量关系式决定： m v e V e (V V ) 2 1 2 B C 2       电子束进入长度为 l 的区域，这里有一个垂直于纸面向外的均匀磁场 B ，由此引 起的磁场力的大小为 F  e  v B ，而且它始终垂直于速度，此外，由于这个力所产 生的加速度在每一瞬间都垂直于 v ，此力的作用只是改变 v 的方向而不改变它的大小， 也就是说。粒子以恒定的速率运动。电子在磁场力的影响下作圆弧运动。因为圆周运

动的向心加速为v2/R,而产生这个加速度的力（有时称为向心力）必定为m·v2/R, 所以圆弧的半径很容易计算出来。向心力等于F=ev·B,因而 ·点相对于没有偏转的电子束的位置移动了 段距离。 5.磁聚焦和电子荷质比的测量原理： 置于长直螺线管中的示波管，在不受任何偏转电压的情况下，示波管正常工作时， 调节亮度和聚焦，可在荧光屏上得到一个小亮点。若第二加速阳极A,的电压为V, 则电子的轴向运动速度用V,表示，则有 e.V, v,-m (9 当给其中一对偏转板加上交变电压时，电子将获得垂直于轴向的分速度（用V,表 示)，此时荧光屏上便出现一条直线，随后给长直螺线管通一直流电流I,于是螺线管 内便产生磁场，其磁场感应强度用B表示。众所周知，运动电子在磁场中要受到罗伦 磁力F=v,B的作用(V,方向受力为零)，这个力使电子在垂直于磁场（也垂直于螺 线管轴线)的平面内作园周运动，设其园周运动的半径为R,则有： e,B=my即R=mg R e●B 0) 圆周运动的周期为： T=2πR2x·m (11) c.B 电子既在轴线方面作直线运动，又在垂直于轴线的平面内作园周运动。它的轨道 是一条螺旋线，其螺距用h表示，则有： hev.T-zomv, (12) 从(11)、(12)两式可以看出，电子运动的周期和螺距均与V,无关。虽然各个点 电子的径向速度不同，但由于轴向速度相同，由一点出发的电子束，经过一个周期以 后，它们又会在距离出发点相距一个螺距的地方重新相遇，这就是磁聚焦的基本原理， 由(12)式可得 e/m=8π2.V2/h2.Bi (13)

5 动的向心加速为 v / R 2 ，而产生这个加速度的力（有时称为向心力）必定为 m v / R 2  ， 所以圆弧的半径很容易计算出来。向心力等于 F  e  v B ，因而 m v / R e v B 2     即 R  mv / eB 。电子离开磁场区域之后，重新沿一条直线运动， 最后，电子束打在荧光屏上某一点，这一点相对于没有偏转的电子束的位置移动了一 段距离。 5．磁聚焦和电子荷质比的测量原理： 置于长直螺线管中的示波管，在不受任何偏转电压的情况下，示波管正常工作时， 调节亮度和聚焦，可在荧光屏上得到一个小亮点。若第二加速阳极 A2的电压为 V2 ， 则电子的轴向运动速度用 z v 表示，则有 m 2e V v 2 z   (9) 当给其中一对偏转板加上交变电压时，电子将获得垂直于轴向的分速度（用 r v 表 示），此时荧光屏上便出现一条直线，随后给长直螺线管通一直流电流 I ，于是螺线管 内便产生磁场，其磁场感应强度用 B 表示。众所周知，运动电子在磁场中要受到罗伦 磁力 F  evrB 的作用（ z v 方向受力为零），这个力使电子在垂直于磁场（也垂直于螺 线管轴线）的平面内作园周运动，设其园周运动的半径为 R ，则有： R m v e v B 2 r r     即 e B m v R r    (1 0) 圆周运动的周期为： e B 2 m v 2 R T r        (11) 电子既在轴线方面作直线运动，又在垂直于轴线的平面内作园周运动。它的轨道 是一条螺旋线，其螺距用 h 表示，则有： z vz e B 2 m h v T        (12) 从（11）、（12）两式可以看出，电子运动的周期和螺距均与 r v 无关。虽然各个点 电子的径向速度不同，但由于轴向速度相同，由一点出发的电子束，经过一个周期以 后，它们又会在距离出发点相距一个螺距的地方重新相遇，这就是磁聚焦的基本原理， 由（12）式可得 2 2 2 2 e / m  8  V / h  B (13)