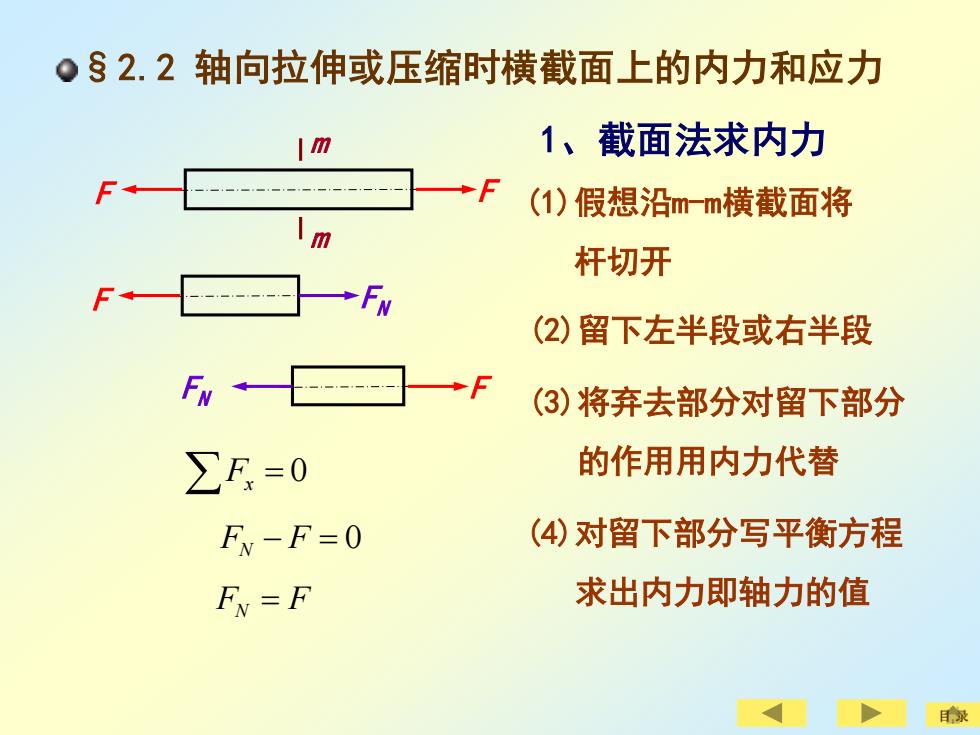
。§2.2轴向拉伸或压缩时横截面上的内力和应力 m 1、截面法求内力 ◆F (1)假想沿m-m横截面将 m 杆切开 →FW (2)留下左半段或右半段 Fw□→F (3)将弃去部分对留下部分 ∑F=0 的作用用内力代替 F-F=0 (4)对留下部分写平衡方程 FN=F 求出内力即轴力的值
§2.2 轴向拉伸或压缩时横截面上的内力和应力 1、截面法求内力 F F m m F FN Fx = 0 FN F FN − F = 0 FN = F 目 录 (1)假想沿m-m横截面将 杆切开 (2)留下左半段或右半段 (3)将弃去部分对留下部分 的作用用内力代替 (4)对留下部分写平衡方程 求出内力即轴力的值
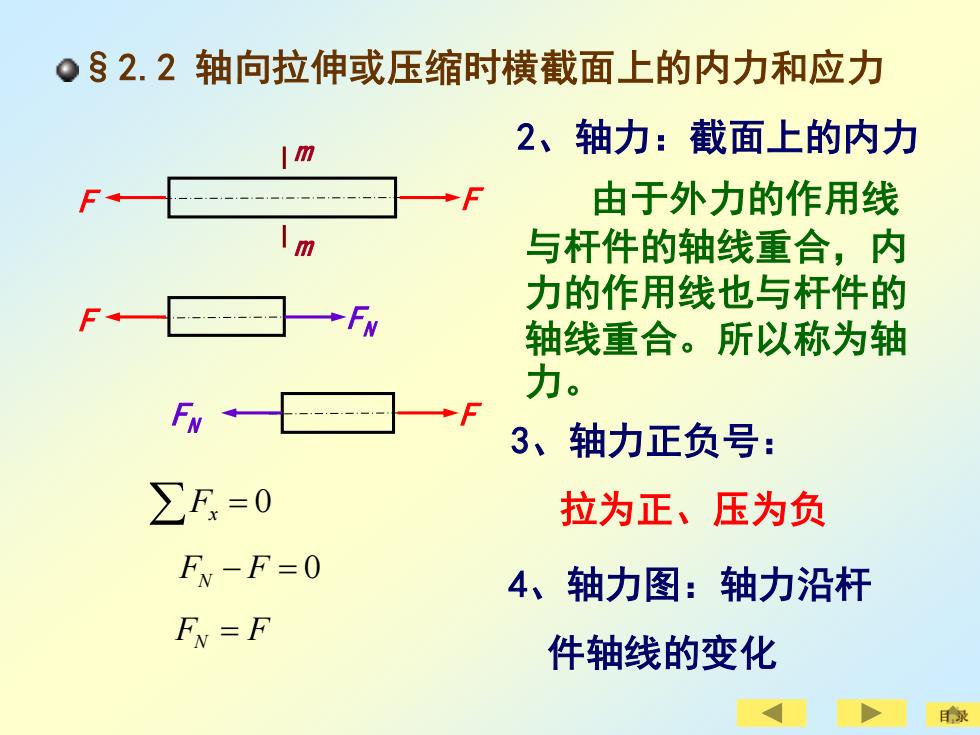
Q§2.2轴向拉伸或压缩时横截面上的内力和应力 m 2、轴力:截面上的内力 由于外力的作用线 m 与杆件的轴线重合,内 力的作用线也与杆件的 轴线重合。所以称为轴 力。 →F 3、轴力正负号: ∑F=0 拉为正、压为负 F-F=0 4、轴力图:轴力沿杆 FN=F 件轴线的变化
§2.2 轴向拉伸或压缩时横截面上的内力和应力 2、轴力:截面上的内力 Fx = 0 FN − F = 0 FN = F F F m m F FN FN F 目 录 由于外力的作用线 与杆件的轴线重合,内 力的作用线也与杆件的 轴线重合。所以称为轴 力。 3、轴力正负号: 拉为正、压为负 4、轴力图:轴力沿杆 件轴线的变化
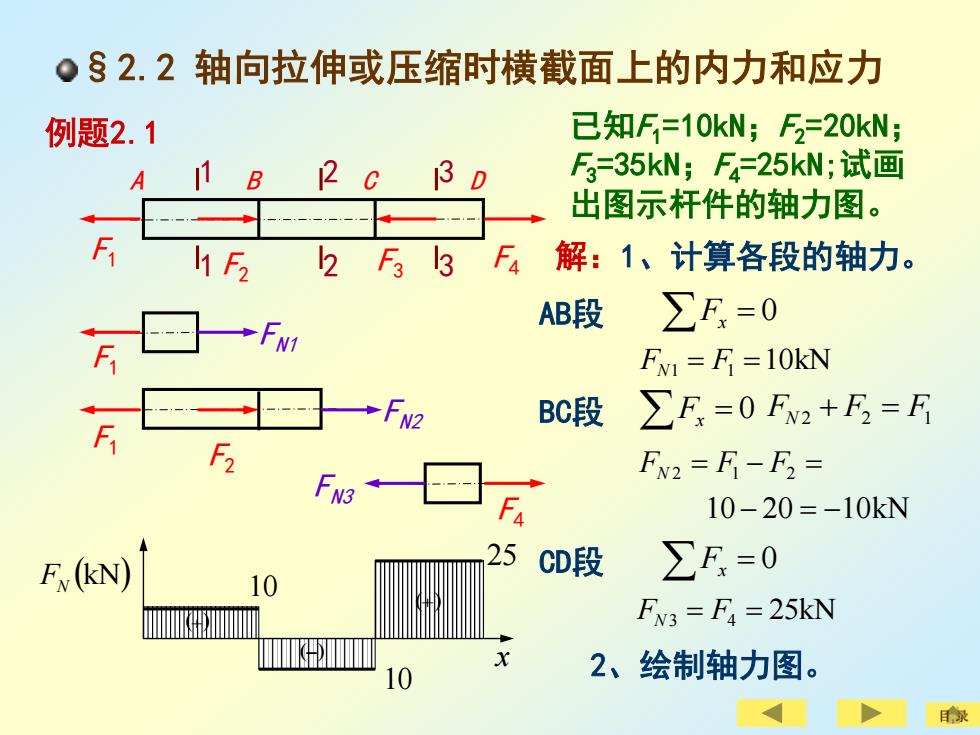
。§2.2轴向拉伸或压缩时横截面上的内力和应力 例题2.1 已知F=10kN;F=20N; 1B A 12 c 3D F3=35kN;F=25kN;试画 出图示杆件的轴力图。 F h F2 2F33F4解:1、计算各段的轴力。 AB段 ∑F=0 F FVI =F=10kN F →F2 BC段 ∑F=0FN2+F=F F2 FN2=F-F2= 10-20=-10kN 25 F (KkN) CD段 ∑F=0 10 F3=F4=25kN 2、绘制轴力图
§2.2 轴向拉伸或压缩时横截面上的内力和应力 已知F1=10kN;F2=20kN; F3=35kN;F4=25kN;试画 出图示杆件的轴力图。 1 1 例题2.1 FN1 F1 F1 F2 F3 F4 解:1、计算各段的轴力。 A B 2 C D 2 3 3 FN3 F4 FN2 F1 F2 Fx = 0 FN1 = F1 =10kN AB段 10 20 10kN 2 1 2 − = − FN = F − F = BC段 Fx = 0 FN2 + F2 = F1 Fx = 0 FN3 = F4 = 25kN CD段 2、绘制轴力图。 (kN) FN x 10 25 10 (+) (−) (+) 目 录

。§2.2轴向拉伸或压缩时横截面上的内力和应力 讨论题 1.以下关于轴力的说法中,哪一个是错误的 (A)拉压杆的内力只有轴力; (B)轴力的作用线与杆轴重合; (C)轴力是沿杆轴作用的外力; (D)轴力与杆的横截面和材料无关
§2.2 轴向拉伸或压缩时横截面上的内力和应力 目 录
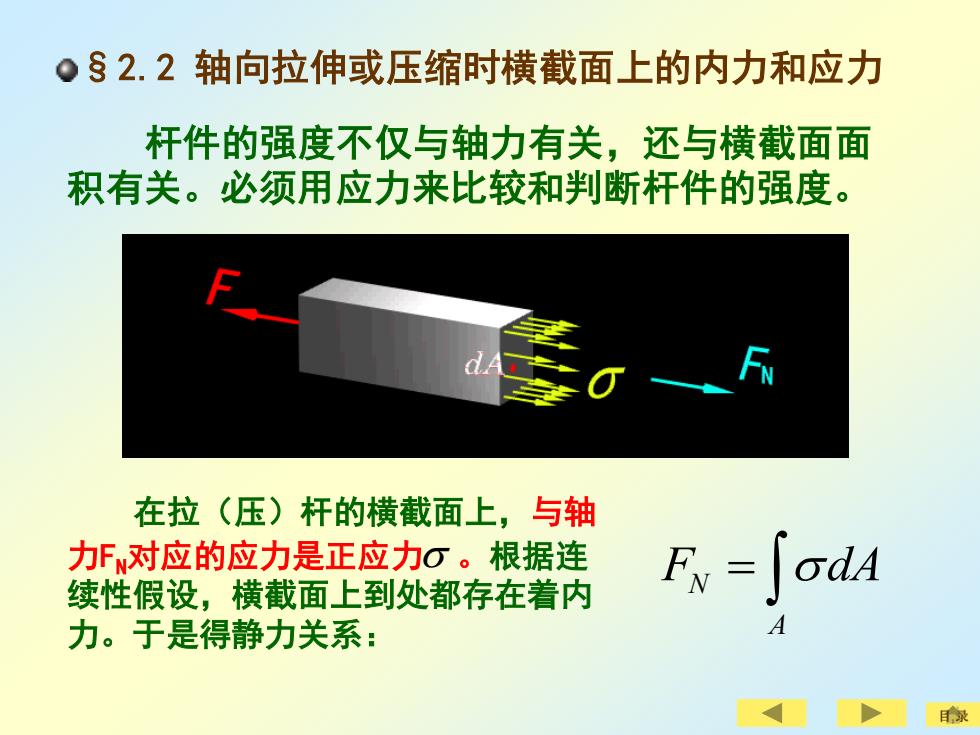
。§2.2轴向拉伸或压缩时横截面上的内力和应力 杆件的强度不仅与轴力有关,还与横截面面 积有关。必须用应力来比较和判断杆件的强度。 在拉(压)杆的横截面上,与轴 力F对应的应力是正应力O。根据连 续性假设,横截面上到处都存在着内 Fv=∫odA 力。于是得静力关系:
§2.2 轴向拉伸或压缩时横截面上的内力和应力 杆件的强度不仅与轴力有关,还与横截面面 积有关。必须用应力来比较和判断杆件的强度。 目 录 N A F dA = 在拉(压)杆的横截面上,与轴 力FN对应的应力是正应力 。根据连 续性假设,横截面上到处都存在着内 力。于是得静力关系: